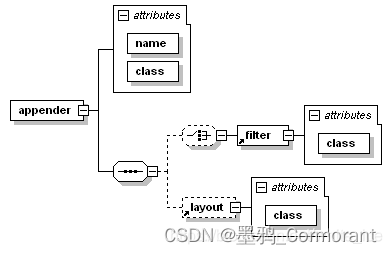
1. 核心函数solve
   一般形式 S=solve(eqns,vars,Name,Value) ，其中：

eqns是需要求解的方程组；

vars是需要求解的变量；

Name-Value对用于指定求解的属性（一般用不到）；

S是结果，对应于vars中变量；

2. 单个方程求解

方程：sin(x)=1

代码：

syms x; %定义x是一个未知量
eqn=sin(x)==1; % 定义方程，eqn只是一个代号，代表sin(x)==1
solX=solve(eqn,x) % 求方程eqn中的x，放入solX中

结果：

说明： MATLAB定义方程用的是 == 符号，就是这样规定的哈。

注意： 细心的同学应该发现了，本例的解实际上应该是 pi/2+2k*pi ，怎么得到呢？
添加Name-Value对即可解决，输入以下代码：

syms x; %定义x是一个未知量
eqn=sin(x)==1; % 定义方程，eqn只是一个代号，代表sin(x)==1
[solX,params,cond]=solve(eqn,x,'ReturnConditions',true) % 求方程eqn中x的所有解，放入solX中,params是参数，cond存储参数性质

得到理想结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8vvOBsvD-1686227552946)(2023-06-07-20-05-48.png)]

MATLAB 中求解方程和多元方程组可以使用 solve 函数。在求解方程时，需要将方程转化为形如 $f(x)=0$ 的函数形式，并进行输入。在求解多元方程组时，则需要将多个方程构成一个向量形式。

举一个简单的例子，假设我们要求解以下一元二次方程：

$$3x^2-4x+2=0$$

通过将方程移项可得到：

$$f(x)=3x^2-4x+2=0$$

我们可以直接将这个 $f(x)$ 函数输入 solve 函数进行求解：

% 定义方程
syms x;
eqn = 3*x^2 - 4*x + 2 == 0;% 求解方程
sol = solve(eqn,x);% 输出结果
disp(sol);

运行程序后，会输出方程的解：

sol =2^(1/2)/3 + 4/3-2^(1/2)/3 + 4/3

其中，最后一行输出了方程的两个根。

除此之外，在求解多元方程组时，也可以使用 solve 函数。例如，假设我们要求解以下多元方程组：

$$\{\begin{array}{l}2x+y-z=1\\ x-y+z=2\\ x+2y-3z=-1\end{array}$$

将方程组中的每个方程写成形如 $f(x_1,x_2,x_3)=0$ 的函数形式，并输入 solve 函数进行求解即可：

% 定义方程组
syms x y z;
eqn1 = 2*x + y - z == 1;
eqn2 = x - y + z == 2;
eqn3 = x + 2*y - 3*z == -1;% 求解方程组
[solx, soly, solz] = solve(eqn1, eqn2, eqn3, x, y, z);% 输出结果
disp(solx);
disp(soly);
disp(solz);

运行程序后，会输出方程组的三个变量的解。

需要注意的是，在使用 solve 函数时，需要将待求解的未知变量标记为符号类型 sym。同时，对于非线性方程或多元方程组， solve 函数可能无法找到精确解或者找到所有实数根，因此需要根据具体问题进行分析。

除了 solve 函数外，Matlab 中还提供了一些其他函数来求解方程和多元方程组。以下是一些常用的函数：

• fzero：用于求解一个非线性方程 $f(x)=0$ 的根。
• fsolve：用于求解一个多变量非线性方程组 $F(x_1,x_2,...,x_n)=0$ 的解。
• vpasolve：用于求解含有符号变量的方程或方程组的解，例如解析方程或微分方程等。

这些函数在用法上略有不同，但都可以解决方程和多元方程组的问题。下面以 fsolve 函数为例进行说明。

假设我们需要解以下的非线性方程组：

$$\{\begin{array}{l}{e}^y+x-10=0\\ x\sin (y)+y-3=0\end{array}$$

我们可以使用 fsolve 函数来求解该方程组的解。首先需要定义一个匿名函数，输入变量为一个列向量 $x=[x_1,x_2]$，输出变量为一个列向量 $F=[f_1(x_1,x_2),f_2(x_1,x_2)]$，即方程的左侧与右侧求差值的结果。

% 定义匿名函数
fun = @(x)[exp(x(2)) + x(1) - 10; x(1)*sin(x(2)) + x(2) - 3];% 定义初值
x0 = [0;0];% 求解方程组
[x,fval,exitflag] = fsolve(fun, x0);

其中，fun 函数定义了方程组的左侧和右侧之间的差值，x0 是变量的一个初值， fsolve 函数将通过迭代来寻找合适的解。结果包括求解出来的变量值 x，方程组的残差 fval 和退出标志 exitflag。查阅文档可以了解各个退出标志的含义。

需要注意的是，对于非线性方程或多元方程组的求解，可能会出现无法求解或求解不唯一的情况，因此需要根据具体问题进行分析。

除了 fsolve 函数外，Matlab 中还提供了一些其他求解方程和多元方程组的函数。以下是一些常用的函数：

• roots：求解一个多项式方程 $f(x)={\sum }_{i=0}^n{a}_i{x}^i$ 的根。
• polyfit 和 polyval 组合：用于拟合数据，并返回相应的多项式系数。
• ode45：求解常微分方程问题。

这些函数的使用方法和注意事项可以在 Matlab 官方文档中查看。需要注意的是，在求解各种类型的方程和多元方程组时，需要综合考虑模型的适用性、精度与效率等因素，以得到最好的结果。

1. 带未知参数的方程
   方程： ax²+bx+c=0
   代码：

syms x a b c; %定义x a b c是未知量
eqn=a*x^2+b*x+c==0;% 定义方程
solX=solve(eqn,x) % 解方程

结果：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JU3I5asH-1686563889619)(2023-06-07-20-06-08.png)]
说明： 这里就简单的把未知参数用syms声明就可以了。

1. 多元方程组求解
   方程：

代码：

syms u v; % 定义u v 是未知量
eqns=[2*u+v==0,u-v==1]; % 定义方程组
vars=[u,v]; % 定义求解的未知量
[solU,solV]=solve(eqns,vars) % 求解eqns中的vars未知量，分别存储
sol=solve(eqns,vars); % 求解eqns中的vars未知量，以结构体的形式存储到sol中
solU1=sol.u % 从sol结构体中取出变量u的解
solV1=sol.v % 从sol结构体中取出变量v的解

结果：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4t7C6TKY-1686563889620)(2023-06-07-20-07-10.png)]

说明： 本例中有两个求解的变量，有两种存储方式，已在代码中介绍。

1. 数值近似解
   方程： sin(x)==x²-1
   代码：

syms x; % 定义x是未知量
fplot(sin(x),[-2,2]); % 绘制y=sin(x)的图像
hold on; 
fplot(x^2-1,[-2,2]); % 绘制y=x^2-1的图像
hold off;
eqn=sin(x)==x^2-1; % 定义方程
solX=solve(eqn,x) % 直接求解，返回其找到的第一个数值近似解
solX1=vpasolve(eqn,x,[0,2]) % vpa求解，返回其在范围[0,2]内找到的第一个数值近似解

结果：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vbsvsdzS-1686563889620)(2023-06-07-20-07-22.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Q9SsTVYR-1686563889621)(2023-06-07-20-07-28.png)]

说明： 此例中无法求得精确解，slove会返回求得的第一个数值近似解，vpasolve可以返回指定范围内第一个近似解

1. 无解的情况

方程：

代码：

syms x; % 定义x是未知量
eqn=[3*x+2==0,3*x+1==0]; % 定义函数
solX=solve(eqn,x) % 求解

结果：