【Python】新鲜出炉的海洋捕食者算法Python版本-编程知识

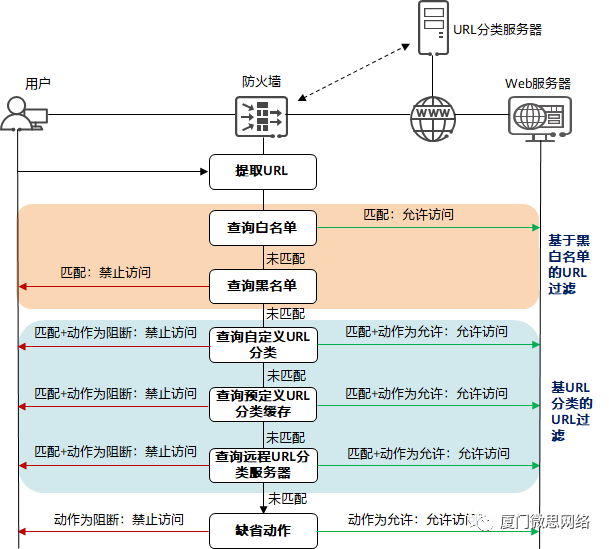
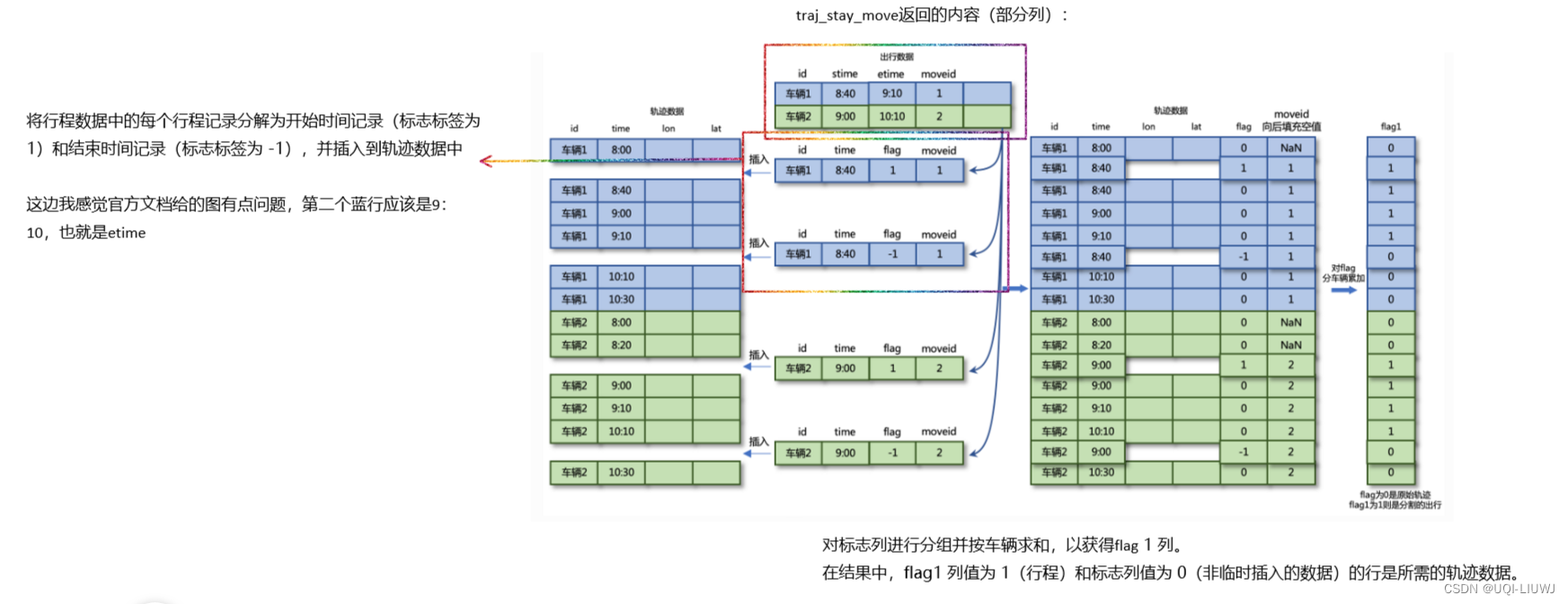
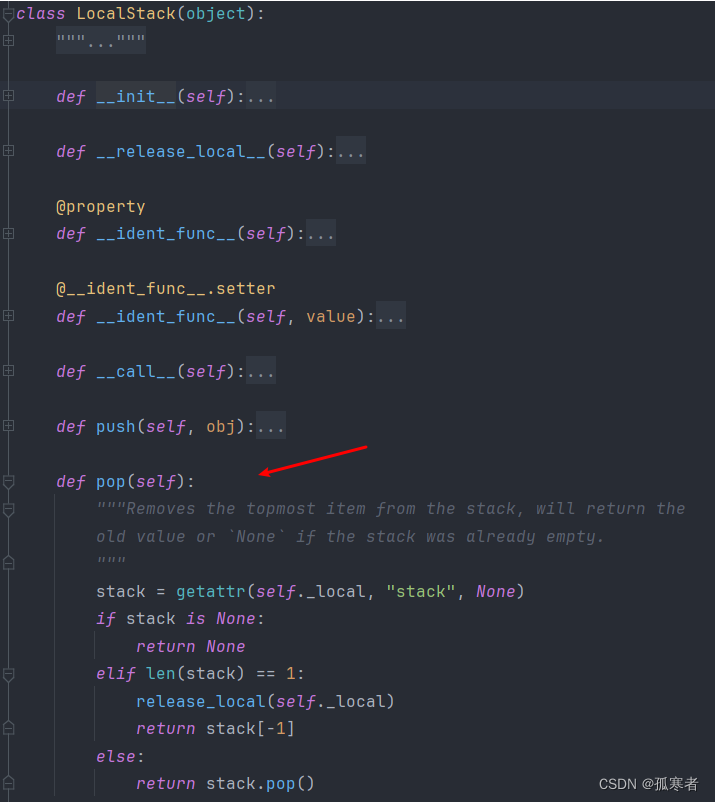
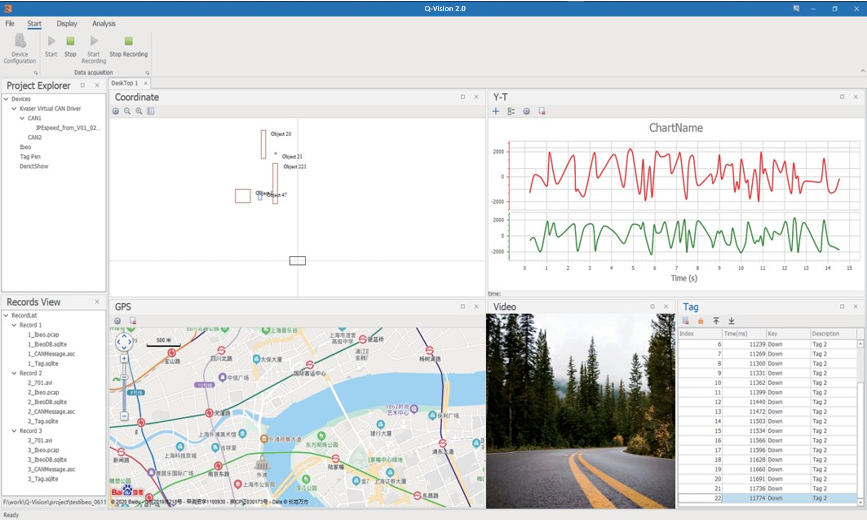
2020年发表的海洋捕食者算法《Marine Predators Algorithm: A nature-inspired metaheuristic》。

作者只在原论文中给出了MATLAB代码，网上也没有Python版本，我自己用Python重写了MATLAB代码。

"""2020海洋捕食者算法
"""
import numpy as np
import random
import mathdef initial(pop, dim, ub, lb):X = np.zeros([pop, dim])for i in range(pop):for j in range(dim):X[i, j] = random.random() * (ub[j] - lb[j]) + lb[j]  # 均匀分布随机初始化return X, lb, ub# 将超过边界的直接用边界值赋值
def BorderCheckForOne(x, ub, lb, pop, dim):if x > ub[0]:x = ub[0]elif x < lb[0]:x = lb[0]return xdef levy(n, m, beta):num = math.gamma(1+beta)*math.sin(math.pi*beta/2)den = math.gamma((1+beta)/2) * beta * 2**((beta-1)/2)sigma_u = (num/den)**(1/beta)u = np.random.normal(0,sigma_u,(n,m))v = np.random.normal(0,1,(n,m))return u/(np.abs(v)**(1/beta)) ## ^的用法好像有错def MPA(pop, dim, lb, ub, MaxIter, fun):Top_predator_pos = np.zeros(dim)  #或者np.zeros([1,dim])Top_predator_fit = float("inf")Convergence_curve = np.zeros(MaxIter)stepsize = np.zeros([pop, dim])  # pop×dimfitness = np.inf * np.ones([pop, 1])   # pop×1# 初始化种群X, lb, ub = initial(pop, dim, ub, lb)Xmin = lb[0] * np.ones([pop, dim])Xmax = ub[0] * np.ones([pop, dim])Iter = 0FADs = 0.2P = 0.5while Iter < MaxIter:# =================== 对上一轮的进行复盘 ============for i in range(0, pop):# 1.边界检测for j in range(0, dim):X[i, j] = BorderCheckForOne(X[i, j], ub, lb, pop, dim)# 2.计算每个鲨鱼的适应度值fitness[i, 0] = fun(X[i, :])if fitness[i, 0] < Top_predator_fit:  # 23个基准函数都是越小越好Top_predator_fit = fitness[i, 0].copy()Top_predator_pos = X[i, :].copy()# =================== Memory saving ===============if Iter == 0:fit_old = fitness.copy()X_old = X.copy()for i in range(pop):if fit_old[i, 0] < fitness[i, 0]:fitness[i, 0] = fit_old[i, 0].copy()  # 如果上一轮的位置更好，还是用上一轮的X[i, :] = X_old[i, :].copy()fit_old = fitness.copy()X_old = X.copy()# =================== Levy=======Elite = np.ones([pop, 1]) * Top_predator_posCF = (1-Iter/MaxIter)**(2*Iter/MaxIter)RL=0.05*levy(pop, dim, 1.5)  # levy返回一个pop×dim的矩阵RB = np.random.randn(pop, dim)  # 满足正态分布的pop×dim大小矩阵# ===============遍历每个个体==============for i in range(pop):for j in range(dim):R = random.random()# ================公式12============if Iter < MaxIter/3:stepsize[i, j] = RB[i, j] * ( Elite[i, j]-RB[i, j]*X[i, j] )X[i, j] = X[i, j] + P*R*stepsize[i, j]# ===============公式13 和 14=======elif Iter>MaxIter/3 and Iter < 2*MaxIter/3:if i > pop/2:stepsize[i, j] = RB[i, j] * (RB[i, j]*Elite[i, j]-X[i, j])X[i, j] = Elite[i, j] + P*CF*stepsize[i, j]else:stepsize[i, j] = RL[i, j] * (Elite[i, j]-RL[i, j]*X[i, j])X[i, j] = X[i, j] + P * R *stepsize[i, j]# ==============公式15==============else:stepsize[i, j] = RL[i, j]*( RL[i, j]*Elite[i, j]-X[i, j])X[i, j] = Elite[i, j] + P*CF*stepsize[i, j]# =================== 对上一轮的进行复盘 ============for i in range(0, pop):# 1.边界检测for j in range(0, dim):X[i, j] = BorderCheckForOne(X[i, j], ub, lb, pop, dim)# 2.计算每个鲨鱼的适应度值fitness[i, 0] = fun(X[i, :])if fitness[i, 0] < Top_predator_fit:  # 23个基准函数都是越小越好Top_predator_fit = fitness[i, 0].copy()Top_predator_pos = X[i, :].copy()# =================== Memory saving ===============if Iter == 0:fit_old = fitness.copy()X_old = X.copy()for i in range(pop):if fit_old[i, 0] < fitness[i, 0]:fitness[i, 0] = fit_old[i, 0].copy()  # 如果上一轮的位置更好，还是用上一轮的X[i, :] = X_old[i, :].copy()fit_old = fitness.copy()X_old = X.copy()# =====================对整体进行一个更新（公式16）=====if random.random() < FADs:U = (np.random.rand(pop, dim) < FADs)X = X + CF*np.multiply(Xmin + np.multiply(np.random.rand(pop, dim), (Xmax-Xmin)), U)else:r = random.random()stepsize = (FADs*(1-r)+r) * (X[random.sample(range(0, pop), pop),:] - X[random.sample(range(0, pop), pop),:])X = X + stepsizeIter = Iter+1if Iter!=MaxIter:Convergence_curve[Iter] = Top_predator_fitreturn Top_predator_fit, Top_predator_pos, Convergence_curve

在23个基准函数上跑了一遍，验证得代码正确

fun 1 ---- 4 轮的平均值: 1.590879014464718e-22
fun 2 ---- 4 轮的平均值: 3.1015801972813803e-13
fun 3 ---- 4 轮的平均值: 2.1687101928786233e-05
fun 4 ---- 4 轮的平均值: 2.738516688049143e-09
fun 5 ---- 4 轮的平均值: 24.3651022631242
fun 6 ---- 4 轮的平均值: 1.5518969799868655e-08
fun 7 ---- 4 轮的平均值: 0.0007603777498045276
fun 8 ---- 4 轮的平均值: -9759.428902632117
fun 9 ---- 4 轮的平均值: 0.0
fun 10 ---- 4 轮的平均值: 1.1923795284474181e-12
fun 11 ---- 4 轮的平均值: 0.0
fun 12 ---- 4 轮的平均值: 9.427489581332269e-10
fun 13 ---- 4 轮的平均值: 2.018121184109257e-08
fun 14 ---- 4 轮的平均值: 0.9980038377944498
fun 15 ---- 4 轮的平均值: 0.00030748598780886593
fun 16 ---- 4 轮的平均值: -1.0316284534898776
fun 17 ---- 4 轮的平均值: 0.39788735772973816
fun 18 ---- 4 轮的平均值: 2.999999999999924
fun 19 ---- 4 轮的平均值: -3.862782147820756
fun 20 ---- 4 轮的平均值: -3.3219951715813822
fun 21 ---- 4 轮的平均值: -10.153199679022137
fun 22 ---- 4 轮的平均值: -10.40294056677283
fun 23 ---- 4 轮的平均值: -10.53640981666291