2024年阿里云服务器地域分布表,地域指数据中心所在的地理区域,通常按照数据中心所在的城市划分,例如华北2(北京)地域表示数据中心所在的城市是北京。阿里云地域分为四部分即中国、亚太其他国家、欧洲与美洲和中东,参考 https://t.aliyun.com/U/bLynLC 如下图:

阿里云服务器地域2024年分布表
关于地域的选择,请参考:阿里云服务器地域和可用区选择方法(看这一篇就够了)
- 亚太中国:华北1(青岛)、华北2(北京)、华北3(张家口)、华北5(呼和浩特)、华北6(乌兰察布)、华东1(杭州)、华东2(上海)、华东5(南京)、华东6(福州)、华南1(深圳)、华南2(河源)、华南3(广州)、西南1(成都)、中国(香港)、华中1(武汉)
- 亚太其他国家:日本(东京)、韩国(首尔)、新加坡、澳大利亚(悉尼)、马来西亚(吉隆坡)、菲律宾(马尼拉)、印度尼西亚(雅加达)、印度(孟买)、泰国(曼谷)
- 欧洲与美洲:美国(弗吉尼亚)、美国(硅谷)、英国(伦敦)、德国(法兰克福)
- 中东:阿联酋(迪拜)
阿里云服务器地域和可用区详细分布表
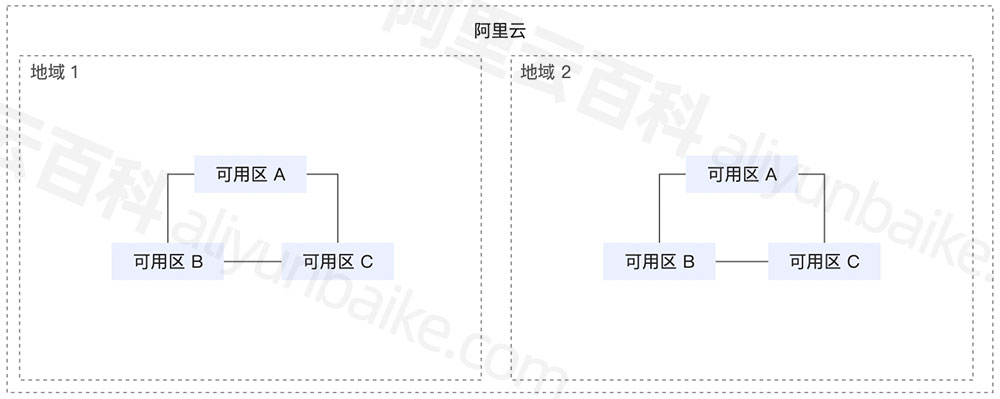
2024年更新阿里云服务器地域和可用区分布
中国地区地域节点和可用区:
| 地域名称 | 地域ID | 可用区数量 | 可用区名称 |
|---|---|---|---|
| 华北1(青岛) | cn-qingdao | 2 |
|
| 华北2(北京) | cn-beijing | 12 |
|
| 华北3(张家口) | cn-zhangjiakou | 3 |
|
| 华北5(呼和浩特) | cn-huhehaote | 2 |
|
| 华北6(乌兰察布) | cn-wulanchabu | 3 |
|
| 华东1(杭州) | cn-hangzhou | 8 |
|
| 华东2(上海) | cn-shanghai | 11 |
|
| 本地地域) | cn-nanjing | 1 | 南京-本地地域 可用区A |
| 华东6(福州-本地地域) | cn-fuzhou | 1 | 福州-本地地域 可用区A |
| 华中1(武汉-本地地域) | cn-wuhan-lr | 1 | 武汉-本地地域 可用区A |
| 华南1(深圳) | cn-shenzhen | 6 |
|
| 华南2(河源) | cn-heyuan | 2 |
|
| 华南3(广州) | cn-guangzhou | 2 |
|
| 西南1(成都) | cn-chengdu | 2 |
|
| 中国香港 | cn-hongkong | 3 |
|
其他国家和地区:
| 地域名称 | 地域ID | 可用区数量 | 可用区名称 |
|---|---|---|---|
| 新加坡 | ap-southeast-1 | 3 |
|
| 澳大利亚(悉尼) | ap-southeast-2 | 2 |
|
| 马来西亚(吉隆坡) | ap-southeast-3 | 2 |
|
| 印度尼西亚(雅加达) | ap-southeast-5 | 3 |
|
| 菲律宾(马尼拉) | ap-southeast-6 | 1 | 马尼拉 可用区A |
| 泰国(曼谷) | ap-southeast-7 | 1 | 曼谷 可用区A |
| 印度(孟买) | ap-south-1 | 2 |
|
| 日本(东京) | ap-northeast-1 | 3 |
|
| 韩国(首尔) | ap-northeast-2 | 1 | 首尔 可用区A |
| 美国(硅谷) | us-west-1 | 2 |
|
| 美国(弗吉尼亚) | us-east-1 | 2 |
|
| 德国(法兰克福) | eu-central-1 | 3 |
|
| 英国(伦敦) | eu-west-1 | 2 |
|
| 阿联酋(迪拜) | me-east-1 | 1 | 迪拜 可用区A |
| 沙特(利雅得-合作伙伴运营) | me-central-1 | 2 | 利雅得-合作伙伴运营 可用区A利雅得-合作伙伴运营 可用区B |
更多关于阿里云服务器地域分布,请参考官方页面:https://t.aliyun.com/U/X1G8iT



![[足式机器人]Part2 Dr. CAN学习笔记-Advanced控制理论 Ch04-16 Robust Controller非线性鲁棒控制器](https://img-blog.csdnimg.cn/direct/9026a8987f9b414d9772e76295c168bc.png#pic_center)