1.数据集制作思路(生成用于拟合金融趋势图像的分段线性函数)
那么如何去制作这样的一个类minist的金融趋势曲线数据集呢?
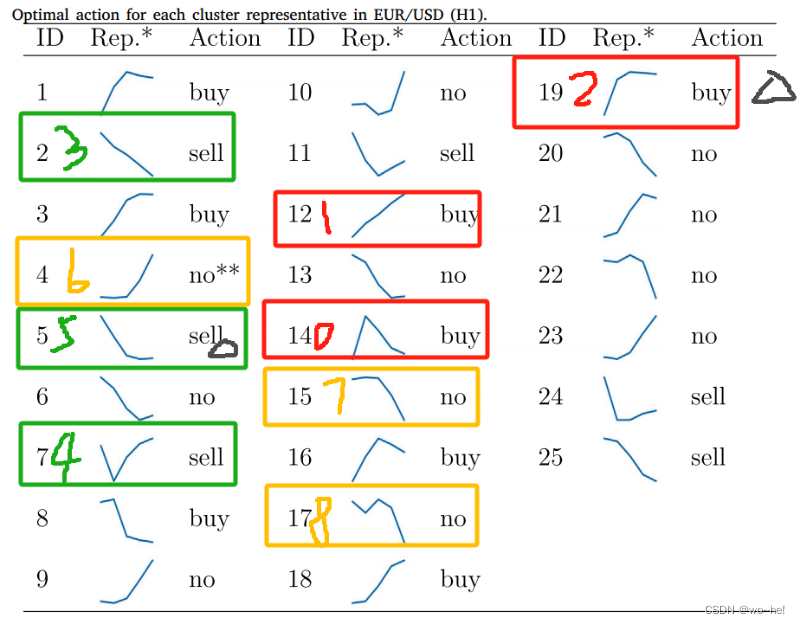
还是如上图所示,为了使类别平均分布,因此可以选取三种“buy”的曲线、三种“sell”的曲线以及三种“no”的曲线来作为新数据集的基本数据类别。那么buy类别的曲线可以选取上图中的第14、12、19个图像,并将其主标签类别设为0、1、2;那么sell类别的曲线可以选取上图中的第2、5、7个图像,并将其主标签类别设为3、4、5;那么no类别的曲线可以选取上图中的第4、15、18个图像,并将其主标签类别设为6、7、8。
选好标签后,就是考虑如何去拟合它们。我们发现选取的这些图片都各有千秋。比如第2个表示“sell”的图,其实可以直接用y=-kx进行拟合,只是调整它的斜率(k>0)即可。第12、25张图也同理。而像第4张图,它其实可以用两段分段线性函数去拟合(当然你也可以去使用多段线性函数去拟合它,我这里为了偷懒就说两段吧。而且还有一个原因就是无论你是两段还是更多段,在你把它转为28*28的像素图片后其实里面的细节不太容易看出来,所以我觉得两段就行。)如下图所示,前一段可以用y=±kx表示,而后一段可以使用y=kx(k>0)表示,分别随机调整它们的斜率就能生成无数种类似图片。第1、3、4、5、6、7、9、11、14、15、16、19、20、23、24张图也同理。而剩下没有提到的图片我认为可以使用三段线性函数去进行拟合,因为以17举例,它包括了一段降、一段升和一段降的趋势,也主要是这三种趋势会提示网络不进行买卖的操作。

有了上面的思路后就好说了,以生成第14张图为例,直接上代码,下面这段代码不光把第14张图的曲线拟合出来了,还对生成的图像进行了黑底白线的处理。且生成的图像的两段的斜率是随机的,从而保证能够生成若干张图片来形成数据集。
import matplotlib.pyplot as plt
import numpy as np
import randomt1 = np.arange(-4, 0, 0.01)#分段函数的定义域与精度
t2 = np.arange(0, 2, 0.01)# print(random.randint(pre_data0,99))
y1_list = [] # 记录函数值
y2_list = [] # 记录函数值
number = 50
def y(t1,t2):t1 = t1 * random.uniform(1,5) # t1 * 随机的斜率kt2 = t2 * random.uniform(1,5)for i in t1:y1_list.append(i)for j in t2:y2_list.append(-j)num=6000 #需要制造的数据量
for j in range(num):y1_list = []y2_list = []y(t1, t2)#调整画布背景颜色为黑色ax = plt.axes().set_facecolor('black')#根据函数画出来的曲线是白色,并且稍粗一些plt.plot(t1, y1_list, linewidth = 3.0, color='white')plt.plot(t2, y2_list, linewidth = 3.0, color='white')#去横纵坐标ax = plt.subplot()ax.set_xticks([])ax.set_yticks([])#去图片边框plt.subplots_adjust(top=1, bottom=0, right=1, left=0, hspace=0, wspace=0)plt.margins(0, 0)#用于放大缩小图像plt.xlim(-5, 3) # 坐标轴范围plt.ylim(-8, 1)plt.savefig('./pre_data0/{}_0.jpg'.format(j+1))plt.show()