Java数据结构之图(头歌平台，详细注释)-编程知识

第1关：图的表示

任务描述

图（Graph）是表示一些事物或者状态的关系的表达方法。由于许多问题都可以归约为图的问题，人们提出了许多和图相关的算法。

本关任务：学习图的相关概念和表示，并用邻接表示图。

相关知识

图是什么

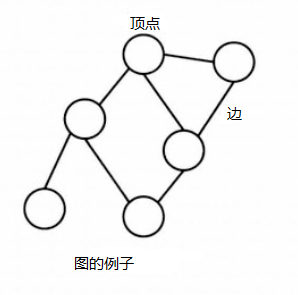
图由顶点（Vertex）和边（Edge）组成。顶点代表对象。在画示意图的时候，我们使用点或圆圈来表示顶点。边表示的是两个对象的连接关系。在示意图中，我们使用连接顶点之间的线段来表示。顶点的集合是V、边的集合是E的图记为G=(V, E)，连接两点u和v的边用e=(u, v)表示。

图的种类

图大体上分为2种。边没有指向性的图叫做无向图，边具有指向性的图叫做有向图。

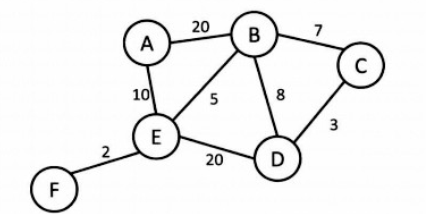
我们可以给边赋予各种各样的属性。比较具有代表性的有权值（cost）。边上带有权值的图叫带权图。在不同问题中，权值可以代表距离、时间以及价格等不同的属性。如下图所示的带权图。

无向图的术语

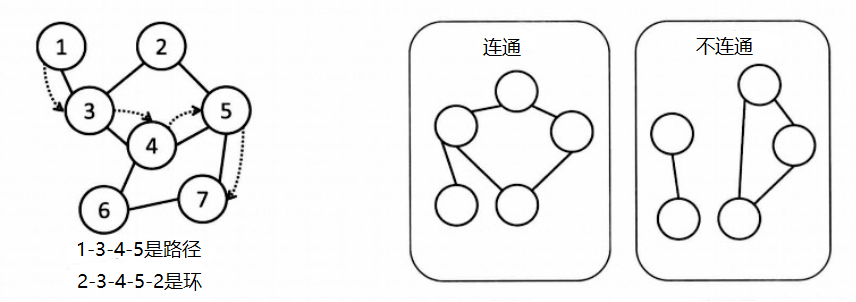
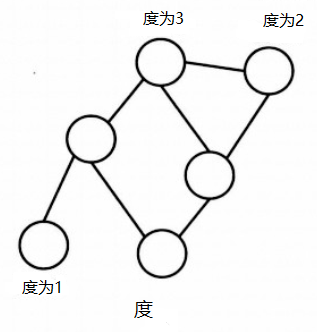
对于无向图，如果两个顶点之间有边连接，那么就视为两个顶点相邻。相邻顶点的序列称为路径。起点和终点重合的路径叫做环。任意两点之间都有路径连接的图叫做连通图。顶点连接的边数叫做这个顶点的度。

没有环的连通图叫做树（tree），没有环的非连通图叫做森林。一棵树的边数恰好是顶点数减1。反之，边数等于顶点数减1的连通图就是一棵树。

有向图的术语

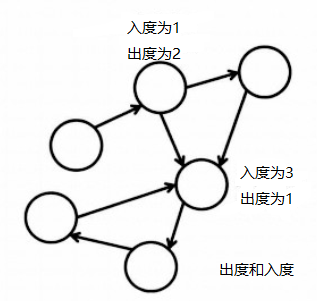
在有向图中，以顶点v为起点的边的数量称为v的出度，以v为终点的边的数量称为v的入度。

图的表示

为了能在程序中对图进行处理，需要用具体的数据结构存储顶点和边。在图的表示方法中，代表性的存储方法有邻接矩阵和邻接表。我们把顶点和边的集合记为V和E，|V|和|E|分别表示顶点和边的数量。

邻接矩阵

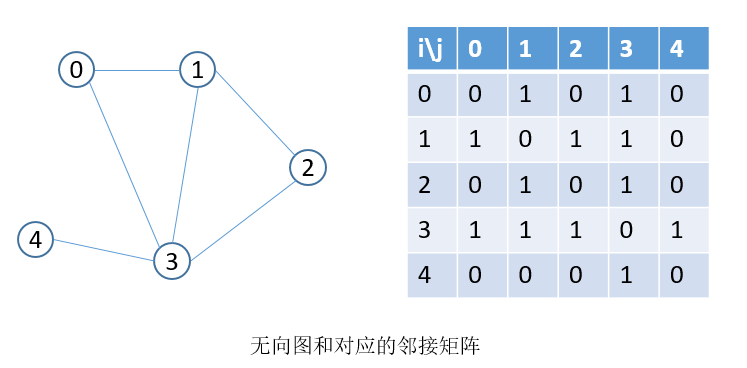
邻接矩阵使用大小为|V|×|V|的二维数组G来表示图。G[i][j]表示的是顶点i和顶点j的关系。

无向图中，只需知道“顶点i和顶点j之间是否有边连着”这样的信息，因此，如果顶点i和顶点j之间有边相连，那么G[i][j]和G[j][i]就设为1，否则设为0。

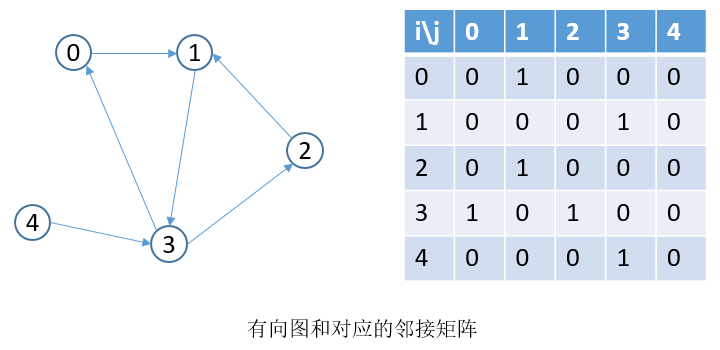
有向图中，只需知道“是否有从顶点i指向顶点j的边”这样的信息，因此，如果顶点i有一条指向顶点j的边，那么G[i][j]设为1，否则设为0。

有向图与无向图不同，并不满足G[i][j]=G[j][i]。

邻接表

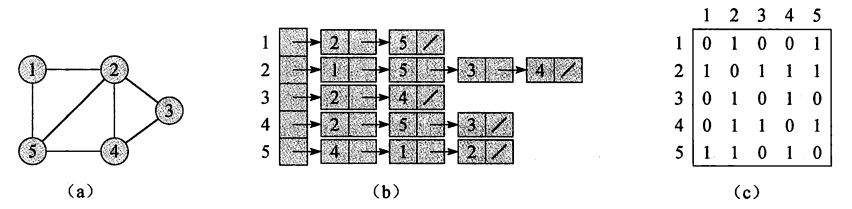
邻接表，是通过把“从顶点1出发有到顶点2, 5的边”这样的信息保存在链表中来表示图的。即如果从顶点1到顶点2之间有边，则把顶点2添加到顶点1的邻接表中。具体请参考下图。

下面是两种表示的一个示例。

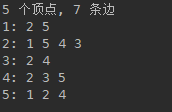
无向图的两种表示。(a)一个有5个顶点和7条边的无向图G。(b) G的邻接表表示。(c) G的邻接矩阵表示。

有向图的两种表示。(a)一个有6个顶点和8条边的有向图G。(b) G的邻接表表示。(c) G的邻接矩阵表示。

package step1;import java.util.ArrayList;public class Graph {private int V;//顶点数private int E;//边数private ArrayList<Integer>[] adj;//邻接表public Graph(int v) {if (v < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");V = v;E = 0;adj = new ArrayList[V + 1];for (int i = 0; i <= this.V; i++) {adj[i] = new ArrayList<Integer>();}}public void addEdge(int v, int w) {/********** Begin *********///邻接表adj[v].add(w);//v连接wadj[w].add(v);//w连接vE++;//增加一条边/********** End *********/}public String toString() {StringBuilder s = new StringBuilder();s.append(V + " 个顶点, " + E + " 条边\n");for (int v = 1; v <= V; v++) {s.append(v + ": ");for (int w : adj[v]) {s.append(w + " ");}s.append("\n");}return s.toString();}
}

以下是测试样例：

测试输入： 5 7 1 2 1 5 2 5 2 4 2 3 3 4 4 5 （第一行中的5和7分别表示顶点数和边数，不会作为函数addEdge()的参数传入。）

预期输出：

第2关：深度优先搜索

任务描述

像遍历树的结点那样，按照特定顺序访问图的所有顶点的算法就是图的搜索（search）算法。图的搜索过程中，利用哪些边，以何种顺序访问顶点等信息可以帮助我们分析出图的结构。

本关任务：实现深度优先搜索。

相关知识

深度优先搜索介绍

图的深度优先搜索(Depth-First Search，DFS)，是找出图结构所有顶点的最简单最传统的方法。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

深度优先搜索图解

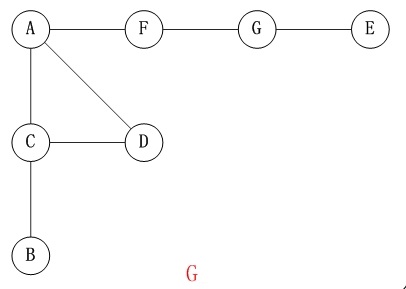
下面以无向图来对深度优先搜索进行图示。

对上面的图G进行深度优先搜索，从顶点A开始。

第1步：访问A。

第2步：访问(A的邻接点)C。（在第1步访问A之后，接下来应该访问的是A的邻接点，即C, D, F中的一个。这里访问的是C）

第3步：访问(C的邻接点)B。 (在第2步访问C之后，接下来应该访问C的邻接点，即B和D中一个(A已经被访问过，就不算在内)。这里访问B。）

第4步：访问(C的邻接点)D。 (在第3步访问了C的邻接点B之后，B没有未被访问的邻接点；因此，返回到访问C的另一个邻接点D。)

第5步：访问(A的邻接点)F。（前面已经访问了A，并且访问完了A的邻接点C的所有邻接点(包括递归的邻接点在内)；因此，此时返回到访问A的另一个邻接点F。

第6步：访问(F的邻接点)G。

第7步：访问(G的邻接点)E。

因此访问顺序是：A -> C -> B -> D -> F -> G -> E

package step2;import java.util.ArrayList;public class DFSGraph {private boolean[] marked;private int V;//顶点数private int E;//边数private ArrayList<Integer>[] adj;//邻接表public DFSGraph(int v) {if (v < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");V = v;E = 0;adj = new ArrayList[V + 1];marked = new boolean[V + 1];for (int i = 0; i <= this.V; i++) {adj[i] = new ArrayList<Integer>();}}public void addEdge(int v, int w) {adj[v].add(w);adj[w].add(v);E++;}public void DFS(int v) {/********** Begin *********/if(marked[v]){//如果已经被标记则代表找过，直接返回return;}marked[v] = true;//没被标记则改为true，表示被标记System.out.print(v + " ");//输出被遍历的点for (int w : adj[v]) {//遍历adj集合中v连接的元素w，将每次遍历的元素赋值给w取出每一个元素if (!marked[w]) {//如果没有被标记则进入DFS(w);//递归往下继续找}}/********** End *********/}public String toString() {StringBuilder s = new StringBuilder();s.append(V + " 个顶点, " + E + " 条边\n");for (int v = 1; v <= V; v++) {s.append(v + ": ");for (int w : adj[v]) {s.append(w + " ");}s.append("\n");}return s.toString();}
}

测试输入：

5 7 1 2 1 5 2 5 2 4 2 3 3 4 4 5 （第一行5和7表示顶点数和边数）

预期输出：

第3关：广度优先搜索

任务描述

本关介绍另一种图搜索算法————广度优先搜索法（Breadth First Search，BFS）。与深度搜索法一样，广度优先搜索法也得到广泛应用。广度优先搜索与深度优先搜索相互配合，就能形成图搜索方式的两个轴。

本关任务：实现图的广度优先搜索。

相关知识

深度优先搜索的过程并不直观，而广度优先搜索的过程理解起来非常容易。因为，广度优先搜索法从离起点最近的顶点开始按顺序访问。

广度优先搜索介绍

广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2...的顶点。

广度优先搜索图解

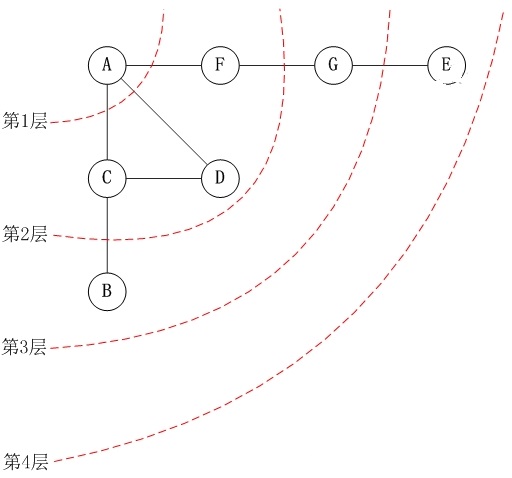
下面以"无向图"为例，来对广度优先搜索进行图示。

对上面的图G进行广度优先搜索，从顶点A开始。

第1步：访问A。

第2步：依次访问A的邻接点C，D，F。（在第2步访问完C，D，F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再访问F的邻接点G。）

第3步：依次访问B，G。（在第3步访问完B，G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻接点E。）

第4步：访问E。因此访问顺序是：A -> C -> D -> F -> B -> G -> E。

package step3;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;public class BFSGraph {private int V;//顶点数private int E;//边数private boolean[] marked;private ArrayList<Integer>[] adj;//邻接表public BFSGraph(int v) {if (v < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");V = v;E = 0;adj = new ArrayList[V + 1];marked = new boolean[V + 1];for (int i = 0; i <= this.V; i++) {adj[i] = new ArrayList<Integer>();}}public void addEdge(int v, int w) {adj[v].add(w);adj[w].add(v);E++;}public void BFS(int s) {/********** Begin *********/Queue<Integer> q = new LinkedList<Integer>();//定义一个队列q.add(s);//将顶点入队marked[s] = true;//标记入队顶点while (!q.isEmpty()) {//如果队列不为空int v = q.poll();//取出最先入队的顶点System.out.print(v + " ");//输出该顶点for (int w:adj[v]) {//遍历adj集合中v连接的元素w，将每次遍历的元素赋值给w取出每一个元if (!marked[w]) {//没被标记则进入q.add(w);//将该点入队marked[w] = true;//标记该点}}}/********** End *********/}public String toString() {StringBuilder s = new StringBuilder();s.append(V + " 个顶点, " + E + " 条边\n");for (int v = 1; v <= V; v++) {s.append(v + ": ");for (int w : adj[v]) {s.append(w + " ");}s.append("\n");}return s.toString();}
}

测试输入：

6 8 1 2 1 3 1 6 2 3 3 4 3 5 4 5 4 6 （6和8表示顶点数和边数）

预期输出：

第4关：单源最短路径

任务描述

在图的应用中，有一个很重要的需求：我们需要知道从某一个点开始，到其他所有点的最短路径。这其中，Dijkstra算法是典型的最短路径算法。

本关任务：实现Dijkstra算法求单源最短路径。

相关知识

Dijkstra算法

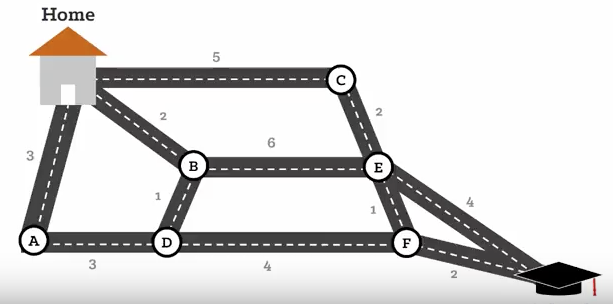
迪杰斯特拉算法（Dijkstra's algorithm）是由荷兰计算机科学家Edsger Wybe Dijkstra提出。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

在下图中找到从家到学校的最短路径：

(可以使用Dijkstra算法找到的最短路径是 Home->B->D->F->School)

基本思想：

将图G中所有的顶点V分成两个顶点集合S和T。以v为源点已经确定了最短路径的终点并入S集合中，S初始时只含顶点v,T则是尚未确定到源点v最短路径的顶点集合。然后每次从T集合中选择S集合点中到T路径最短的那个点，并加入到集合S中，并把这个点从集合T删除。直到T集合为空为止。

算法步骤：

初始时，S只包含源点，即S＝{v}，v的距离为0。T包含除v外的其他顶点，即:T={其余顶点}，若v与T中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
从T中选取一个距离v最小的顶点k，把k加入S中（该选定的距离就是v到k的最短路径长度）。
以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值为顶点k的距离加上边上的权。
重复步骤2和3直到所有顶点都包含在S中。

伪代码：
function Dijkstra(Graph, source):dist[source]  := 0                     // 源点到源点的距离为0for each vertex v in Graph:            // 初始化if v ≠ sourcedist[v]  := infinity           // 从源点到各个节点的距离初始化为无穷大add v to Q                         // 把所有节点都加入队列Q中while Q is not empty:                  // 主循环v := vertex in Q with min dist[v]  // 第一次循环，返回的必然是源点remove v from Q for each neighbor u of v:           // 遍历v的所有邻接节点alt := dist[v] + length(v, u)if alt < dist[u]:               // 找到了到u的更短的路径dist[u]  := alt            // 更新到u的距离 return dist[]end function

package step4;import java.util.*;public class ShortestPath {private int V;//顶点数private int E;//边数private int[] dist;private ArrayList<Integer>[] adj;//邻接表private int[][] weight;//权重public ShortestPath(int v, int e) {V = v;E = e;dist = new int[V + 1];adj = new ArrayList[V + 1];weight = new int[V + 1][V + 1];for (int i = 0; i <= this.V; i++) {adj[i] = new ArrayList<Integer>();}}public void addEdge(int u, int v, int w) {adj[u].add(v);adj[v].add(u);weight[u][v] = weight[v][u] = w;}public int[] Paths(int source) {/********** Begin *********/for (int i = 1; i <= V; i++) {//所有点的距离初始化为无限大dist[i] = Integer.MAX_VALUE;}dist[source]=0;//初始点初始化为0boolean[] st=new boolean[V+1];//判断是否以这个点为起点遍历过for(int i=0;i<V;i++)//V个顶点都要遍历一次{int t=-1;for(int j=1;j<=V;j++)//找到V个顶点中，哪个点到起点的距离最小，先以这个点更新其他点{if(!st[j]&&(t==-1||dist[t]>dist[j]))//如果没遍历过，并且比当前的小或是第一个数，则记录{t=j;//保存找到的顶点}}st[t]=true;//将这个点标记for(int j=1;j<=V;j++)//更新V个顶点的距离{if(weight[t][j]!=0)//如果权值不为0，则判断是否更新，为0代表没有连接dist[j]=Math.min(dist[j],dist[t]+weight[t][j]);//更新距离，保存小的值}}return dist;//返回得到的距离数组/********** End *********/}/*** 打印源点到所有顶点的距离，INF为无穷大** @param dist*/public void print(int[] dist) {for (int i = 1; i <= V; i++) {if (dist[i] == Integer.MAX_VALUE) {System.out.print("INF ");} else {System.out.print(dist[i] + " ");}}}}