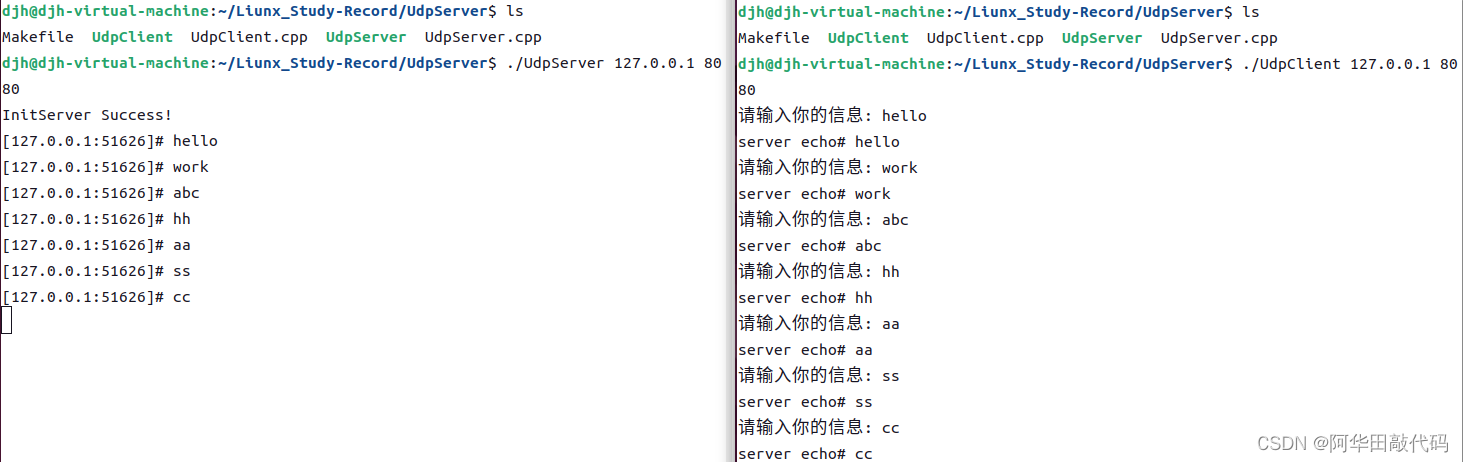
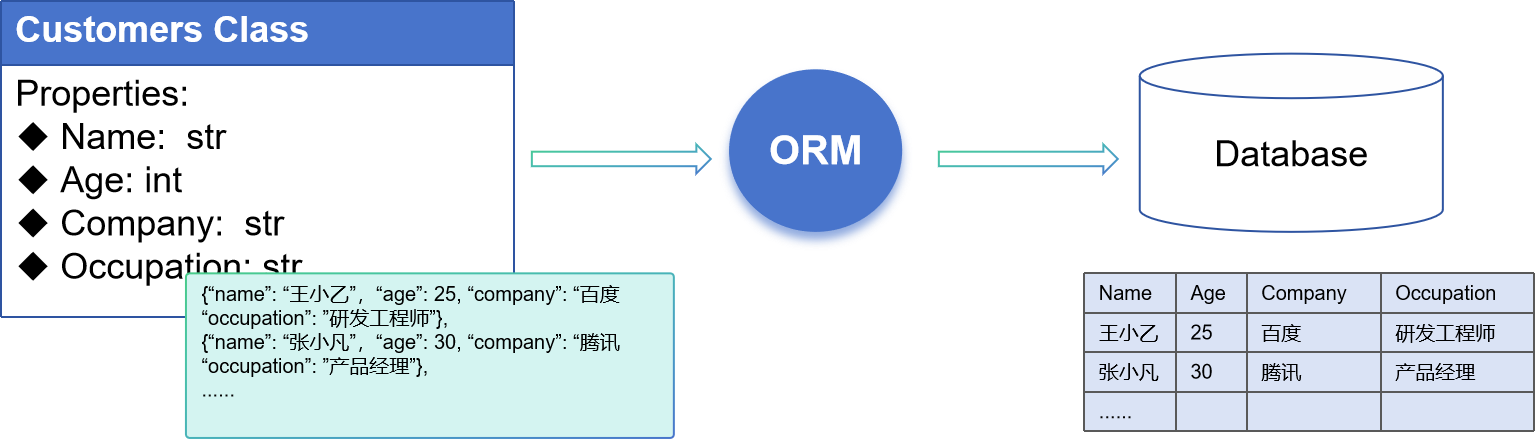
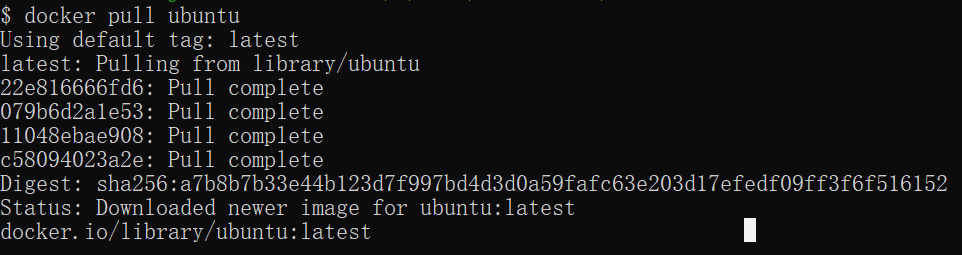
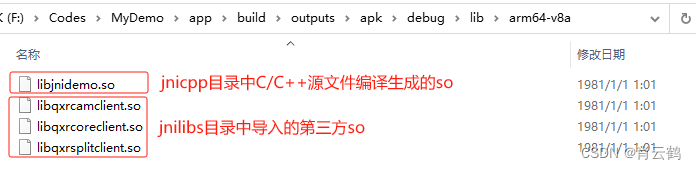
先序序列为a,b,c,d的不同二叉树的个数是()
A.13 B.14 C.15 D.16
他们有一个卡特兰数公式,就是这么解的: ,所以选B
,所以选B
上面为正确答案,下面是我个人的理解,不保证正确:
对这道题我说一下我的理解。
它这个是要确定它的不同的二叉树的个数,所以我们要先了解怎么确定自己画出来的其中一个二叉树算是一个,那么将这些二叉树统计起来就是我们要的答案。
那么怎么确定某个二叉树就算一个呢?
题目给了我们先序序列,那如果我们有中序序列,就能确定其中一个唯一的二叉树,其实先序序列和中序序列的关系就相当于一种栈的形式:
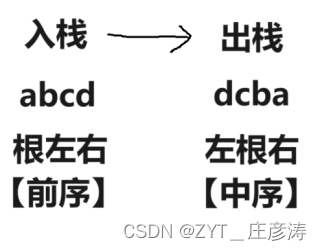
先序是【根左右】,把它理解为入栈
中序是【左根右】,把它理解为出栈
那么题目说先序序列为a,b,c,d,也就是先序abcd
那它入栈后出栈就是dcba,也就是说中序dcba
即:
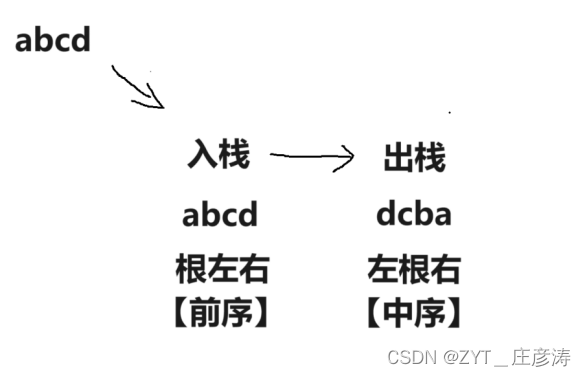
那么有了前序和中序,其实有多种画法,就我自己琢磨出来的:
要么是我自己在21年研究出的两种方法来画出其中一种:
①ZYT_先序遍历定理_前字母必比后字母平级或更高(能判断左右则不为同级)
②ZYT_中序遍历定理_前字母必在后字母左边
要么就是我24年最近研究出来的:
你可以前序画【根左///】,中序画【左根///】,这里的///代表:
比如说前序的根左右,你画完根左,后面没涉及右,其实只要不打乱根左右的顺序,把最后的右略去也是可以的。即只要不打乱规则顺序,什么根左右还是左根右,最后一个要求(如要求“右”)可以略去。
回到这幅图,
1.根据先序遍历的根左右,那么根一定是a,于是我们先画一个a,然后我们先序遍历就不用看了。

2.看中序的dcba,根据我的:②ZYT_中序遍历定理_前字母必在后字母左边,那么dcb一定在根节点a的左边,于是我们可以画:
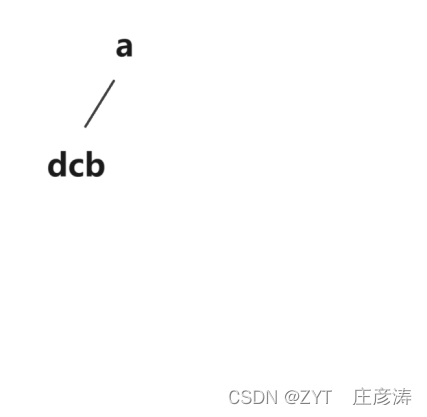
3.再根据②ZYT_中序遍历定理_前字母必在后字母左边,于是中序的dcba中,d一定在cb左边,那么画为:
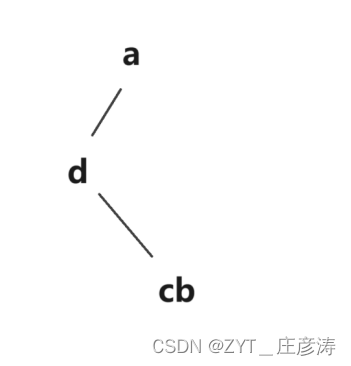
4.再根据②ZYT_中序遍历定理_前字母必在后字母左边,于是中序的dcba中,c一定在b左边,那么画为:
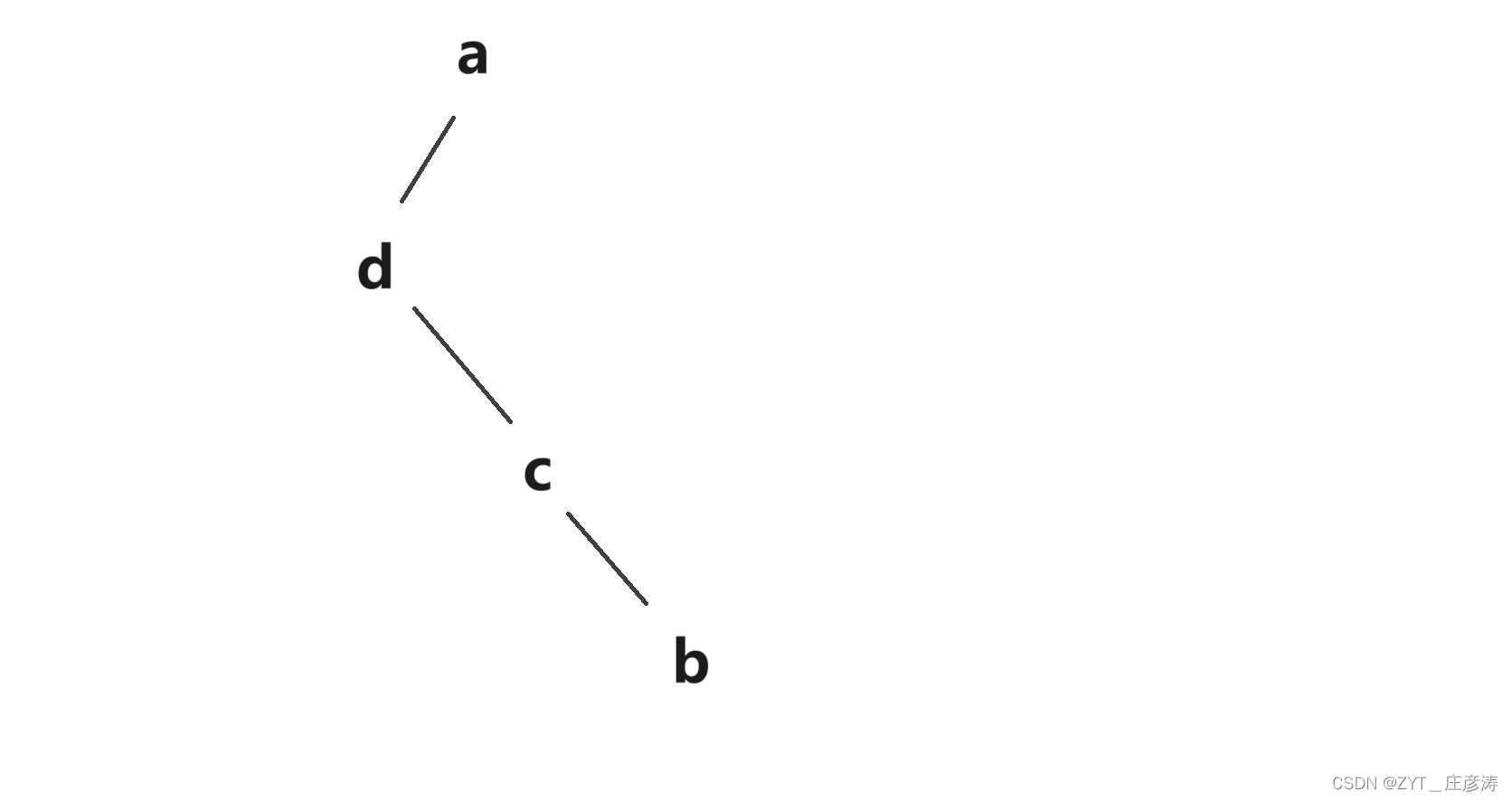
那画到这,你可能觉得不对,但上面的第2步有说过——那么dcb一定在根节点a的左边,也就是我们这里画的有偏差,调整一下就行,就是无论dcb后面拓展出来怎么画,始终保持它们这部分的队伍始终在根节点a的左边,于是调整为:
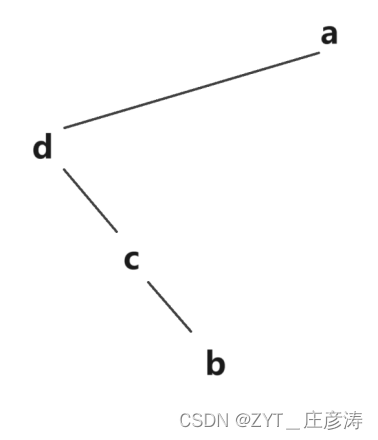
这样就是正确的其中一个二叉树啦(也就是把a移右边点,让dcb始终在根节点a的左边)
你看前序abcd【根左右】,那么a就是根节点,正确√,把bcd都理解为它左边的一部分,正确√,这里没有右,理解为把“右”忽略掉,即【根左///】,故前序的顺序我们检验正确
那么检验一下中序dcba【左根右】,这里把dcb都理解为左边的一部分,a为根,右忽略,顺序正确√。
所以这其实只是其中一种情况。我感觉这是我根据进栈和出栈的情况画出来的其中一种而已。其实我也不知正确与否,这只是我个人研究的理解,因为研究不太完善,所以好像也只能画出其中一种。
所以话说回来,答案为了方便就用了卡特兰数公式,即n为进栈的个数,这种计算就方便多了,我们进栈了abcd,那么就是n=4,那么就是:

这其中的原理我就不太知道了,有待以后补充学习。但是有个初步的眉目就是:
【就如我刚才自己画的那个,有了进栈肯定能写出出栈,那么进栈和出栈又和前序及中序相关,换句话说进栈就是前序,出栈就是中序,而有了前序及中序我就能由此推出其中的一棵二叉树,而在这个卡特兰数公式中,n为进栈的个数,也是需要我们提供进栈的信息n才能算出,这里面就有关联在里面了】。