从 GPT1 - GPT4 拆解-编程知识

从 GPT1 - GPT4 拆解

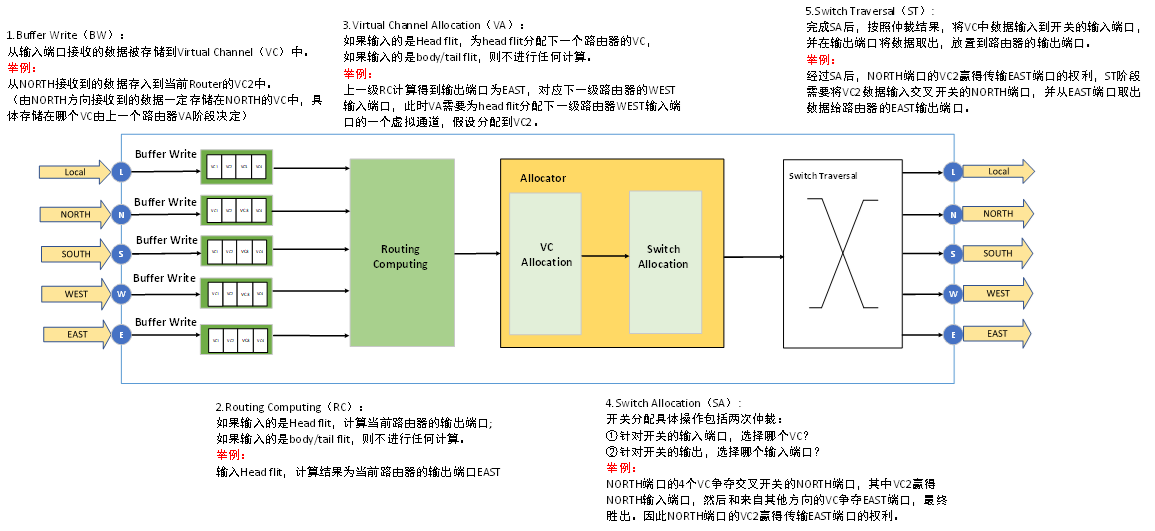
从 GPT1 - GPT4
GPT1：更适用于文本生成领域
GPT2：扩展数据集、模型参数，实现一脑多用（多个任务）
GPT3：元学习 + 大力出奇迹
InstructGPT：指示和提示学习 + 人工反馈强化学习 RLHF
GPT4

从 GPT1 - GPT4

大语言模型构建流程：

预训练阶段：使用大量数据构建基础模型，赋予模型生成文本和理解世界知识的能力
有监督微调阶段：使用高质量数据集对模型进行细化，增强其理解和执行指令的能力
奖励建模阶段：构建模型以评估文本质量，为强化学习提供基础
强化学习阶段：根据用户反馈调整模型，以生成更高质量的文本

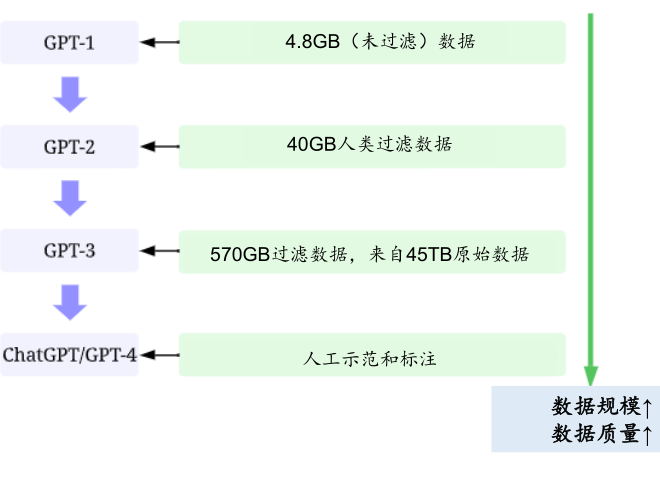
训练数据：

GPT1：更适用于文本生成领域

GPT-1：仅使用Transformer的解码器部分。

是一个自回归模型，使用了单向（从左到右）的训练方式。

它预测下一个词是基于之前所有词的。

其自回归特性，它更擅长根据之前的上下文生成文本。

主要用于文本生成任务，如文本补全、翻译、摘要等。

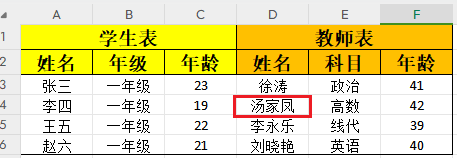
12 个（图中12x）Transformer的解码器组成：

左边：

展示了模型的主要组件，包括12层的堆叠结构
这些层包括文本和位置嵌入层（Text & Position Embed），多头遮蔽自注意力（Masked Multi Self Attention），层归一化（Layer Norm），和前馈网络（Feed Forward）。
在顶部是文本预测分类器（Text Prediction Classifier），用于输出模型预测的结果。

右边：

展示了该模型如何被应用于四种不同的NLP任务：分类（Classification）、蕴含（Entailment）、相似性（Similarity）和多项选择（Multiple Choice）。
每种任务的处理流程都有所不同，但都遵循着开始（Start）、文本（Text）/前提（Premise）/假设（Hypothesis）/答案（Answer）等部分的提取（Extract），之后通过Transformer处理，最后通过一个线性层（Linear）得到结果。
这些流程说明了模型如何处理不同类型的输入，如在相似性任务中比较两段文本，在多项选择任务中从多个选项中选择一个答案等。

无监督预训练：

给定一个无标签的序列u＝｛u1，···，un｝，优化目标是最大化下面的似然函数：

$transformer_block ( h l − 1 ) ∀ i ∈ [ 1 , n ] P ( u ) = softmax ( h n W e T ) \begin{gathered} L_{1}(\mathcal{U}) =\sum_i\log P(u_i|u_{i-k},\ldots,u_{i-1};\Theta) \\ h_0=UW_e+W_p \\ h_l=\text{transformer\_block}(h_{l-1})\forall i\in[1,n] \\ P(u)=\text{softmax}(h_nW_e^T) \end{gathered}$

这个公式描述的是一个语言模型的工作原理，一步步拆解：

首先，你有一串没有标记的词语，就像一串珍珠，我们叫它u。这串珍珠里每一颗都有它的位置，比如u1, u2, ... , un，就像是第1颗, 第2颗, ... , 最后一颗。
要猜每颗珍珠（每个词）是什么，只能看它前面几颗珍珠（前面的词）。这就是L1(U)这个公式告诉我们的，我们要尽可能地猜得准确，这样游戏得分就会越高。
游戏开始前，我们给每颗珍珠配上了一个UWe，让它们看起来更容易被识别，还有一个计分板Wp记录分数。
然后，我们开始一轮轮游戏，每一轮我们都用transformer_block来帮助我们，让我们更好地猜下一颗珍珠。这个超级电脑每轮都会变得更聪明。
最后，当我们猜完所有的珍珠后，超级电脑会使用softmax来告诉我们每颗珍珠最可能是什么。

你在玩一个猜词游戏，你要猜的不是珍珠，而是一连串的词，电脑会帮你记住前面的词，然后猜下一个词。

你想让你的得分越高越好，因为这意味着你猜的越准确。

游戏规则，就是最大化这个似然函数L1(U)，这个函数告诉我们我们的猜词游戏得分多高。

有监督的精调：

对于有标签的数据集C，每个实例有m个输入token｛x1，．．．，xm｝和标签y组成

$\begin{gathered}P(y|x^1,\ldots,x^m)\overset{.}{\operatorname*{=}}\mathrm{softmax}(h_l^mW_y)\\\\L_2(\mathcal{C})=\sum_{x,y}\log P(y|x^1,\ldots,x^m)\\\\L_3(\mathcal{C})=L_2(\mathcal{C})+\lambda L_1(\mathcal{C})\end{gathered}$

就像教一台机器分辨不同的水果一样。

在这个任务中，每个水果（比如苹果、香蕉、橘子）都有一些特征（比如形状、颜色、大小），这些特征就像是输入的tokens（令牌）。

第一部分（P(y|x^1,…,xm)）：预测标签的概率
- 这个部分的公式是在计算机器根据水果的特征来预测这个水果是什么的概率。
- 比如，给定一个水果的形状、颜色和大小，机器会计算出这个水果是苹果、香蕉还是橘子的概率。
- "softmax"是一种特殊的数学函数，它可以把输入的数据转换成概率，使得所有可能的水果的概率加起来总和是1。
第二部分（L_2©）：损失函数
- 这部分是一个“损失函数”，它用来衡量机器的预测有多准确。
- 如果机器的预测很准确，这个损失值会很小；如果预测不准确，损失值就会变大。
- 具体来说，这个损失函数是计算机器预测的概率和实际的标签（比如，这个水果真的是苹果还是香蕉）之间的差异。
第三部分（L_3©）：正则化的损失函数
- 最后这部分是在原来的损失函数基础上加了一点调整，这种调整叫做“正则化”，它有助于让机器学习得更好。
- 如果不使用正则化，这个模型可能会非常“刻板”。它可能只学会识别它看到的那些特定的苹果和橘子，而不是学会识别这两种水果的一般特征。
- 这里的λ是一个小数，用来控制正则化的程度。

GPT1 训练数据：BookCorpus 7000 本书籍。

核心思想是：

做打生成式，输入都是一问一答
使用无监督生成式预训练代替传统标注数据，这意味着它在训练时不依赖于标记好的数据集。

让机器通过广泛阅读来自主学习语言，通过阅读大量文本来学习如何生成文本，而不是依赖于特定的“问题-答案”对。

这种方法允许GPT-1掌握语言的广泛用法，并能在各种情境中灵活应用所学知识，而不仅仅是回应特定的提示或问题。

GPT2：扩展数据集、模型参数，实现一脑多用（多个任务）

GPT1 的问题在于：

一个简单的专家模型，还不是很专家
只能做一个特定任务，不能迁移

GPT2 扩展数据集、模型参数，实现一脑多用（多个任务）。

$\begin{aligned}p(x)&=\prod_{i=1}^np(s_n|s_1,\ldots,s_{n-1})&&p(\text{output|input})\\\\p(s_{n-k},\ldots,s_n|s_1,s_2,\ldots,s_{n-k-1})&&p(\text{output|input,task})\end{aligned}$

GPT2被训练来学习很多很多的故事和对话：

第一部分（p(x)）：预测下一个词
- 这部分的公式是关于如何预测故事中的下一个词。
- 比如，如果到目前为止的故事是“有一个小猫爬上了…”，机器人需要猜测下一个词是什么。
- 它通过学习大量的故事来做出这样的猜测，可能会猜“树”因为在它读过的很多故事里，小猫常常爬上树。
- 公式中的 “s_1, …, s_{n-1}” 就像是到目前为止的故事部分，而机器人要预测的就是“s_n”，也就是接下来的词。
第二部分（p(output|input)）：基于输入预测输出
- 这部分是说，如果我们给机器人一些特定的信息或提示（input），它可以根据这些信息来讲故事（output）。
- 比如，如果我们告诉机器人“讲一个关于太空的故事”，它就会基于它学过的关于太空的知识来讲故事。
第三部分（p(output|input, task)）：针对特定任务的预测
- 最后这部分是更具体的。这里不仅仅是告诉机器人要讲什么样的故事（input），还告诉它要完成一个特定的任务（task）。
- 比如，“讲一个关于太空的故事，故事里要有一只名叫Tom的宇航员猫”。
- 这时，机器人会根据这些更详细的要求来讲一个符合要求的故事。

牛逼之处，在于当模型容量非常大、数据量非常丰富的时候，仅仅靠训练语言模型的学习便可以完成其他有监督学习的任务。

通过阅读海量的文本，学到了很多东西。

GPT-2这样的模型因为读过很多东西，学了很多知识，所以它能处理各种不同的任务，就算这些任务以前没直接学过。

GPT2 训练数据：Reddit 高赞文章 800 万篇 40G。

GPT3：元学习 + 大力出奇迹

GPT2 的极限没有被开发出来，模型参数、训练数据还是太少了。

GPT3 参数增长到 1750 亿，45 TB 训练数据。

除了大，GPT3 还提出了提示的情景式学习方式。

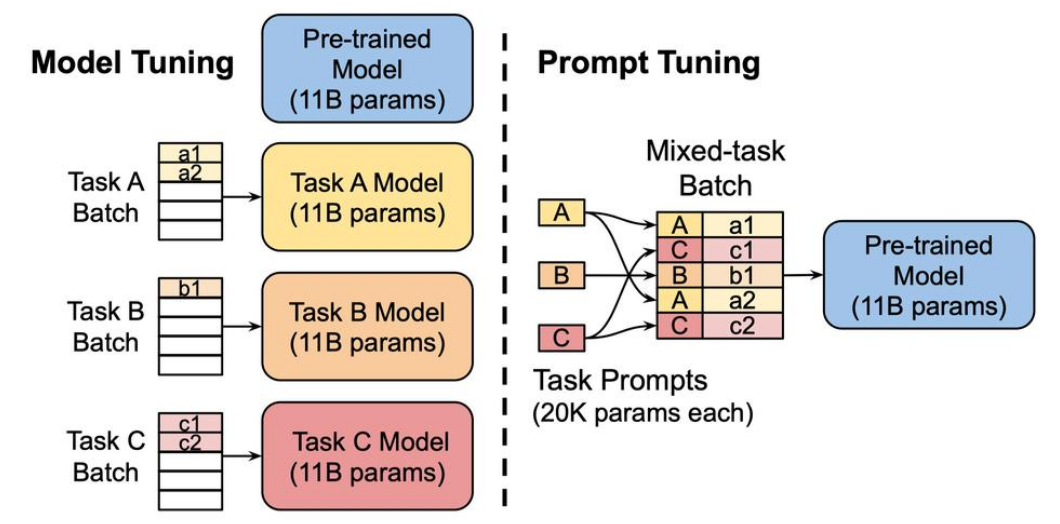
左图是传统的方式，右图是GPT3提出的提示引导。

在一个预训练模型处理多种不同的任务中，不是每个任务都有一个单独的模型，而是使用“提示”（Prompts）来指导同一个预训练模型完成不同的任务。

这种方法的优势在于它不需要针对每个任务训练一个完整的模型，只需要调整相对较小的提示部分，就可以引导同一个大模型完成不同的任务。

这种原理来自于 — 元学习。

通过学习任务间共性和差异，发现规律，并迁移到新任务上。

使用少量数据，寻找初始化范围，使得模型在有限数据集上，快速拟合。

prompt学习方法，根据提示情景，有针对的回答。

用户：你觉得tiktok是个好应用吗？GPT：Do you think tiktok is a good app?
GPT：tiktok 是什么呀？
GPT：我不能做出有偏袒的评价。

提示学习方法的核心在于，通过给模型不同的指令或情境，可以影响模型的输出，使其更适合特定的用途或遵循特定的交流原则。

在实际应用中，这使得同一个模型可以在不同的情境下以不同的方式回答相同的问题，这非常有用，尤其是在需要模型适应多种对话风格和需求的场合。

有 3 种学习方式：

零样本：没有任何例子，直接干活
单样本：给一个例子，直接干活
少量样本：给几个例子，直接干活

GPT3 只需要给一个或者几个例子，就能一直按照原意去干活。

GPT3 受限 Transformer 建模能力，对于长文章会重复输出；也不能保证生成的内容不包含敏感内容。

InstructGPT：指示和提示学习 + 人工反馈强化学习 RLHF

GPT-3.5 是 GPT-3 的一个更新版本，提供了更好的性能和更准确的语言理解能力。

InstructGPT 在 GPT-3.5 的基础上通过进一步的训练来专门优化执行指令的能力。

InstructGPT 是 GPT-3.5 的一个特定版本，专门针对理解和执行复杂指令进行了优化，旨在提供更加精准的指令执行和更好的用户体验。

这意味着 InstructGPT 更擅长根据用户给出的指令产生相关的输出，比如回答问题、解释概念、生成文本等。

指示学习和提示学习：

指示学习：更加依赖于人类提供的示范数据和指令 — 快速获取专业知识和技能
提示学习：更加依赖于模型自身的推断能力，以及少量的提示信息 — 缩小搜索空间，更准确学习任务的关键特征和规律

俩者，是一起用的。

人工反馈强化学习 RLHF。

单纯训练得到的模型并不可控，模型是训练集分布的拟合，当生成数据时，训练数据的分布极大影响生成内容的质量
不能只靠训练数据的影响，要人为可控的保证生成数据的真实性、可用性、无害性
就要引入人类偏好的机制，使用强化学习引入
强化学习是通过奖励函数来指导模型训练

训练流程：

数据集
有监督微调 SFT：问答对
奖励模型 RM：模型生成的，人工排序打分
强化学习 PPO：无人工标注答案，问题来自用户

RM 损失函数：

$\operatorname{loss}\left(\theta\right)=-\frac{1}{\binom{K}{2}}E_{(x,y_w,y_l)\sim D}\left[\log\left(\sigma\left(r_\theta\left(x,y_w\right)-r_\theta\left(x,y_l\right)\right)\right)\right]$

目标是，最大化人类喜欢（好回答）、不喜欢的（坏回答）的差值。

$r_\theta(x, y_w)$ 和 $r_\theta(x, y_l)$ :
- $r_\theta$ 代表模型，其任务是给每个回答打分。
- $x$ 表示问题， $y_w$ 表示好回答，而 $y_l$ 表示坏回答。
- $r_\theta(x, y_w)$ 是模型给好回答的分数，而 $r_\theta(x, y_l)$ 是模型给坏回答的分数。
$\sigma$ :
- 这个符号表示sigmoid函数，一种特殊的数学函数。
- 它将任何数值转换为0到1之间的数，这有助于将分数转换为概率（类似于百分比）。
相减和对数:
- 我们计算好回答的分数减去坏回答的分数，然后使用 $s i g m o i d$ 函数将这个差值转换为概率。
- 接着，我们取这个概率的对数。对数是一种数学运算，它在处理概率时更加方便。
期望值 $E$ 和平均:
- 公式中的 $E$ 表示期望值，即对许多不同的问题和回答重复此过程，然后计算平均结果。
- 通过平均这些结果，我们确保模型在各种情况下都能学习区分好回答和坏回答。
负号和最小化损失:
- 公式前的负号表示我们希望最小化这个值。
- 在机器学习中，我们通常尝试最小化称为“损失”的值，这告诉我们模型的表现有多差。
- 通过最小化这个损失，我们实际上在教模型更好地区分好回答和坏回答。

强化学习 PPO：

$\begin{aligned} objective (\phi)=& E_{(x,y)\sim D_{\pi_{\phi}^{\mathrm{RL}}}}\left[r_{\theta}(x,y)-\beta\log\left(\pi_{\phi}^{\mathrm{RL}}(y\mid x)/\pi^{\mathrm{SFT}}(y\mid x)\right)\right]+ \\ &\gamma E_{x\sim D_{\mathrm{pretrain}}}\left[\operatorname{log}(\pi_{\phi}^{\mathrm{RL}}(x))\right] \end{aligned}$

目标函数 $(\phi)$ :
- 这个公式是一个目标函数，用于指导机器学习模型的学习过程。
- $\phi$ 代表模型的参数，即模型在学习过程中需要调整的部分。
第一部分:
- $E_{(x,y)\sim D_{\pi_{\phi}^{\mathrm{RL}}}}\left[r_{\theta}(x,y) - \beta\log\left(\pi_{\phi}^{\mathrm{RL}}(y\mid x)/\pi^{\mathrm{SFT}}(y\mid x)\right)\right]$ 这部分可能看起来复杂，但我们可以分步骤来理解：
  - $E$ 代表期望值，即我们在许多不同的实例（ $x, y$ ）上计算此公式然后取平均。
  - $r_{\theta}(x,y)$ 是评估回答 $y$ 质量的分数， $x$ 是问题。
  - $\beta$ 是一个调节因子，用于平衡公式的两个部分。
  - $\log\left(\pi_{\phi}^{\mathrm{RL}}(y\mid x)/\pi^{\mathrm{SFT}}(y\mid x)\right)$ 是两个不同模型对同一问题的回答概率的比率，帮助模型学习在不同情况下做出更好的选择。
第二部分:
- $\gamma E_{x\sim D_{\mathrm{pretrain}}}\left[\log(\pi_{\phi}^{\mathrm{RL}}(x))\right]$ 这部分帮助模型记住在预训练阶段学到的知识。
- $\gamma$ 是另一个调节因子，用于控制这部分对整体目标的影响。
- $E_{x\sim D_{\mathrm{pretrain}}}$ 表示我们在预训练数据上计算这部分的平均值。
- $\log(\pi_{\phi}^{\mathrm{RL}}(x))$ 是模型对给定输入 $x$ 的反应概率的对数。