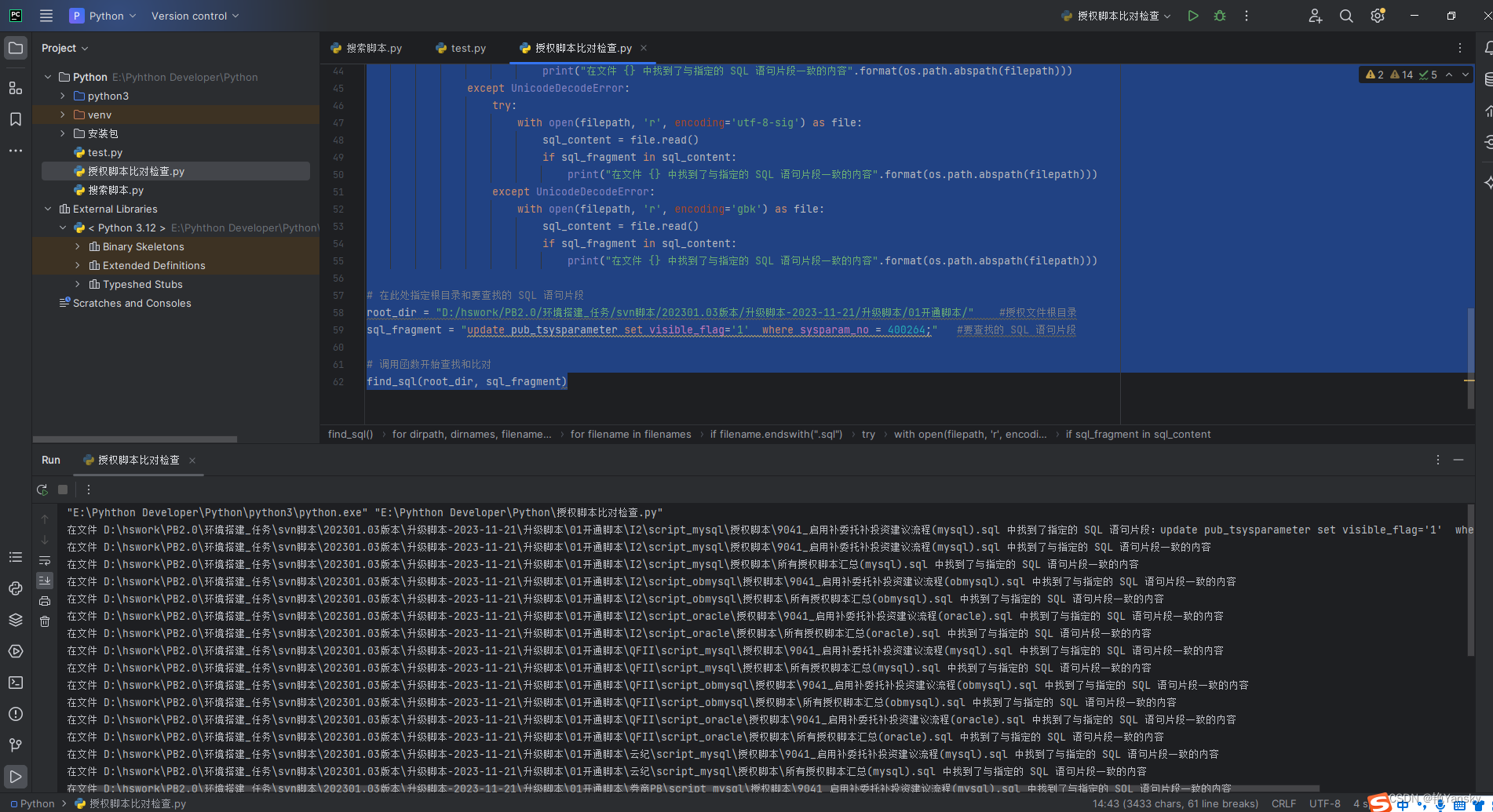
寒假刷题
92. 递归实现指数型枚举
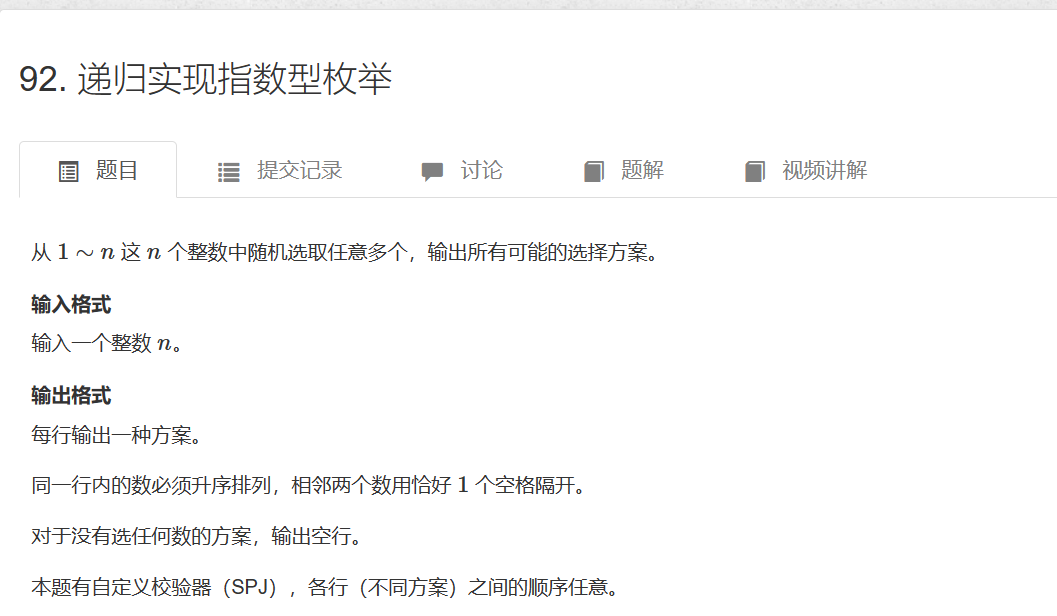
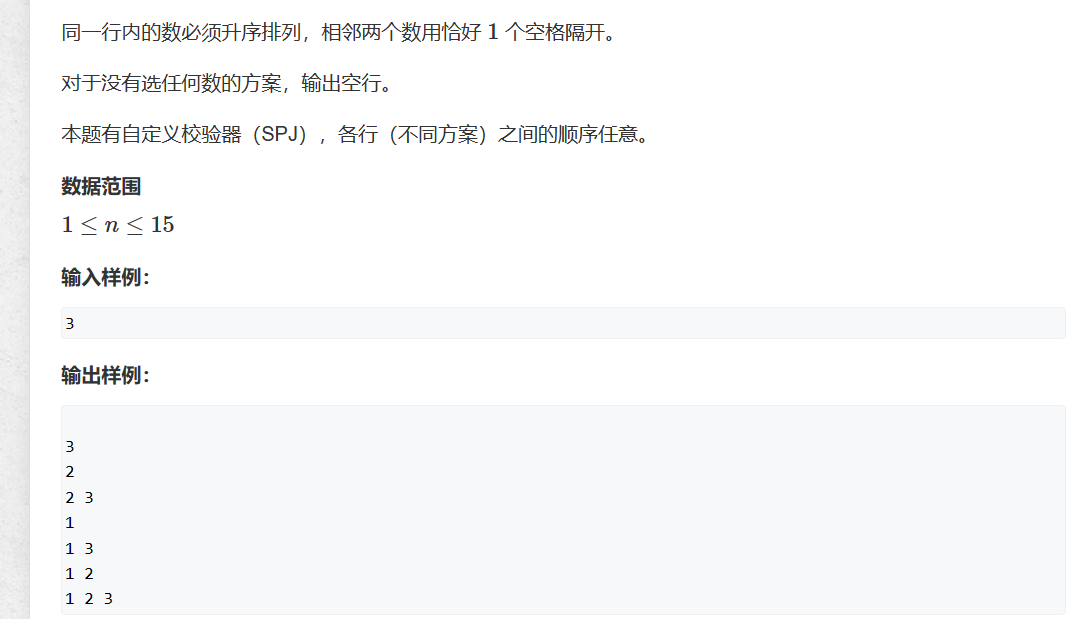
解法1递归
使用递归对每一个坑位进行选择,每个坑位有两种选择,填或者不填,使用st数组来记录每个坑位的状态,u来记录已经有多少坑位有了选择。

每个坑位有2钟选择,n个坑位的复杂度就是2的n次方。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 16;
int n;
int st[N];
void dfs(int u){if(u>n){for(int i = 1;i<=n;i++){if(st[i]==1)printf("%d ",i);}printf("\n");return;}st[u] = 1;dfs(u+1);st[u]=0;dfs(u+1);
}
int main(){scanf("%d",&n);dfs(1);return 0;
}
坑位的下标和这个坑位的数字是存在对应关系的,所以可以用一个u来控制递归的出口。我们只关心u位置是否有数字。
st[u] = 1;
dfs(u+1);
这两句相当于是将这个位置画对勾,然后跳到下一个位置进行选择
st[u]=0;
dfs(u+1);
这两句就是这个位置不填数进入下一轮,顺便回到dfs之前的状态。(这题无所谓)
解法2二进制压缩
1-n的所有整数排列的方案可以看作一个二进制序列,例如1-3的排列中,1 3就对应二进制101。有数字用1表示,没有数字用0表示。
1-n共有2的n次方钟方案。将所有方案数枚举,然后判断位数是否是1。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int main()
{scanf("%d",&n);for(int i = 0;i < 1<<n;i ++){for(int j = 0;j < n;j ++){if(i >> j & 1)printf("%d ",j + 1);}printf("\n");}return 0;
}
94. 递归实现排列型枚举
这题就是一个全排列问题,和上一题的区别是很明显的。上一个的每个坑位的数字是固定的,可能有或没有,这个题的每个坑位的数是不固定的,且必须有。这个题需要使用st记录是否使用过。这个st和上一个题的st代表的意义不一样。
使用循环来进行dfs。循环从1开始,到n结束。通过st[i]可以知道数字i是否被使用过。如果没被使用过就使用i,然后进入下一层搜索。使用后一定要恢复现场。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10;
int m,st[N],ans[N];
int n;
void dfs(int x)
{if(x > n) {for(int i = 1;i <= n;i ++){printf("%d ",ans[i]);}printf("\n");}for(int i = 1;i <=n;i ++){if(!st[i]){st[i] = 1;ans[x] = i;dfs(x+1);st[i] = 0;}}
}
int main()
{scanf("%d",&n);dfs(1);return 0;
}
717. 简单斐波那契
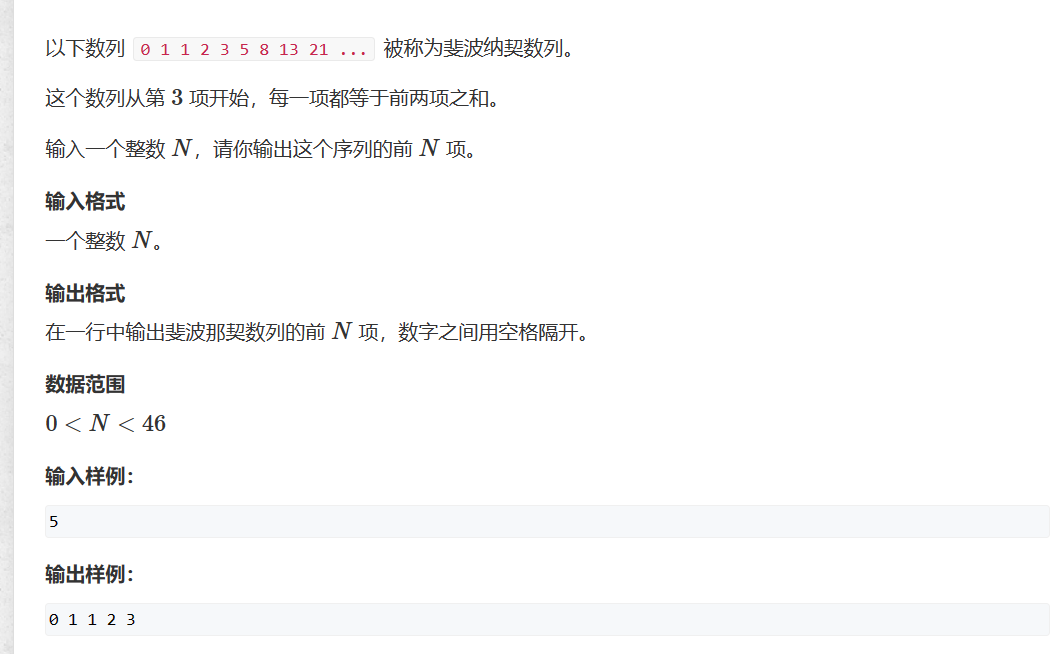
使用递推来进行求解,通过观察可以发现这个数列的第n项只与n-1和n-2项有直接关系,所以使用三个变量a b fn,依次向后轮转。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){int n,fn;scanf("%d",&n);int a = 0,b = 1;for(int i = 1;i <= n;i ++){cout<<a<<" ";fn = a+b;a=b,b=fn;}
}
95. 费解的开关

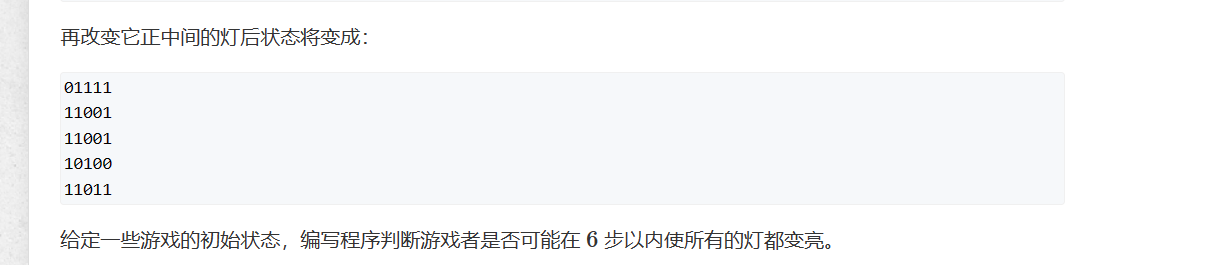

样例

改变右上角的开关


两步即可让所有的灯变亮。
观察题意可以发现能影响灯本身的除了灯自己还有灯上下左右的灯,可以枚举第一行灯的32种按法,记得备份原数组,然后从第一行按到第四行,第i行可以通过第i+1行的灯来控制,遍历完第四行后,看看第五行还有没有灭的灯,如果有的话,那这个方案就是不可行的。因为没有第六行来控制第五行。如果第五行全亮,那这个就是可以调,判断一下和ans哪个更小。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6;
char g[N][N],backup[N][N];
int n;
int dx[] = {1,-1,0,0,0};
int dy[] = {0,0,-1,1,0};
void turn(int x,int y){for(int i = 0;i < 5;i ++){int a = x + dx[i];int b = y + dy[i];if(a < 0 || b < 0 || a > 4 || b > 4)continue;g[a][b] ^= 1;}
}
int main(){scanf("%d",&n);while(n --){for(int i = 0;i < 5;i ++)scanf("%s",g[i]);int ans = 10;for(int op = 0;op < 32;op ++){memcpy(backup,g,sizeof g);int step = 0;for(int i = 0;i < 5;i ++){if(op >> i & 1){turn(0,i);step ++;}}for(int i = 0;i < 4;i ++){for(int j = 0;j < 5;j ++){if(g[i][j] == '0'){turn(i+1,j);step ++;}}}int drak = 0;for(int j = 0;j < 5;j ++){if(g[4][j] == '0'){drak = 1;break;}}if(drak == 0)ans = min(ans,step);memcpy(g,backup,sizeof g);}if(ans > 6)ans = -1;cout << ans <<endl;}return 0;
}
93. 递归实现组合型枚举


这题与全排列的区别就是字典序,只需要在判断是否使用过的时候加上一个判断,条件是当前的i是否大于ans数组的的最后一个元素,大于往里面添加,小于直接就跳过即可。ans数组初始化时要将元素变为-1,否则开头将无法添加。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 26;
int n,m;
int ans[N] = {-1},st[N]={0};
void dfs(int c,int m){if(c > m){for(int i = 1;i <= m; i ++){cout << ans[i] << " ";}cout<<endl;return;}for(int i = c ;i <= n; i ++){if(!st[i]&&i > ans[c-1]){ans[c] = i;st[i] = 1;dfs(c + 1,m);st[i] = 0;}}
}
int main(){scanf("%d%d",&n,&m);dfs(1,m);return 0;
}
1209. 带分数

题意是
n = a + b / c n = a + b/c n=a+b/c
等式两边同时×c
c ∗ n = c ∗ a + b c*n = c*a+b c∗n=c∗a+b
通过dfs枚举a和c,然后计算出b,然后遍历st数组看看是否b的每一位都没有被用到。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 30;
int st[N],backup[N];
int n,ans,test;
bool check(int a,int c)
{long long b = (long long) n * c -a * c;if(!a || !b || !c)return false;memcpy(backup,st,sizeof st);while(b){int ge = b % 10;if(ge == 0 || backup[ge])return false;backup[ge] = 1;b /= 10;}for(int i = 1;i <= 9;i ++){if(backup[i] == 0) return false;}return true;
}
void dfs_c(int a,int c)
{if(check(a,c))ans ++;for(int i = 1; i <= 9; i ++){if(st[i] == 0){st[i] = 1;dfs_c(a,c*10 + i);st[i] = 0;}}
}
void dfs_a(int a)
{if(a > n)return;if(a)dfs_c(a,0);for(int i = 1;i <= 9; i ++){if(st[i] == 0){st[i] = 1;dfs_a(a*10 + i);st[i] = 0;}}
}
int main()
{scanf("%d",&n);dfs_a(0);cout << ans << endl;return 0;
}
116. 飞行员兄弟
和费解的开关类似,只不过这个题的数量比较下,所以枚举所有行的全部可能,共65536种,对每一种方案进行操作,记录最少的方案数。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define x first
#define y second
using namespace std;typedef pair<int,int> PII;
const int N = 5;
char st[N][N],backup[N][N];
vector <PII> ans;
int get(int x,int y)
{return x*4 + y;
}
void turn(int x,int y)
{if(st[x][y]=='+')st[x][y]='-';else st[x][y]='+';
}
void turnall(int x,int y)
{for(int i = 0;i < 4;i ++){turn(x,i);turn(i,y);}turn(x,y);
}
int main()
{for(int i = 0;i < 4;i ++){scanf("%s",st[i]);}for(int i = 0;i < 1 << 16;i ++){vector <PII> step;memcpy(backup,st,sizeof st);for(int x = 0;x < 4;x ++){for(int y = 0;y < 4;y ++){if(i >> get(x,y) & 1){turnall(x,y);step.push_back({x,y});}}}int dark = 0;for(int x = 0;x < 4;x ++){for(int y = 0;y < 4;y ++){if(st[x][y]=='+'){dark = 1;break;}}}if(dark == 0){if(ans.empty()||ans.size() > step.size()) ans = step;}memcpy(st,backup,sizeof st);}cout << ans.size() << endl;for(auto p:ans){cout << p.x+1<<" "<<p.y+1<<endl;}return 0;
}
1208. 翻硬币
有个初始态有个结束态。将初始态与结束态一一对比,遇到不一样的就将移动次数加一并且变换硬币状态。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int ans;
string start,aim;
void turn(int i)
{if(start[i]=='*')start[i] = 'o';else start[i] = '*';
}
int main()
{cin>>start>>aim;for(int i = 0;i < start.size() - 1;i ++){if(start[i]!=aim[i])turn(i+1),ans++;}cout << ans <<endl;return 0;
}