AtCoder ABC 336（A~F）

A - Long Loong

        模拟

// Problem: A - Long Loong
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_a
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve() 
{cin >> n;string s = "";s += 'L';for(int i = 0 ; i < n ; i ++){s += 'o';}s += "ng";cout << s;
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
//	cin>>t;while(t--){solve();}return 0;
}

B - CTZ

        还是模拟

// Problem: B - CTZ
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_b
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve() 
{int ans = 0;cin >> n;while(n){if(n & 1)break;elseans++;n/=2;}	cout << ans;
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;//cin>>t;while(t--){solve();}return 0;
}

C - Even Digits

        找出由0 , 2 , 4 , 6 , 8 组成的第x大数，模拟（注意一开始不能取0 ， 因此其实是一个开头为4，其余都是5的进制数）。

// Problem: C - Even Digits
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
int mask[5] = {0 , 2 , 4 , 6 , 8};
void solve() 
{LL n;cin >> n;n--;LL k = 1;while(k * 5 <= n){k *= 5;}while(k > 0){int t = n / k;cout << mask[t];n -= t * k;k /= 5;}
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;//cin>>t;while(t--){solve();}return 0;
}

D - Pyramid

        定义1, 2, 3...k-1, k, k-1...3,2,1为长度为k的好序列，现给定一组数组，你可以选中其子序列，同时将其中的数减去若干，组成一组好序列。求好序列的最大长度。

        二分求长度，从头开始遍历，然后判断能否形成这个好序列，首先从头到尾尽可能的组成一组好序列，若到某个数时无法和前面的数组成好序列，那就将这个数变成新序列的第a_{i}位，其中a_{i}为这个数的值，这样做必然是最优的。

        

// Problem: D - Pyramid
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve() 
{int n;cin >> n;for(int i = 0 ; i < n ; i ++){cin >> a[i];}	int l = 1 , r = (n + 1) / 2;auto check = [&] (int len){int cnt = 0;for(int i = 0 ; i < n ; i ++){if(cnt < len){if(a[i] >= cnt + 1){cnt++;}else{cnt = a[i];}}else{if(a[i] >= len - (cnt - len + 1)){cnt++;}else{cnt = a[i];}}if(cnt >= len * 2 - 1){return true;}}return false;};while(l < r){int mid = (l + r + 1) / 2;if(check(mid)){l = mid;}else{r = mid - 1;}}cout << l << endl;
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
//	cin>>t;while(t--){solve();}return 0;
}

E - Digit Sum Divisible

        题意：从1~N，输出其中各个位数之和能够整除其的数量。

        思路：数位DP，首先可以发现N\leq 1e14，因此位数之和应当小于9 * 14。所以我们可以钦定位数和，然后求出每个位数和分别有多少个数满足条件。

        定义dp[i][sum][res][st]代表了数的前i位，各个位数之和为sum，余数为res的和。其中st表示是否为上界（其中0代表未达到上界，1代表还处于上界之中）。每一轮都是将新的数插入之前数的最后，假设加的数为num，那么新的余数res就变成了res * 10 + num 模上位数和。最终答案加上第N的位数位，总和为钦定的位数和，余数为0，状态为0或者1的总数。

// Problem: E - Digit Sum Divisible
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_e
// Memory Limit: 1024 MB
// Time Limit: 10000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
#define int long long 
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int dp[20][200][200][2];//第i位,和为x,余数为y的个数,是否为上界的情况
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve() 
{string n;cin >> n;int len = n.size();LL ans = 0;for(int i = 1 ; i <= 9 * 14 ; i ++){//钦定位数和memset(dp , 0 , sizeof dp);dp[0][0][0][1] = 1;for(int j = 1 ; j <= len ; j ++){//14for(int k = 0 ; k <= 9 * 14 ; k ++){//总和100for(int num = 0 ; num <= 9 ; num ++){if(k + num > i){continue;}for(int st = 0 ; st < 2 ; st ++){if(st && num > (n[j - 1] - '0')){continue;}for(int res = 0 ; res < i ; res ++){int now_res = (res * 10 + num) % i;dp[j][k + num][now_res][(st && (num == n[j - 1] - '0'))] += dp[j - 1][k][res][st];}}}}	}ans += dp[len][i][0][0] + dp[len][i][0][1];}cout <<ans;
}            
signed main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
//	cin>>t;while(t--){solve();}return 0;
}

F - Rotation Puzzle

        题意：给定一个长为h,宽为w的二维数组，其中每次操作能够将长为h-1,宽为w - 1的块翻转180°。求最终能否变成一个1,2,3,4,5....的顺序数组。限定操作最多为20次。

参考图片

        

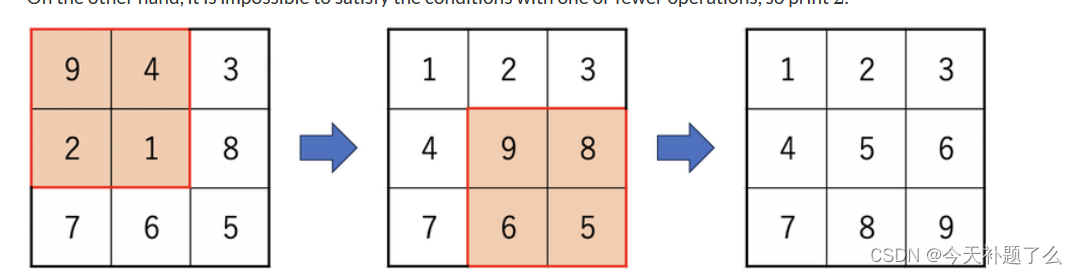
        思路：（折半搜索）首先肯定考虑DFS遍历所有情况，然后每一轮的情况共有4种，那么总共的复杂度为O(4^{20})肯定是超的。因此考虑从头开始dfs和从尾开始dfs，这样两次dfs的时间复杂度均为 O(4^{10})，然后若有重复的，那么就代表能够从头走到尾，记录一下答案即可。单纯考察折半搜索，就是写起来比较复杂

// Problem: F - Rotation Puzzle
// Contest: AtCoder - AtCoder Beginner Contest 336
// URL: https://atcoder.jp/contests/abc336/tasks/abc336_f
// Memory Limit: 1024 MB
// Time Limit: 5000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
int ans = 25;
map< vector<vector<int>> , int > mp;	
vector<vector<int>>s(9 , vector<int>(9 , 0));
void change(int l_min , int l_max ,int r_min , int r_max){for(int i = 0 ; i <= (r_max - r_min) ; i ++){int st = r_min + i;int en = r_max - i;if(st > en)break;else if(st == en){for(int j = 0 ; j <= (l_max - l_min) ; j ++){int ss = l_min + j;int ee = l_max - j;if(ss > ee)break;swap(s[st][ss] , s[en][ee]);}			}else{for(int j = 0 ; j <= (l_max - l_min) ; j ++){int ss = l_min + j;int ee = l_max - j;swap(s[st][ss] , s[en][ee]);}}}
}
void dfs(int step){if(step > 10)return;if(!mp.count(s)){mp[s] = step;}else{mp[s] = min(mp[s] , step);}change(0 , n - 2 , 0 , m - 2);dfs(step + 1);change(0 , n - 2 , 0 , m - 2);change(1 , n - 1 , 0 , m - 2);dfs(step + 1);change(1 , n - 1 , 0 , m - 2);change(0 , n - 2 , 1 , m - 1);dfs(step + 1);change(0 , n - 2 , 1 , m - 1);change(1 , n - 1 , 1 , m - 1);dfs(step + 1);change(1 , n - 1 , 1 , m - 1);	
}
void dfs2(int step){if(step > 10)return;if(mp.count(s)){ans = min(ans , step + mp[s]);}change(0 , n - 2 , 0 , m - 2);dfs2(step + 1);change(0 , n - 2 , 0 , m - 2);change(1 , n - 1 , 0 , m - 2);dfs2(step + 1);change(1 , n - 1 , 0 , m - 2);change(0 , n - 2 , 1 , m - 1);dfs2(step + 1);change(0 , n - 2 , 1 , m - 1);	change(1 , n - 1 , 1 , m - 1);dfs2(step + 1);change(1 , n - 1 , 1 , m - 1);	
}
void solve() 
{cin >> m >> n;int id = 1;for(int i = 0 ; i < m ; i ++){for(int j = 0 ; j <n ; j ++){cin >> s[i][j];}}dfs(0);id = 1;for(int i = 0 ; i < m ; i ++){for(int j = 0 ; j < n ; j ++){s[i][j] = id++;}}dfs2(0);if(ans == 25)cout << -1;elsecout << ans;
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;//cin>>t;while(t--){solve();}return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/414965.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

安全加速SCDN是什么

安全加速SCDN是什么

安全加速SCDN&#xff08;Secure Content Delivery Network&#xff0c;SCDN&#xff09; 是集分布式DDoS防护、CC防护、WAF防护、BOT行为分析为一体的安全加速解决方案。已使用内容分发网络&#xff08;CDN&#xff09;或全站加速网络&#xff08;ECDN&#xff09;的用户&…
阅读更多...
大数据工作岗位需求分析

大数据工作岗位需求分析

前言&#xff1a;随着大数据需求的增多&#xff0c;许多中小公司和团队也新增或扩展了大数据工作岗位&#xff1b;但是却对大数据要做什么和能做什么&#xff0c;没有深入的认识&#xff1b;往往是招了大数据岗位&#xff0c;搭建起基础能力后&#xff0c;就一直处于重复开发和…
阅读更多...
HTTPS：如何确保您的网站数据传输安全？

HTTPS：如何确保您的网站数据传输安全？

目录 博客前言 一.HTTPS 1.1 HTTPS简介 1.2 HTTP和HTTPS区别 1.3 TLS/SSL协议工作原理 1.3.1 TLS/SSL协议结构 1.3.2 SSL/TLS握手协议建立连接过程 1.2.3 SSL/TLS报文分析 博客前言 以下是一个关于HTTPS协议的博客前言示例&#xff1a; 欢迎来到我的博客&#xff0c;今…
阅读更多...
MySQL窗口函数（MySQL Window Functions）

MySQL窗口函数（MySQL Window Functions）

1、窗口函数基本概念 官网地址&#xff1a;https://dev.mysql.com/doc/refman/8.0/en/window-functions.html 窗口可以理解为 记录集合&#xff0c;窗口函数就是在满足某种条件的记录集合上执行的特殊函数。 即&#xff1a;每条记录都要在此窗口内执行函数。 静态窗口&#x…
阅读更多...
ITK + ANT，无法显示三维

ITK + ANT，无法显示三维

背景&#xff1a;之前用ANT保存ima格式的数据&#xff0c;选择的是保存所有的序列 用python将dicom转为nii的格式&#xff0c; import nibabel as nib import torch"""不管是nii还是nii.gz都是二维的&#xff0c;为啥呢"""fobj nib.load("…
阅读更多...
MeterSphere本地化部署实践

MeterSphere本地化部署实践

项目结构 搭建本地环境 安装JDK11&#xff0c;配置好JDK环境&#xff0c;系统同时支持JDK8和JDK11安装IEAD&#xff0c;配置JDK环境配置maven环境,IDEA配置(解压可以直接使用)无限重置IDEA试用期配置redis环境(解压可以直接使用) 配置kafka环境 安装mysql-5.7环境&#xff…
阅读更多...
恒创科技：云存储和网盘怎么区分出来？

恒创科技：云存储和网盘怎么区分出来？

随着互联网的发展&#xff0c;数据存储已成为人们日常生活中不可或缺的一部分。云存储和网盘是经常被人们提及的两种存储方式&#xff0c;均通过网络进行数据存储和访问的服务。但&#xff0c;它们在技术实现、数据安全性、访问方式和数据容量等方面存在一定的差异。要区分&…
阅读更多...
【全】OpenSSL创建生成CA证书、服务器、客户端证书及密钥说明

【全】OpenSSL创建生成CA证书、服务器、客户端证书及密钥说明

本文章对应的文档：使用OpenSSL创建生成CA证书服务器客户端证书及密钥资源-CSDN文库 https://download.csdn.net/download/weixin_41885845/88746920 对于SSL单向认证 服务器需要CA证书、server证书、server私钥，客户端需要CA证。 对于SSL双向认证 服务器需要CA证书、serv…
阅读更多...
基于人工蚁群、蚁群、遗传算法的多目标任务分配

基于人工蚁群、蚁群、遗传算法的多目标任务分配

matlab2020a可运行 基于人工蚁群、蚁群、遗传算法的多目标任务分配资源-CSDN文库
阅读更多...
VBA窗体跟随活动单元格【简易版】(2/2)

VBA窗体跟随活动单元格【简易版】(2/2)

上一篇博客&#xff08;文章连接如下&#xff09;中使用工作表事件Worksheet_SelectionChange实现了窗体跟随活动单元格的动态效果。 VBA窗体跟随活动单元格【简易版】(1/2) 为了在用户滚动工作表窗体之后仍能够实现跟随效果&#xff0c;需要使用Application.Windows(1).Visibl…
阅读更多...
010-新手如何建立一个属于自己的图像处理FPGA/ZYNQ框架（自己的用着才舒服，内容非常全面！）

010-新手如何建立一个属于自己的图像处理FPGA/ZYNQ框架（自己的用着才舒服，内容非常全面！）

文章目录 前言一、图像处理框架二、图像采集输入1.常用视频流格式&#xff1a;Rgb565/Bayer1.RGB565数据流格式2.Bayer阵列数据流格式 2.图像预处理&#xff1a;时钟域同步/去马赛克/色彩空间转换/滤波1.时钟域同步2.图像去马赛克化3.色彩空间转换4.滤波 三、图像算法处理1.图像…
阅读更多...
P9847 [ICPC2021 Nanjing R] Crystalfly 题解 （SPJ）

P9847 [ICPC2021 Nanjing R] Crystalfly 题解 （SPJ）

[ICPC2021 Nanjing R] Crystalfly 传送门&#xff1f; 题面翻译 给定一个 n ( 1 ≤ n ≤ 1 0 5 ) n(1\le n\le10^5) n(1≤n≤105) 个节点的树&#xff0c;每个节点上有 a i a_i ai​ 只晶蝶。派蒙最初在 1 1 1 号节点&#xff0c;并获得 1 1 1 号节点的所有晶蝶&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023