
🎉欢迎您来到我的MySQL基础复习专栏
☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克🍹
✨博客主页:小小恶斯法克的博客
🎈该系列文章专栏:重拾MySQL-进阶篇
🍹文章作者技术和水平很有限,如果文中出现错误,希望大家能指正🙏
📜 感谢大家的关注! ❤️

目录
🚀索引概述
🚀索引的特点
🚀索引结构
🚀二叉树
🚀红黑树
🚀B树:为磁盘而生
🚀B树的构建 (这里引用的是一个博主的构建过程,我觉得还不错http://t.csdnimg.cn/3VtX2)
🚀B+Tree (以下这里引用了黑马部分)
🚀Hash
🚀为什么InnoDB存储引擎选择使用B+tree索引结构?
🚀索引概述
索引(index)是帮助MySQL高效获取数据的数据结构(有序)。数据库系统还维护着满足 特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据,这样就可以在这些数据结构 上实现高级查找算法,这种数据结构就是索引。
索引说明:
假设我们要执行的SQL语句是:select * from emp where age = 43 ;
✨无索引
在无索引情况下,就需要从第一行开始扫描,一直扫描到最后一行,我们称之为全表扫描,性能很低。

✨有索引
如果我们针对于这张表建立了索引,假设索引结构就是二叉树,那么也就意味着,会对age这个字段建立一个二叉树的索引结构。

此时我们在进行查询时,只需要扫描三次就可以找到数据了,极大的提高的查询的效率。
注意:这里我们只是假设索引的结构是二叉树,介绍一下索引的大概原理,只是一个示意图,并不是索引的真实结构,索引的真实结构通常是基于B树或者B+树
🚀索引的特点
| 特点 | 优点 | 缺点 |
| 提高检索速度 | 加快数据的检索速度,特别是对大表进行检索时 | 增加了写操作的时间,因为每次插入、更新和删除都需要维护索引 |
| 唯一约束 | 可以确保列或列组合的唯一性 | 唯一索引会增加写操作的开销 |
| 加速排序 | 在使用ORDER BY子句进行排序时可以加快查询速度 | 占用额外的磁盘空间 |
| 加速分组和联接 | 对于GROUP BY和JOIN操作,索引可以提高查询性能 | 不恰当的索引可能导致查询性能下降 |
| 全文搜索 | 允许对文本字段进行高效的全文搜索 | 需要额外的存储空间,并且不支持所有的数据类型 |
| 减少IO成本 | 可以减少磁盘IO的次数,提高查询效率 | 创建和维护索引需要额外的计算资源 |
🚀索引结构
MySQL的索引是在存储引擎层实现的,不同的存储引擎有不同的索引结构,主要包含以下几种:
| 索引结构 | 描述 |
| B+Tree索引 | 最常见的索引类型,大部分引擎都支持 B+ 树索引 一种自平衡的多路搜索树,所有关键字都存储在叶子节点上,并且叶子节点之间通过指针连接形成有序链表。非叶子节点只包含键值信息,不包含实际数据。适用于范围查找,对于数据库系统来说更加适用。 |
| Hash索引 | 底层数据结构是用哈希表实现的 , 只有精确匹配索引列的查询才有效 , 适用于等值查找,不支持范围查询 |
| R-tree(空间索引) | 空间索引是MyISAM引擎的一个特殊索引类型,主要用于地理空间数据类 型,通常使用较少 |
| Full-text(全文索引 ) | 是一种通过建立倒排索引 ,快速匹配文档的方式。类似于 Lucene,Solr,ES 用于全文搜索的索引结构,支持对文本字段进行高效的全文搜索,适用于大段文本的搜索。 |
上述是MySQL中所支持的所有的索引结构,接下来,我们再来看看不同的存储引擎对于索引结构的支持情况。
| 索引 | InnoDB | MyISAM | Memory |
| B+tree索引 | 支持 | 支持 | 支持 |
| Hash 索引 | 不支持 | 不支持 | 支持 |
| R-tree 索引 | 不支持 | 支持 | 不支持 |
| Full-text | 5.6版本之后支持 | 支持 | 不支持 |
注意:我们平常所说的索引,如果没有特别指明,都是指B+树结构组织的索引。
🚀二叉树
二叉树具有以下性质:左子树的键值小于根的键值,右子树的键值大于根的键值。
如下图所示就是一棵二叉查找树,
假如说MySQL的索引结构采用二叉树的数据结构,理想状态下结构是:
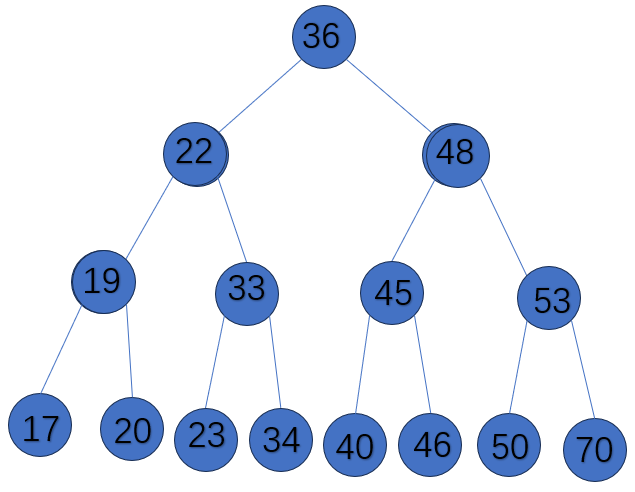
如果主键是顺序插入的,则会形成一个单向链表:

所以,如果选择二叉树作为索引结构,会存在以下缺点:
✨顺序插入时,会形成一个链表,查询性能大大降低。
✨大数据量情况下,层级较深,检索速度慢。
🚀红黑树
此时大家可能会想到,我们可以选择红黑树,红黑树是一颗自平衡二叉树,那这样即使是顺序插入数 据,最终形成的数据结构也是一颗平衡的二叉树 ,结构如下 :
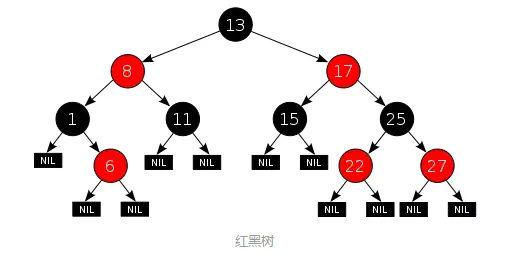
✨对于数据在内存中的情况(如上述的TreeMap和HashMap),红黑树的表现是非常优异的。但是对于数据在磁盘等辅助存储设备中的情况(如MySQL等数据库),红黑树并不擅长,因为红黑树长得还是太高了。当数据在磁盘中时,磁盘IO会成为最大的性能瓶颈,设计的目标应该是尽量减少IO次数;而树的高度越高,增删改查所需要的IO次数也越多,会严重影响性能。
✨所以,在MySQL的索引结构中,并没有选择二叉树或者红黑树,而选择的是B+Tree,那么什么是 B+Tree呢?在详解B+Tree之前,先来介绍一个B-Tree。
🚀B树:为磁盘而生
B-Tree, B树是一种多叉路衡查找树,相对于二叉树, B树每个节点可以有多个分支,即多叉。
以一颗最大度数(max-degree)为5(5阶)的b-tree为例,那这个B树每个节点最多存储4个key,5
个指针:
✨B树,也是自平衡的排序查找树,但是不要求子节点数目必须小于2。
✨每个节点可以有最多M个子节点,M>=2,M即为B树的阶数
✨每个节点中可以存储最多M个、最少M/2向上取整个key,一般为2-3个。
✨所有叶子节点均在同一层
树的度数指的是一个节点的子节点个数。
还有一个更详细的图:
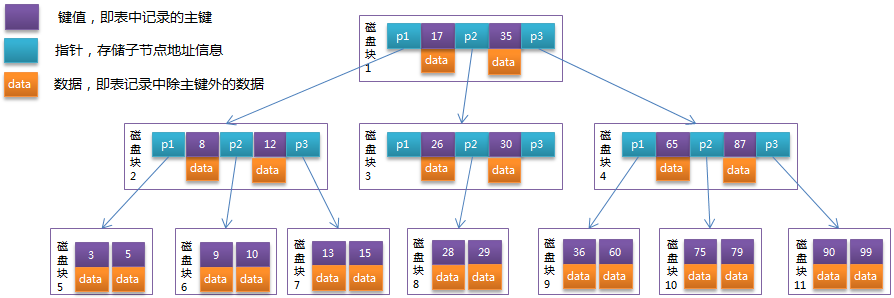
🚀B树的构建 (这里引用的是一个博主的构建过程,我觉得还不错http://t.csdnimg.cn/3VtX2)
B树的构建过程中每个节点中的关键字的个数都在动态改变。
因为其构建过程是:先对节点先扩充,当节点中关键字数量扩充到等于M时,再对其进行拆分,并将中间数升到父节点中去。
例如:定义一个5阶树(平衡5路查找树;),现在我们要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来;
遵循规则:
(1)节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分);当节点中关键字数大于4时,就将中间的关键字升为父节点的关键字(如果没有父节点,则创建一个父节点),然后创建此父节点的两个子节点,将中间关键字两边的关键字分别存储到这两个子节点中。
(2)排序规则:满足节点本身比左边节点大,比右边节点小的排序规则;
先插入 3、8、31、11
再插入23、29再插入50、28
特点:
✨5阶的B树,每一个节点最多存储4个key,对应5个指针。
✨一旦节点存储的key数量到达5,就会裂变,中间元素向上分裂。
✨在B树中,非叶子节点和叶子节点都会存放数据。
🚀B+Tree (以下这里引用了黑马部分)
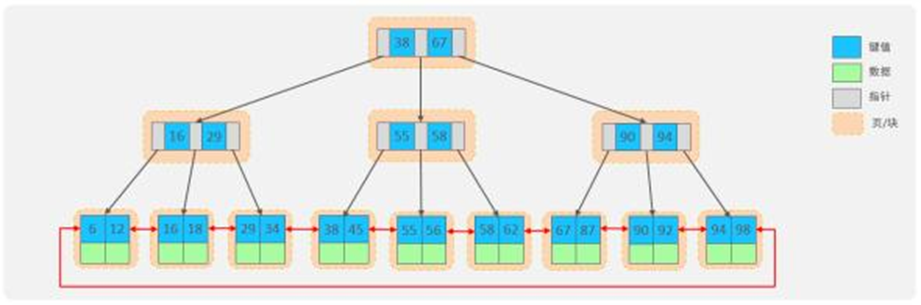
B+Tree是B-Tree的变种,我们以一颗最大度数(max-degree)为4 (4阶)的b+tree为例,来看一 下其结构示意图:
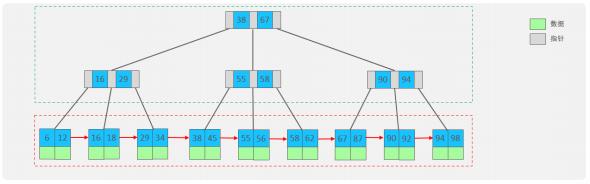
我们可以看到,两部分:
✨绿色框框起来的部分,是索引部分,仅仅起到索引数据的作用,不存储数据。
✨红色框框起来的部分,是数据存储部分,在其叶子节点中要存储具体的数据。
插入一组数据:100 65 169 368 900 556 780 35 215 1200 234 888 158 90 1000 88 120 268 250 。然后观察一些数据插入过程中,节点的变化情况。

最终我们看到,B+Tree 与 B-Tree相比,主要有以下三点区别:
✨所有的数据都会出现在叶子节点。
✨叶子节点形成一个单向链表。
✨非叶子节点仅仅起到索引数据作用,具体的数据都是在叶子节点存放的。
上述我们所看到的结构是标准的B+Tree的数据结构,接下来,我们再来看看MySQL中优化之后的 B+Tree。
✨MySQL索引数据结构对经典的B+Tree进行了优化。在原B+Tree的基础上,增加一个指向相邻叶子节点 的链表指针,就形成了带有顺序指针的B+Tree,提高区间访问的性能,利于排序。
🚀Hash
✨MySQL中除了支持B+Tree索引,还支持一种索引类型---Hash索引。
✨哈希索引就是采用一定的hash算法,将键值换算成新的hash值,映射到对应的槽位上,然后存储在hash表中。
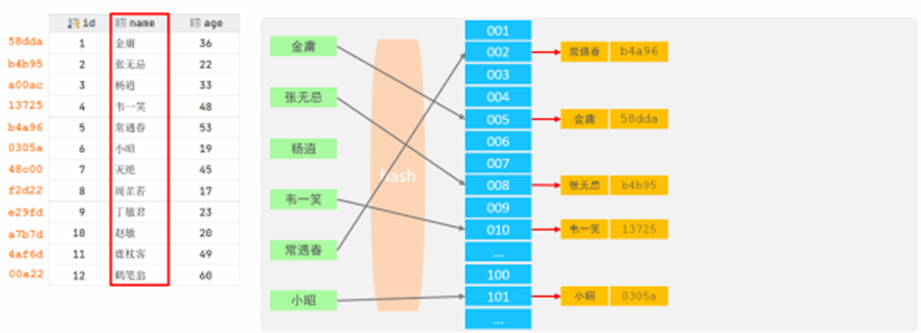
如果两个(或多个)键值,映射到一个相同的槽位上,他们就产生了hash冲突(也称为hash碰撞),可 以通过链表来解决。
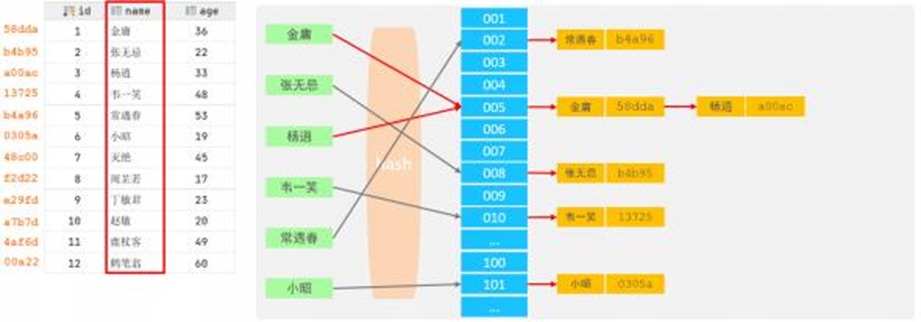
✨Hash索引只能用于对等比较 (=, in),不支持范围查询(between, >, < , ...)
✨无法利用索引完成排序操作
✨查询效率高,通常(不存在hash冲突的情况)只需要一次检索就可以了,效率通常要高于B+tree索引
存储引擎支持
在MySQL中,支持hash索引的是Memory存储引擎。 而InnoDB中具有自适应hash功能, hash索引是 InnoDB存储引擎根据B+Tree索引在指定条件下自动构建的。
🚀为什么InnoDB存储引擎选择使用B+tree索引结构?
✨平衡的高效查找: B+树具有平衡性,使得在大数据量情况下,查询操作的时间复杂度保持在较低水平(通常为O(log n))。
✨多路搜索: B+树的多路搜索特性使得每一步操作都能跳过大量的数据,从而提高了查询效率。
✨对于B-tree,无论是叶子节点还是非叶子节点,都会保存数据,这样导致一页中存储 的键值减少,指针跟着减少,要同样保存大量数据,只能增加树的高度,导致性能降低;
✨相对Hash索引, B+tree支持范围匹配及排序操作
(范围查询: B+树索引结构天生适合范围查询,因为其内部有序排列的特性可以快速定位到范围的起始点,并且进行连续的遍历。
顺序访问: B+树的叶子节点形成有序链表,这使得对整个表进行顺序扫描时非常高效。)
希望对你有帮助!

![[力扣 Hot100]Day7 接雨水](https://img-blog.csdnimg.cn/direct/31cfe09692c34bdfa031bd7fe5323b7c.png)


![[bat]0基础实现自动化办公-基于start实现一键打开常用软件/文档](https://img-blog.csdnimg.cn/direct/2a3e846a658d41acb7e20a1a488738ad.png)