之前一篇文章介绍了" 数组和链表"，今天继续介绍"栈和队列"。

栈

我们先来看一个有趣的现象。

• 首先打开"百度"随意搜索一个名词
  

• 点击"视频"
  

• 点击"文库"
  

• 点击"<-“箭头，看看会发生什么。回退到了"视频"页面并且出现了”->"箭头。
  

• 再次点击"<-“箭头，依然会回退到上一个页面"网页”。如果点击"->“箭头则会前进到下一个页面"文库”。这里就不演示了。

• 此时点击"图片"看看会发生什么。"->"箭头消失了。
  

• 点击"<-“箭头，回退到了"视频页面”。再点击"<-"箭头回退到了"网页"页面，但是"文库"页面丢失了，找不到了。

• 这是怎么实现的呢？我们一起来看看吧

栈的概述

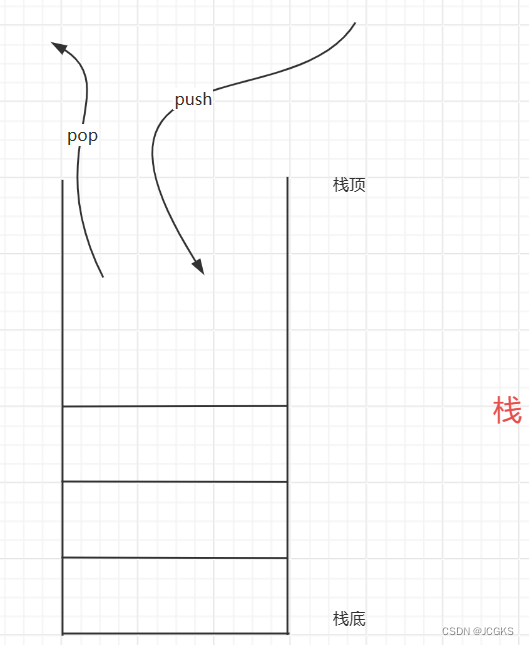
上一篇文章提到过，栈和队列都是操作受限的线性表。栈只允许在线性表的一端进行删除和增加操作，另外一端是封闭的状态。就像是一摞叠在一起的盘子，放的时候只能从下往上一个一个放；取的时候，从上往下一个一个取；既不能从中间放也不能从中间抽取；像这种"先进后出，后进先出"的结构就是栈。

栈的实现

栈既可以基于数组实现，也可以基于链表实现。用数组实现的栈叫做顺序栈，用链表实现的栈叫做链式栈。
栈的基本操作有以下几个

• 判断栈是否为空
• 判断栈是否已满[链式栈无需判断，顺序栈需要判断]
• 获取栈的元素个数
• 获取栈顶元素
• 入栈
• 出栈

以下是一个简单的顺序栈的实现

#include<iostream>
using namespace std;template <typename T>
class mystack{
public:mystack(int _c):cap(_c),in(0),st(new T[_c]){}~mystack(){delete []st;}bool empty();int size();bool full();void push(T);void pop();T top();
private:int cap;//the cap of stackint in;//the top of stackT *st;
};
template <typename T>
bool mystack<T>::empty(){return this->in==0;
}
template <typename T>
int mystack<T>::size(){return this->in;
}
template <typename T>
bool mystack<T>::full(){return this->in==this->cap;
}template <typename T>
void mystack<T>::push(T a){st[this->in++]=a;
}
template <typename T>
void mystack<T>::pop(){--this->in;
}template <typename T>
T mystack<T>::top(){return st[in-1];
}    

如果想要实现动态扩容栈，就让底层的数组实现动态扩容即可。

栈在函数调用中的应用

栈作为一个比较基础的数据结构，应用场景很多。其中，比较经典的一个应用场景就是函数调用栈[也是递归程序实现的基础]。
操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成"栈"这种结构，用来存储函数调用时的局部变量也称之为临时变量。每进入一个函数之前，就会将调用者作为一个栈帧入栈，当被调用函数执行完之后，将这个函数对应的栈帧出栈。

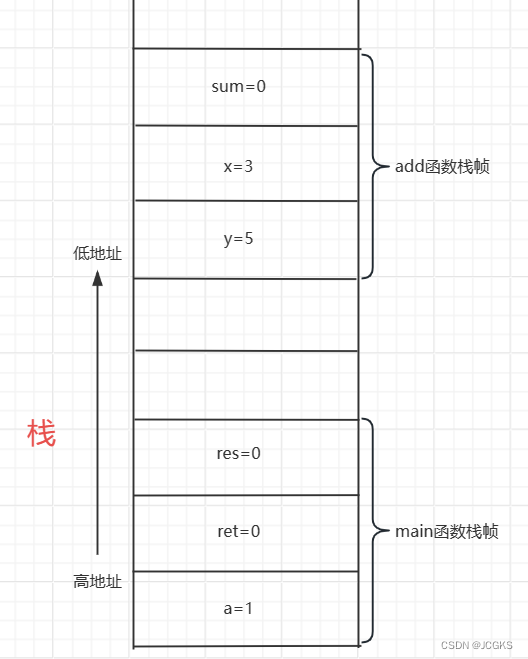
为了更好的理解栈在函数中调用中的应用，观察下面的程序，main函数调用add函数，返回数值存储到变量ret，变量a与ret相加存储到res变量，最后打印res的数值。

int main() {int a = 1; int ret = 0;int res = 0;ret = add(3, 5);res = a + ret;printf("%d", res);reuturn 0;
}
int add(int x, int y) {int sum = 0;sum = x + y;return sum;

以下是main函数调用add函数时，函数调用栈的情况。

栈在表达式求值中的应用

为了方便解释，将算术表达式简化为只包含加减乘除四则运算，比如"13+3*9+44-24/4"。对于这个四则运算，人脑可以很快地求解出答案，但是对于计算机来说，理解这个表达式本身就很困难。那我们该如何编写程序才能让计算机理解呢？需要借助什么样的数据结构呢？

实际上，可以通过两个栈来实现。一个用来保存操作数称之为操作数栈，另一个用来保存运算符称之为运算符栈，乘除的运算优先级高于加减。从左向右遍历表达式，当遇到数字，直接压入操作数栈；遇到运算符，先与运算符栈顶运算符进行比较：如果比运算符栈顶运算符的优先级高，就将当前运算符压栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取出两个操作数，然后进行计算，在把计算完的结果压入操作数栈，继续上述的步骤直到当前运算符优先级高于栈顶运算符优先级。

这里有一个小细节需要注意：栈结构的特点是"先进后出"，所以从操作数栈取出的第一个整数是运算符右边的操作数，取出的第二个操作数才是运算符左边的操作数。对于"+“操作，不必特别区分左右操作数，但是对于”-,*,/"操作必须要区分左右操作数，否则会计算出错。

为了加深理解，对于表达式"5+3*8-8"的计算过程，画成了一张图，如下所示。

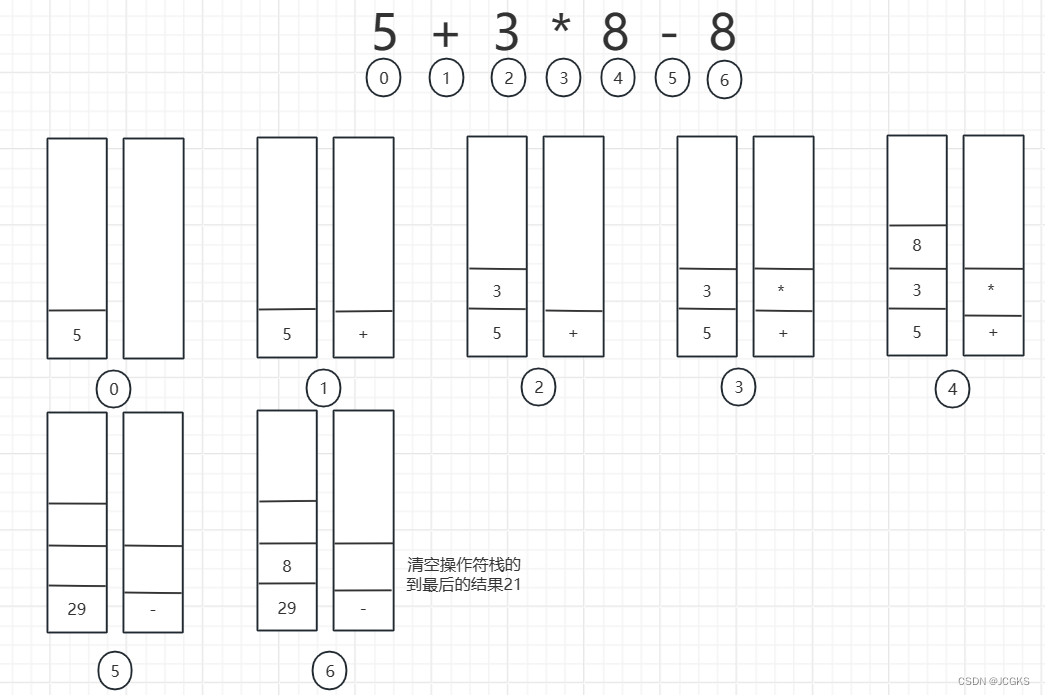
• 第五个步骤。遇到运算符’-‘，优先级低于"*"，取出操作数"8[右操作数]和3[左操作数]"进行乘法运算的24，将24压入操作数栈。’-‘优先级等于’+'，取出操作数"24和5"进行加法运算的29，29重新压入操作数栈。
• 第六个步骤。取出操作数"8[右操作数]和29[左操作数]"进行减法操作，得到最后结果21.

分析完了"栈在表达式求值中的作用"，来做一道算法题吧

逆波兰表达式求值

https://leetcode.cn/problems/evaluate-reverse-polish-notation/description/

由于给定的表达式是一个后缀表达式所以只需要一个操作数栈即可
后缀表达式：是指运算符在操作数的后边，按顺序遍历遇到操作数进栈，遇到运算符直接出栈取数运算即可。

class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> nums;//操作数栈int left,right,sum;//左右操作数和计算结果for(const string&to:tokens){if(!(to=="+" || to=="-" || to=="*" || to=="/")){//数字int te =stoi(to);nums.push(te);continue;}right = nums.top();nums.pop();left = nums.top();nums.pop();if(to=="+"){sum=left+right;}else if(to=="-"){sum=left-right;}else if(to=="*"){sum=left*right;}else if(to=="/"){sum=left/right;}nums.push(sum);}return nums.top();}
};

func evalRPN(tokens []string) int {//用切片模拟栈st:=make([]int,0,len(tokens))var left,right,sum intfor _,to:=range tokens{if !(to=="+" || to=="-" || to=="*" || to=="/"){te,_:=strconv.Atoi(to)st=append(st,te)continue}right = st[len(st)-1]left = st[len(st)-2]st=st[:len(st)-2]if to=="+"{sum=left+right}else if to=="-"{sum=left-right}else if to=="*"{sum=left*right}else if to=="/"{sum=left/right}st=append(st,sum)}return st[0]
}

栈在括号匹配中的应用

除了用栈实现表达式求值，还可以借助栈检查表达式中的括号是否匹配。

假设括号的类型只有三种：圆括号()、方括号[]、花括号{}，并且它们可以任意嵌套。比如{[()]}、[({}),{()}]等都为合法格式，但是[(}]、[{})等是不合法的格式。那我们如何检查一个括号是否是合法的格式呢?

这里也可以使用栈解决。用栈保存未匹配的左括号，从左到右依次扫描字符串。扫描到左括号入栈，扫描到右括号从栈顶取出一个左括号，如果左右括号不匹配则括号不合法，如果合法继续向后扫描。扫描完之后发现栈不为空则括号不合法[左括号比右括号多]，反之则合法。

为了方便理解，对于括号"[({})]"的合法性验证，画成如下一张图

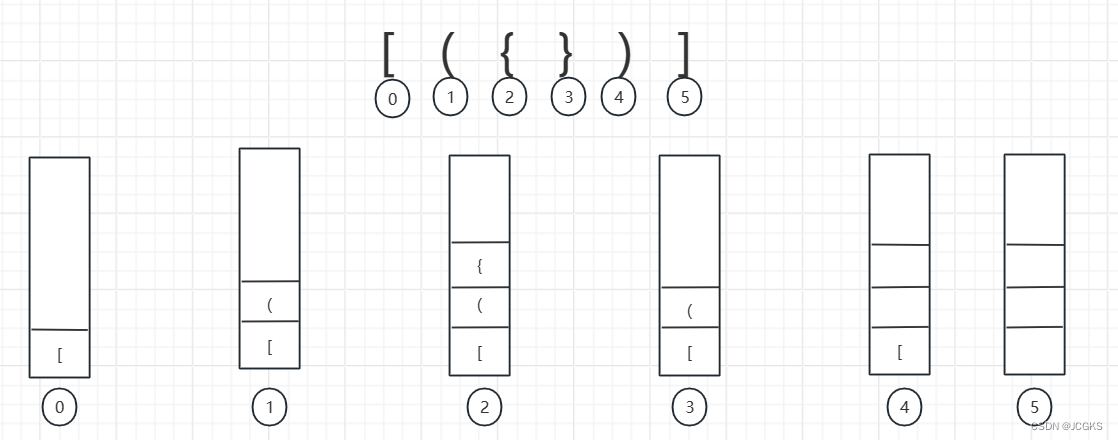
• 推算到最后栈为空，括号合法

分析完了"栈在括号匹配中的作用"，来做一道算法题吧

有效的括号

https://leetcode.cn/problems/valid-parentheses/description/

class Solution {
public:bool isValid(string s) {stack<char> st;char te;for (const char&ss:s){if(ss=='[' || ss=='(' || ss=='{') st.push(ss);else {if(st.empty()) return false;te=st.top();st.pop();if(ss==']'){if(te!='[') return false;}else if(ss==')'){if(te!='(') return false;}else if(ss=='}'){if(te!='{') return false;}}}return st.empty();}
};

func isValid(s string) bool {//用slice模拟栈st:=make([]rune,0,len(s))for _,ss:=range s{if ss=='[' || ss=='(' || ss=='{'{st=append(st,ss)}else{if len(st)==0 {return false}te:=st[len(st)-1]st = st[:len(st)-1]switch ss{case ']':if te!='[' {return false}case ')':if te!='(' {return false}case '}':if te!='{' {return false}default:}}}return len(st)==0
}

最长的有效括号

https://leetcode.cn/problems/longest-valid-parentheses/

思路：

• 除了要考虑左右括号是否匹配之外，还需要考虑这些匹配的括号是否连续，连续的话累加计数，不连续的话重新计数。从左向右遍历，有一下两种情况：
• 遇到的是"("。左括号必须要找到匹配的右括号才能够算是一对有效的括号，所以直接将其入栈等待被匹配。
• 遇到的是")“。栈顶元素出栈，如果栈顶元素是”("则找到一对有效的括号。

以上只是简单的思路，现在考虑一些需要注意的细节。

• 由于有效括号要求格式正确且连续，为了连续我们不能只是简单的判断左右括号是否匹配，还需要考虑它们所在的位置也就是下标。那不妨存储括号的下标而不是括号本身[因为括号无非两种"(“或者”)"]。
• 当遇到的是"("将其下标存储在栈中。
• 当遇到的是")"。直接出栈，说明找到一对有效括号。此时有效括号的长度就是i-st.top。出栈之后栈空需要将当前的下标入栈。[出现这种情况就是右括号比左括号多]
• 为了考虑")“、”()"的特殊情况，需要在开始的时候将-1入栈。

class Solution {
public:int longestValidParentheses(string s) {stack<int> st;st.push(-1);int len=0;for(int i=0;i<s.size();++i){if(s[i]=='('){st.push(i);}else {st.pop();if(st.empty()) {st.push(i);}else{len=max(len,i-st.top());}}}return len;}
};

func longestValidParentheses(s string) int {st:=make([]int,0,len(s))st=append(st,-1)maxlen:=0for i,_:=range s{if s[i]=='('{st=append(st,i)}else {st=st[:len(st)-1]if len(st)==0{st=append(st,i)}else {maxlen=max(maxlen,i-st[len(st)-1])}}}return maxlen
}
func max(a,b int)int{if a>b{return a}return b
}

删除字符串中的所有相邻重复项

class Solution {
public:string removeDuplicates(string s) {stack<char> st;for(const char&ss:s){if (st.empty() || ss!=st.top()) st.push(ss);else while(!st.empty()&&ss==st.top()) st.pop();}string ans(st.size(),' ');int in = st.size()-1;while(!st.empty()) {ans[in--]=st.top();st.pop();}return ans;}
};

func removeDuplicates(s string) string {st:=make([]int32,0,len(s))for _,ss:=range s{if len(st)==0 || ss!=st[len(st)-1] {st=append(st,ss)}else{for len(st)!=0 && ss==st[len(st)-1]{st=st[:len(st)-1]}}}res:=""for _,ss:=range st{res+=string(ss)}return res
}

如何获取栈内最小元素呢

由于栈结构"先进后出"的特性，决定了访问栈内的元素必须按照顺序，并且每访问一个元素都需要将其从栈中丢弃，才能继续访问下一个元素，那对于这种操作受限的结构无法直接遍历，该如何找到最小的元素呢。

实际上可以使用两个栈来解决，假设现有A、B两个栈。

• 新元素加入先加入到A栈；
• 要想获取到栈内最小元素需要借助辅助栈B。新元素加入到A栈的同时，将其加入到B栈。若B栈为空直接加入，否则元素小于等于栈顶元素直接入栈，大于栈顶元素忽略。
• 出栈操作。从A栈出栈元素，如果A出栈的元素和B栈栈顶元素吻合，B栈也要执行出栈操作，反之不用。

为了帮助理解我画了一张演示图

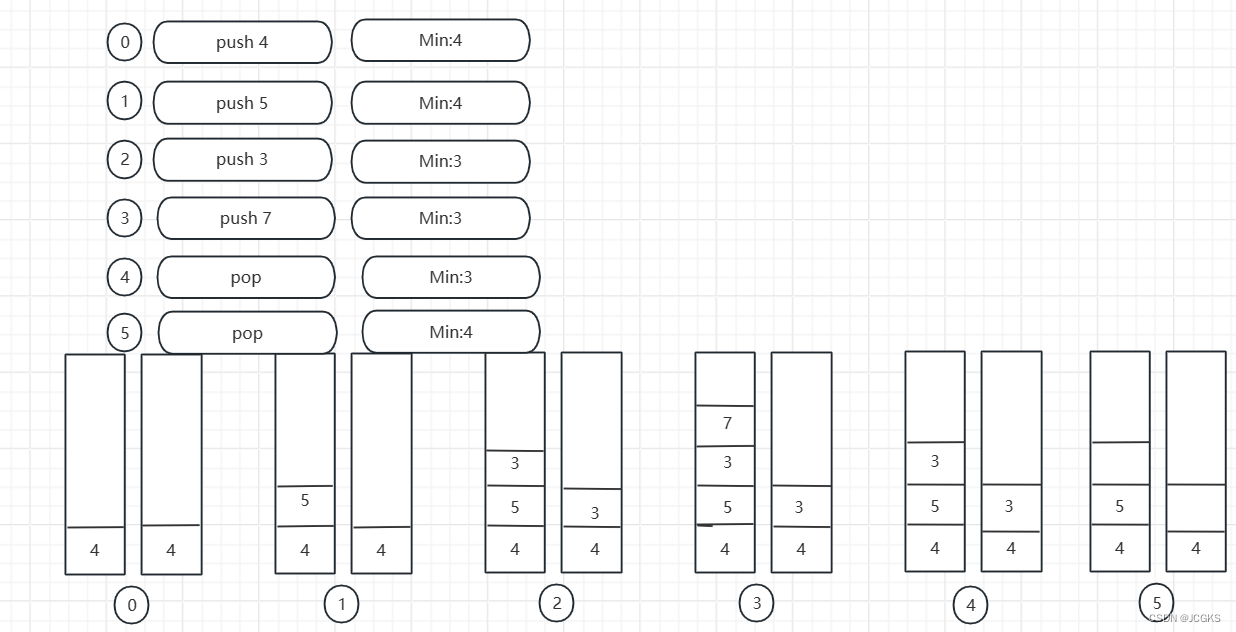
理解了上述的思路我们来编程实现一下
https://leetcode.cn/problems/bao-han-minhan-shu-de-zhan-lcof/description/

class MinStack {
public:/** initialize your data structure here. */MinStack() {}void push(int x) {a.push(x);if(b.empty() || x<=b.top()) b.push(x);}void pop() {int x=a.top();a.pop();if (x==b.top()) b.pop();}int top() {if(a.empty()) return -1;return a.top();}int getMin() {return b.top();}
private:stack<int>a;stack<int>b;
};

type MinStack struct {a,b []int
}/** initialize your data structure here. */
func Constructor() MinStack {return MinStack{a:[]int{},b:[]int{},}
}func (this *MinStack) Push(x int)  {this.a=append(this.a,x)if len(this.b)==0 || x<=this.b[len(this.b)-1] {this.b=append(this.b,x)}
}func (this *MinStack) Pop()  {x:=this.a[len(this.a)-1]this.a=this.a[:len(this.a)-1]if x==this.b[len(this.b)-1]{this.b=this.b[:len(this.b)-1]}
}func (this *MinStack) Top() int {return this.a[len(this.a)-1]}func (this *MinStack) GetMin() int {return this.b[len(this.b)-1]}

如何实现浏览器的前进和后退

看到这里相信你已经了解了栈的概念和特性。那现在来分析如何实现开头说的那个有趣的现象。

• 实际上，可以使用两个栈来实现。
• 使用两个栈X和Y，把首页浏览的页面a,b,c依次压入栈X，当点击后退按钮时，再依次从栈X中出栈并加入栈Y。当点击前进按钮时，依次从栈Y中取出数据并加入栈X。栈X中没有数据不能再进行后退，栈Y中没有数据不能进行前进。

接下来用图演示一下

• 假设顺序查看了a,b,c三个页面，依次把a,b,c压入栈中。两个栈的数据如下

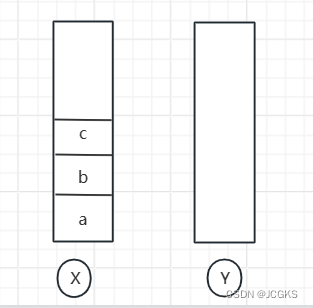
• 通过浏览器的后退按钮，从页面c回退到页面a，旧依次把b\c从x栈中弹出，依次放入到y栈中。两个栈的数据如下：

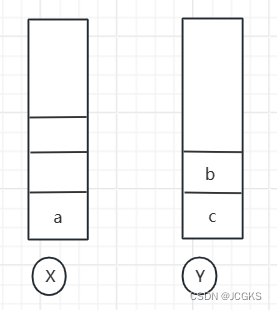
• 这个时候想看页面b,于是点击前进按钮进入到页面b。此时两个栈的数据如下所示

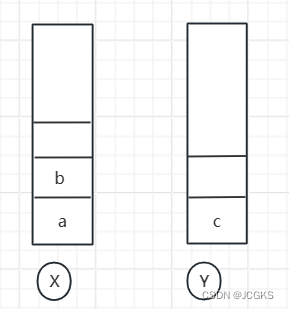
• 这个时候通过页面b跳转到页面e，这个时候Y栈被清空了，所以页面c就找不到了。两个栈的数据如下

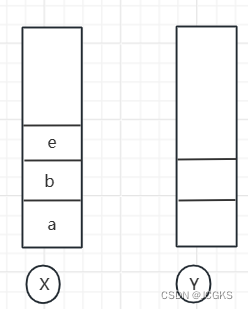
队列

进入正题之前，先考虑这样一个问题。计算机一旦启动，就无时无刻不在处理着任务。例如，打开某个应用程序，点击某个页面，点击某个图片，向键盘敲下的每一个字符等等，对计算机来说都是一系列的任务。那计算机该如何处理这些任务的，学过操作系统的都知道，计算机会为每一个任务分配一个线程。那么任务的处理速度与线程的数量成正比吗？实际上并不是的，因为线程需要得到CPU的调度，但是CPU的资源是有限的，过多的线程还会导致频繁的上下文切换，导致效率低下。所以引入了线程池，也即是一个固定大小的池子中有一定数量的创建好的线程，这一步是为了减少线程频繁创建和销毁的开销。当向固定大小的线程池中请求一个线程时，如果线程池中没有空闲的资源，这个时候线程池该如何处理这个请求?是拒绝请求还是排队请求?各种处理策略又是如何实现的？带着这些疑问，学习队列吧

队列的定义

队列与栈一样都是操作受到限制的线性表，队列是一种"先进先出，后进后出"的结构，就像是排队买糕点，先来的人先买到后来的人后买到。入队的时候从队尾进入，出队的时候从队头出去。

下图把"队列和栈"放在一起对比

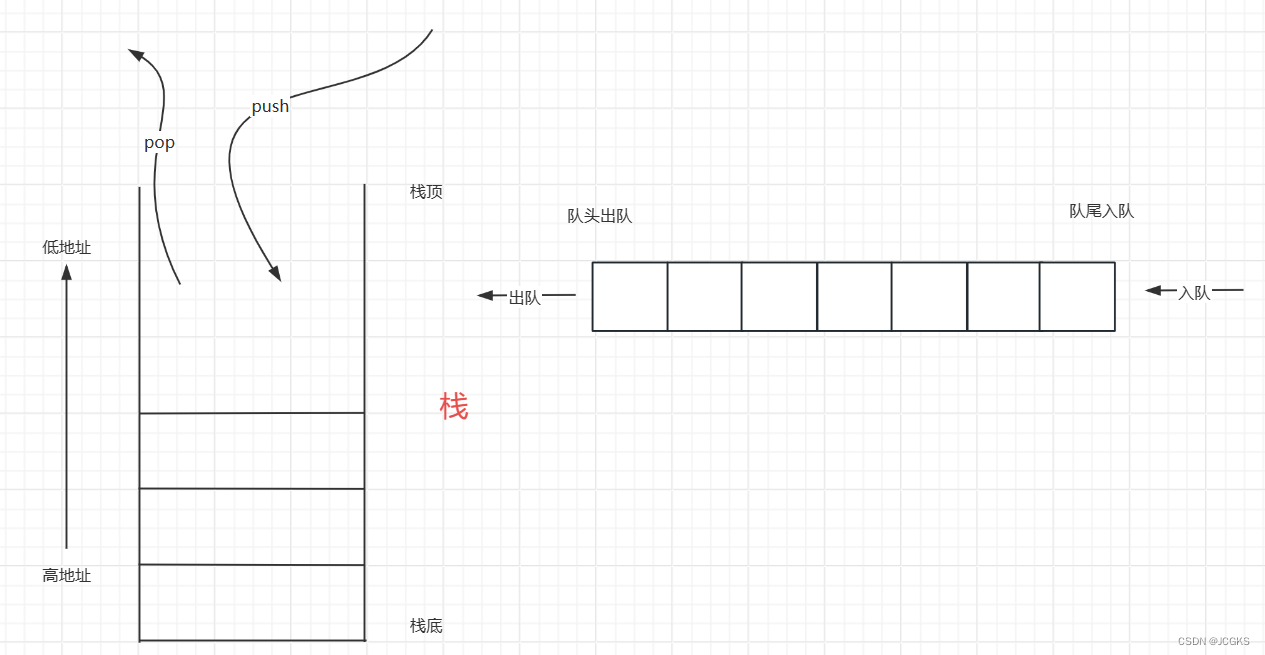
队列的实现

队列和栈一样，也有顺序队列和链式队列两种实现。一些基本操作如下：

• 判断队列是否为空
• 判断队列是否已满[链式队列无需判断]
• 获取队头元素
• 入队
• 出队
• 获取队列元素总数

以下是是一个顺序队列的实现

#include<iostream>
using namespace std;template <typename T>
class mystack{
public:mystack(int _c):cap(_c),head(0),tail(0),st(new T[_c]){}~mystack(){delete[] st;}bool empty();bool full();int size();void push(T);void pop();T front();
private:int cap;//the cap of stackint head,tail;T *st;
};
template <typename T>
bool mystack<T>::empty(){return tail==0;
}
template <typename T>
bool mystack<T>::full(){return tail==cap;
}
template <typename T>
int mystack<T>::size(){return tail-head+1;
}template <typename T>
void mystack<T>::push(T a){st[tail++]=a;
}
template <typename T>
void mystack<T>::pop(){++head;
}template <typename T>
T mystack<T>::top(){return st[head];
}

• 从代码中可以发现，这样的实现方式有一定的弊端：刚开始一直向队尾添加元素直到队列满，此时从队头出队元素直到元素都出队。此时再向队列中添加元素，由于"判断出栈是满的"而无法将元素入队。
• 可以发现这样的实现方式，非常浪费空间。打个比方，就像是排队去买冰激淋，每服务完一个客户，店家就像前走一步服务下一个客户，这样就导致有能力服务更多客户的时候，却因为没有位置而失去这些客户。
• 那根据生活中的尝试，前一个客户走了，后面的客户向前移动不久好了。理论上这样做没错，但是如果元素很多的时候会是不小的开销，如果频繁的执行出队元素，这样的开销更大。
• 为了解决上述两种实现方案的弊端，引入了循环队列

循环队列

"循环队列"顾名思义就是，队头队尾相连接形成一个环状的结构。接下来看看如何实现吧

• 设置循环队列有一个需要注意的点，队列为空的时候队列的头尾指针重合，队列满的时候队列的头尾指针也重合，所以需要一些特殊的标识区分两种情况。
• 第一种方法就是，设置一个变量size表示队列中的元素个数，如果头尾指针重合的时候size达到队列的容量那么队列是一种满的状态，否则就是空的状态。
• 第二种方法就是，将队列的一个位置空出来不存储任何元素，这样当头尾指针重合就是队列空的状态，尾指针的下一个位置是头指针就是满的状态。[由于空出一个位置，所以如果队列需要多申请一块空间]

https://leetcode.cn/problems/design-circular-queue/description/

size变量

class MyCircularQueue {
public:MyCircularQueue(int k):cap(k),size(0),head(0),tail(0),buf(new int[k]) {}~MyCircularQueue(){delete []buf;}bool enQueue(int value) {if(isFull()) return false;buf[tail]=value;tail=(tail+1)%cap;++size;return true;}bool deQueue() {if(isEmpty()) return false;head=(head+1)%cap;--size;return true;}int Front() {if(isEmpty()) return -1;return buf[head];}int Rear() {if(isEmpty()) return -1;return buf[(tail-1+cap)%cap];}bool isEmpty() {return head==tail && size==0;}bool isFull() {return head==tail && size==cap;}
private:int cap;int size;int head,tail;int *buf;
};

type MyCircularQueue struct {cap,size inthead,tail intbuf []int
}func Constructor(k int) MyCircularQueue {return MyCircularQueue{cap:k,size:0,head:0,tail:0,buf:make([]int,k),}
}func (this *MyCircularQueue) EnQueue(value int) bool {if this.IsFull(){return false}this.buf[this.tail]=valuethis.tail=(this.tail+1)%this.capthis.size++return true
}func (this *MyCircularQueue) DeQueue() bool {if this.IsEmpty(){return false}this.head=(this.head+1)%this.capthis.size--return true
}func (this *MyCircularQueue) Front() int {if this.IsEmpty() {return -1}return this.buf[this.head]
}func (this *MyCircularQueue) Rear() int {if this.IsEmpty() {return -1}return this.buf[(this.tail-1+this.cap)%this.cap]
}func (this *MyCircularQueue) IsEmpty() bool {return this.head==this.tail && this.size==0
}func (this *MyCircularQueue) IsFull() bool {return this.tail ==this.head && this.size==this.cap
}

空出一个位置

class MyCircularQueue {
public:MyCircularQueue(int k):size(k+1),head(0),tail(0),buf(new int[k+1]) {}~MyCircularQueue(){delete []buf;}bool enQueue(int value) {if(isFull()) return false;buf[tail]=value;tail=(tail+1)%size;return true;}bool deQueue() {if(isEmpty()) return false;head=(head+1)%size;return true;}int Front() {if(isEmpty()) return -1;return buf[head];}int Rear() {if(isEmpty()) return -1;return buf[(tail-1+size)%size];}bool isEmpty() {return head==tail;}bool isFull() {return (tail+1)%size == head;}
private:int size;int head,tail;int *buf;
};

type MyCircularQueue struct {cap inthead,tail intbuf []int
}func Constructor(k int) MyCircularQueue {return MyCircularQueue{cap:k+1,head:0,tail:0,buf:make([]int,k+1),}
}func (this *MyCircularQueue) EnQueue(value int) bool {if this.IsFull(){return false}this.buf[this.tail]=valuethis.tail=(this.tail+1)%this.capreturn true
}func (this *MyCircularQueue) DeQueue() bool {if this.IsEmpty(){return false}this.head=(this.head+1)%this.capreturn true
}func (this *MyCircularQueue) Front() int {if this.IsEmpty() {return -1}return this.buf[this.head]
}func (this *MyCircularQueue) Rear() int {if this.IsEmpty() {return -1}return this.buf[(this.tail-1+this.cap)%this.cap]
}func (this *MyCircularQueue) IsEmpty() bool {return this.head==this.tail
}func (this *MyCircularQueue) IsFull() bool {return (this.tail+1)%this.cap==this.head
}

队列的应用

队列的应用非常广泛，特别是一些具有某些特殊特性的队列，比如刚刚介绍的循环队列、阻塞队列、并发队列。在很多偏底层系统，框架、中间件的开发中，起着关键性的作用。

• 阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说，就是队列为空的时候，从队头取数据会被阻塞直到有数据可取。队列满的时候，插入数据会被阻塞，直到队列中有空闲位置。我们可以使用阻塞队列来实现一个"生产者-消费者"模型。
  基于阻塞队列实现的"生产者-消费者模型"，可以有效协调生产和消费的速度。当"生产者"生产数据的速度过快，"消费者"来不及消费的时候，存储数据的队列很快就满。生产者就会被阻塞直到消费者消费了数据，生产者才会被唤醒继续生产。

• 在多线程情况下，会有多个线程同时操作队列，这个时候就会存在线程安全问题，如何实现一个线程安全的队列？
  线程安全的队列叫做并发队列。最简单直接的方式是在执行"入队"和"出队"操作之前加锁保证线程安全。但是锁的颗粒度比较大导致并发度低，同一时刻允许一个操作要么入队要么出队。实际上，基于数组的循环队列，利用CAS操作，可以实现非常高效的并发队列。这也是循环队列比链式队列更加广泛的原因。

队列在线程池等有限资源池中的应用

队列的知识就介绍完了，现在看看如何解决讲解队列之前提出的那个问题"为了防止线程的数量过多导致频繁的创建销毁和切换，利用线程池提前创建好一些线程。如果此时线程池没有空闲的线程，是拒绝到来的请求还是将其排队。"
一般有以下两种处理策略。

• 第一种是非阻塞的处理方式，直接决绝找不到空闲线程的请求。
• 第二种是阻塞的处理方式。将暂时找不到空闲线程的请求排队，等到有空闲线程的时候，按序取出排队的请求继续处理。那该如何存储这些排队的请求呢？
• 可以类比生活中的排队情景，谁来的早谁先被服务，也就是"先进先出，后进后出"的特性，所以可以使用队列来存储这些排队的请求。
• 队列有两种实现，一种基于链表，一种基于数组。基于链表的实现方式，可以实现一个不限长度的无界队列，但可能对导致排队的请求过多，使得请求的响应时间过长。所以对响应时间要求比较高的系统，不适合使用链表实现的队列。
• 基于数组的实现方式，可以实现一个固定容量的有界队列，排队的请求一旦超过队列的容量就会被丢弃。要根据应用的场景设置一个合适的容量，设置的太大会导致排队的请求过多，设置的太小会导致很多请求被丢弃无法充分利用系统资源。

实际上，对于大部分资源有限的场景，当没有空闲资源时，都可以通过队列这种数据结构实现请求的排队。队列除了应用在线程池中还可以应用在数据库连接池中。

设计循环双端队列

前面我们分析过"循环队列"的实现，为了区分队满和队空的时候头尾指针重合的情况，空出一个位置或者用一个额外的变量记录队列中的元素个数。循环双端队列也一样需要考虑这些，相比与循环队列唯一不同的就是头尾都可以插入和删除元素。
使用size

class MyCircularDeque {
public:MyCircularDeque(int k):cap(k),size(0),head(0),tail() ,buf(new int[k]){}bool insertFront(int value) {if(isFull()) return false;buf[head]=value;head=(head-1+cap)%cap;++size;if(size==1) tail=(tail+1)%cap;return true;}bool insertLast(int value) {if(isFull()) return false;buf[tail]=value;tail=(tail+1)%cap;++size;if(size==1) head=(head-1+cap)%cap;return true;}bool deleteFront() {if(isEmpty()) return false;head=(head+1)%cap;--size;if(size==0) tail=head;return true;}bool deleteLast() {if(isEmpty()) return false;tail=(tail-1+cap)%cap;--size;if(size==0) head=tail;return true;}int getFront() {if(isEmpty()) return -1;return buf[(head+1)%cap];}int getRear() {if(isEmpty()) return -1;return buf[(tail-1+cap)%cap];}bool isEmpty() {return size==0;}bool isFull() {return size==cap;}
private:int cap,size;int head,tail;int *buf;
};

空出一个位置

class MyCircularDeque {
public:MyCircularDeque(int k):cap(k+1),head(0),tail() ,buf(new int[k+1]){}bool insertFront(int value) {if(isFull()) return false;head=(head-1+cap)%cap;buf[head]=value;return true;}bool insertLast(int value) {if(isFull()) return false;buf[tail]=value;tail=(tail+1)%cap;return true;}bool deleteFront() {if(isEmpty()) return false;head=(head+1)%cap;return true;}bool deleteLast() {if(isEmpty()) return false;tail=(tail-1+cap)%cap;return true;}int getFront() {if(isEmpty()) return -1;return buf[head];}int getRear() {if(isEmpty()) return -1;return buf[(tail-1+cap)%cap];}bool isEmpty() {return  head==tail;}bool isFull() {return (tail+1)%cap==head;}
private:int cap;int head,tail;int *buf;
};

type MyCircularDeque struct {cap int head,tail intbuf []int
}func Constructor(k int) MyCircularDeque {return MyCircularDeque{cap:k+1,head:0,tail:0,buf:make([]int,k+1),}
}func (this *MyCircularDeque) InsertFront(value int) bool {if this.IsFull(){return false}this.head=(this.head-1+this.cap)%this.capthis.buf[this.head]=valuereturn true
}func (this *MyCircularDeque) InsertLast(value int) bool {if this.IsFull(){return false}this.buf[this.tail]=valuethis.tail=(this.tail+1)%this.capreturn true
}func (this *MyCircularDeque) DeleteFront() bool {if this.IsEmpty(){return false}this.head=(this.head+1)%this.capreturn true
}func (this *MyCircularDeque) DeleteLast() bool {if this.IsEmpty(){return false}this.tail=(this.tail-1+this.cap)%this.capreturn true
}func (this *MyCircularDeque) GetFront() int {if this.IsEmpty(){return -1}return this.buf[this.head]
}func (this *MyCircularDeque) GetRear() int {if this.IsEmpty(){return -1}return this.buf[(this.tail-1+this.cap)%this.cap]
}func (this *MyCircularDeque) IsEmpty() bool {return this.head==this.tail
}func (this *MyCircularDeque) IsFull() bool {return (this.tail+1)%this.cap==this.head
}

滑动窗口最大值

https://leetcode.cn/problems/sliding-window-maximum/

• 这道题的本质呢就是求固定长度窗口内的最大值。
• 最容易想到的思路就是"暴力双层循环"，外层以窗口长度为步长遍历列表，内层循环寻找固定窗口内的最大值。时间复杂度为O(nk)其中k为固定窗口的长度。
• 由于有些固定窗口的最大值是相同的，我们可以将其保存在一种数据结构中，除了要找到最大值还要判断该最大值是否是当前查找的窗口内的最大值，所以还要保存数值对应的下标。不同窗口的最大值排在一起形成一个队列，队头的元素就是窗口的最大值，若队顶的元素不在当前窗口的范围内将其出队。所以队列除了队尾进，队尾出还要能保证队头出，所以需要使用双端队列[上一题也分析过如何实现]。

typedef pair<int,int> pa;
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {deque<pa> de;//双端队列vector<int> ans(nums.size()-k+1);//存储最终的答案int in=0;for(int i=0;i<nums.size();++i){while(!de.empty()&&nums[i]>de.back().first){de.pop_back();}de.push_back(make_pair(nums[i],i));if(i>=k-1){while(de.front().second<=i-k){de.pop_front();}ans[in++]=de.front().first;}}return ans;}
};

• 由于可以通过下标找到元素数值，所以只存储元素所在下标也可以

func maxSlidingWindow(nums []int, k int) []int {ans:=make([]int,len(nums)-k+1)in:=0de:=make([]int,0,len(nums))for i,_:=range nums{for len(de)!=0 && nums[i]>nums[de[len(de)-1]]{de=de[:len(de)-1]}de=append(de,i)if i>=k-1{for de[0]<=i-k{de=de[1:]}ans[in]=nums[de[0]]in++}}return ans}

讲解完了"队列和栈"，来看看如何用栈实现队列，如何用队列实现栈吧

用栈实现队列

https://leetcode.cn/problems/implement-queue-using-stacks/

• 栈的结构特性是"先进后出"，队列的结构特性是"先进先出"。单用一个栈实现队列是不可能的，所以需要一个辅助栈。也就是用两个栈实现队列。假设现有A\B两个栈，
• 对于Push操作。新的元素直接推进A栈的尾部。
• 对于Pop操作。对于队列来说应该pop最先加入的元素，但是位于栈顶的元素是最后加入的。所以依次对A栈进行pop操作，并将元素加入到B栈，此时B栈栈顶的元素就是最先加入的元素也就是队头元素。
• 对于empty操作。A\B栈都为空，队列才为空。

class MyQueue {
public:MyQueue() {}void push(int x) {a.push(x);}int pop() {int x = peek();b.pop();return x;}int peek() {if(!b.empty()) return b.top();while(!a.empty()) {b.push(a.top());a.pop();}return b.top();}bool empty() {return a.empty()&&b.empty();}
private:stack<int>a;stack<int>b;
};

type MyQueue struct {a,b []int
}func Constructor() MyQueue {return MyQueue{a:[]int{},b:[]int{},}
}func (this *MyQueue) Push(x int)  {this.a=append(this.a,x)
}func (this *MyQueue) Pop() int {x:=this.Peek()this.b=this.b[:len(this.b)-1]return x
}func (this *MyQueue) Peek() int {if len(this.b)!=0 {return this.b[len(this.b)-1]}for i:=len(this.a)-1;i>=0;i--{this.b=append(this.b,this.a[i])}this.a=this.a[:0]return this.b[len(this.b)-1]
}func (this *MyQueue) Empty() bool {return len(this.a)==0 && len(this.b)==0
}

用队列实现栈

https://leetcode.cn/problems/implement-stack-using-queues/description/

用两个队列实现栈的思路

• 现有A、B两个队列。
• 对于Push操作，直接推入A队列的尾部。
• 对于Pop操作，队头的元素是先加入的元素，而对于栈来说pop应该是最后加入的元素。如何保存这个最后加入的元素呢。这时候需要用到辅助队列，每次新加入的元素都是加入到A队列的尾部，为了避免再次加入的元素排到上次加入元素的后面，先将A队列复制给B队列A队列清空，然后再将新元素加入到A队列，之后将B队列的元素重新拿到A队列，这样就可以保证队头的元素永远是最新加入的。
• 这样一来,Pop操作的时间复杂度为O(1)，Push操作的时间复杂度为O(n)
• 对于empty操作，A队列为空则栈为空。

class MyStack {
public:MyStack() {}void push(int x) {while(!a.empty()) {b.push(a.front());a.pop();}a.push(x);while(!b.empty()) {a.push(b.front());b.pop();}}int pop() {int x = a.front();a.pop();return x;}int top() {return a.front();}bool empty() {return a.empty();}
private:queue<int> a;queue<int> b;
};

type MyStack struct {a,b []int
}func Constructor() MyStack {return MyStack{a:[]int{},b:[]int{},}
}func (this *MyStack) Push(x int)  {for i:=0;i<len(this.a);i++{this.b=append(this.b,this.a[i])}this.a=this.a[:0]this.a=append(this.a,x)this.a=append(this.a,this.b ...)this.b=this.b[:0]
}func (this *MyStack) Pop() int {x:=this.a[0]this.a=this.a[1:]return x
}func (this *MyStack) Top() int {return this.a[0]
}func (this *MyStack) Empty() bool {return len(this.a)==0
}

用一个队列实现栈的思路
用两个队列可以实现一个栈，那用一个队列能不能实现栈的功能呢？答案是可以的。队列里保存元素的顺序刚好和栈保存元素的顺序是相反的[队头的元素是最先加入的，队尾的元素是后加入的。栈顶的元素是后加入的，栈尾的元素是最先加入的]，基于此我们可以在将元素入队之后重新出队再入队就可以使队中的元素反转一下，这样队头的元素就是栈顶的元素，队尾的元素就是栈尾的元素。[每次反转之前，可以先记录下当前队内的元素总数，避免将之前反转过的元素重复反转]

class MyStack {
public:MyStack() {}void push(int x) {int size=qu.size();qu.push(x);while(size--){qu.push(pop());}}int pop() {int x = top();qu.pop();return x;}int top() {return qu.front();}bool empty() {return qu.empty();}private:queue<int>qu;
};

type MyStack struct {a []int
}func Constructor() MyStack {return MyStack{a:[]int{},}
}func (this *MyStack) Push(x int)  {size:=len(this.a)this.a=append(this.a,x)for size>0{this.a=append(this.a,this.Pop())size--}
}func (this *MyStack) Pop() int {x:=this.Top()this.a=this.a[1:]return x
}func (this *MyStack) Top() int {return this.a[0]
}func (this *MyStack) Empty() bool {return len(this.a)==0
}