题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

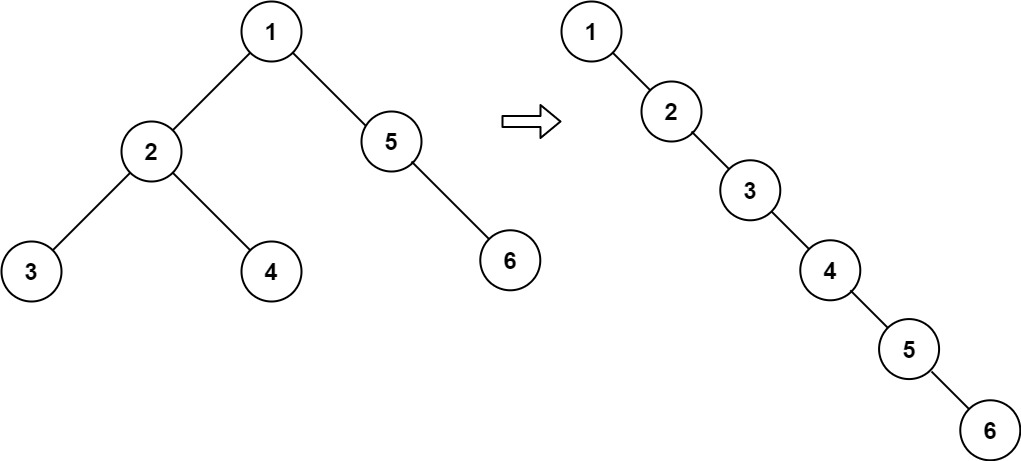
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解法一（常规思路求解）

1. 把root的左右子树拍平
2. 把root的左子树移动到root的右子树
3. 把root的左子树置为null
4. 把root原来的右子树拼接到root原来左子树拍平后的末尾

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public void flatten(TreeNode root) {if (root == null) {return;}// 首先展开左右子树flatten(root.left);flatten(root.right);// 如果左子树为空，当前节点无需处理if (root.left == null) {return;}// 将左子树插入到右子树的位置TreeNode temp = root.right;root.right = root.left;root.left = null; // 将左子节点设为null// 找到现在右子树(原来的左子树)的最末节点TreeNode current = root.right;while (current.right != null) {current = current.right;}// 将原先的右子树接到当前右子树的末端current.right = temp;}
}

后序遍历的重要性：在处理当前节点之前，必须先处理它的左右子树。这是因为展开操作需要修改子树的结构。如果我们先处理当前节点再处理子树，那么当我们返回到当前节点时，子树可能已经被展开并且连接到了当前节点的右侧。这将使得递归调用混乱，并可能导致错误或遗漏某些节点。

解法二（利用pre记录之前的节点）

1. 把root的右左子树拍平
2. 把root的左子树移动到root的右子树
3. 把root的左子树置为null
4. 更新前驱节点pre

class Solution {private TreeNode pre = null;public void flatten(TreeNode root) {if (root == null)return;//注意这个顺序不能对调,否则pre记录的就是右子树就会出错flatten(root.right);flatten(root.left);//由于是后续遍历，pre记录的是左子树的根结点root.right = pre;root.left = null;pre = root;}}

总结

本题要求将二叉树展开为单链表，保持先序遍历顺序。解法一通过递归展开左右子树，然后调整指针顺序；解法二利用pre记录前驱节点，依次处理右子树、左子树，最后更新前驱节点。两种方法均在原地完成，空间复杂度为O(1)。