前几章讨论过的线性规划问题的一个共同特点是:最优解的取值可以是分数或者小数。然而,在许多实际问题中,决策者要求最优解必须是整数,例如公交车的车辆数、员工的人数、机器的台数、产品的件数等。那么,我们能否将得到的非整数最优解“舍入化整”呢?答案是否定的,原因在于(1)非整数最优解化为整数后可能不再是可行解;(2)即使是可行解,也有可能不再是其整数可行解范围内的最优解。因此,我们有必要单独研究那些最优解必须是整数的线性规划问题,即整数线性规划问题。
1958年,R. E. Gomory 在《Outline of an algorithm for integer solutions to linear programs》一文中提出了求解整数规划问题割平面法,此后整数规划作为一个独立的研究分支受到人们的广泛关注。1960年,A. H. Land 和A. G. Doig 在《An automatic method for solving discrete programming problems》中提出了分支定界法(Branch and Bound Method),大幅度提高了整数规划的求解效率。目前,整数规划仍然是运筹学研究的热点,研究者们提出了许多高效的求解方法来解决各种问题,已经在交通运输、物流供应链、生产制造和金融等领域取得了巨大的成功。
通过对整数规划问题基础知识的梳理和总结,小编绘制了《整数规划思维导图》,如下图所示。整数规划问题章节一共有5个知识点和12个子知识点。
第一个知识点是整数规划的数学模型,该部分包括整数规划数学模型的一般形式和数学模型的类型两个子知识点。
第二个知识点是解整数规划的割平面法,该部分主要讲解了两个子知识点,分别是割平面法的基本思路和求解步骤。
第三个知识点是解整数规划的分支定界法,它为整数规划模型的求解提高了效率,该部分将会对分支定界法的核心思想和求解步骤2个子知识点进行具体介绍。
第四个知识点是0-1型整数规划,这部分主要包括0-1型整数规划的定义、应用和隐枚举法3个子知识点。
第五个知识点是指派问题,包括3个子知识点,介绍了指派问题的数学模型和指派问题的独特算法——匈牙利解法,对于非标准形式的指派问题及其求解方式也进行了介绍。
今天,小编先带大家学习整数规划的数学模型和割平面法。
一、整数规划的数学模型
1、一般形式

2、问题分类
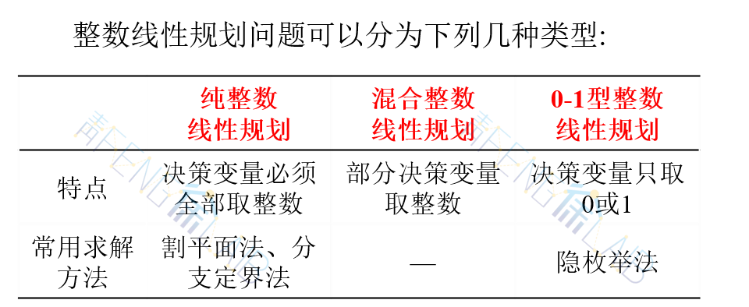
3、例题展示
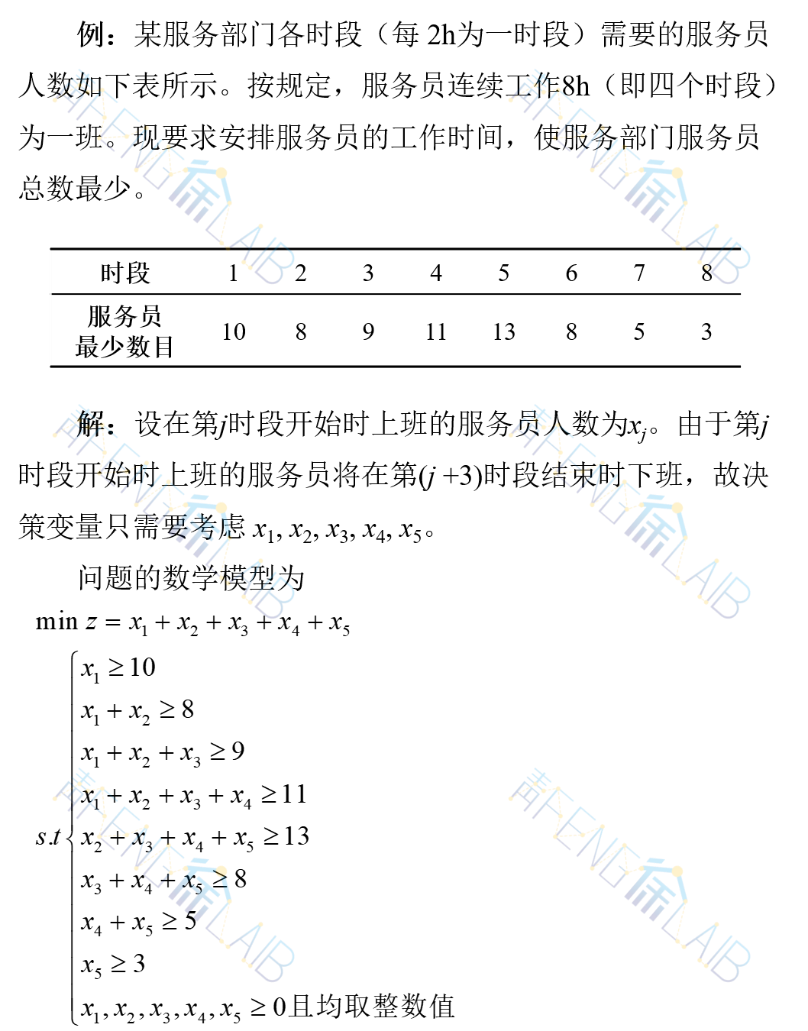
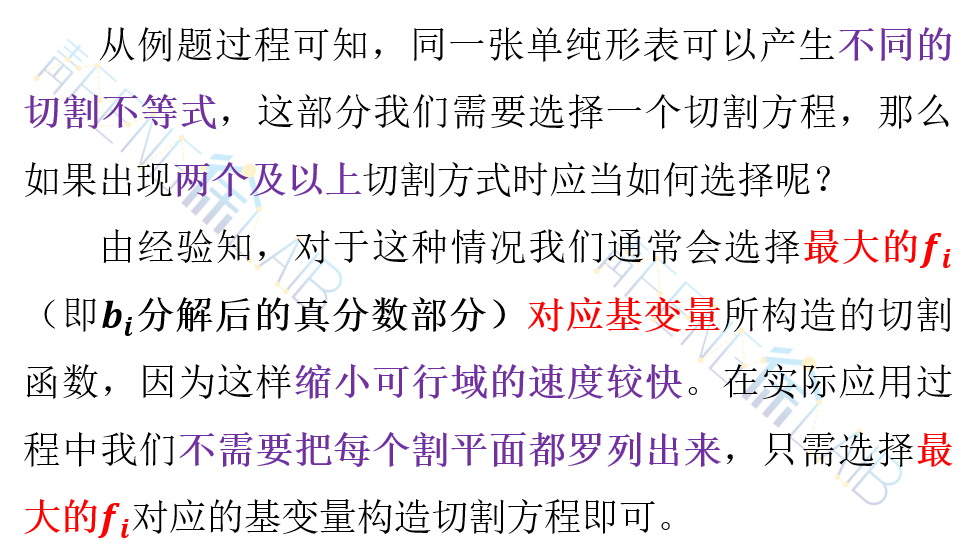
二、割平面法
1、解题思路


2、解题步骤

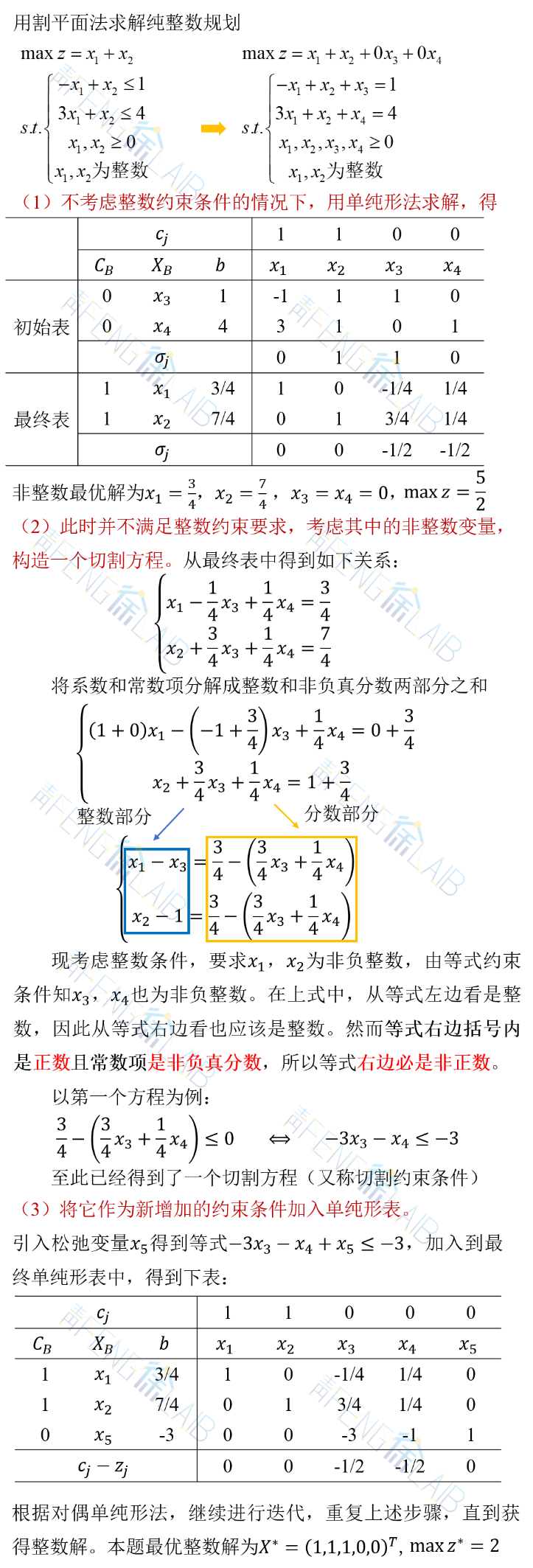
3、例题
4、注意事项