目录
- 假设检验
- 一、假设检验的思想
- 二、假设检验的基本步骤
- 1. 确定要进行检验的假设
- 2. 选择检验统计量。
- 3. 确定用于做决策的拒绝域
- 4. 求出检验统计量的值
- 5. 查看样本结果是否位于拒绝域内
- 6. 做出决策
- 三、举例说明
- 例子1——某公司治疗打鼾
- 例子2——女士品茶的故事
假设检验
一、假设检验的思想
假设检验的基本思想是 “小概率事件”原理 ,其统计推断方法是带有某种概率性质的反证法。小概率思想是指小概率事件在一次试验中基本上不会发生。
反证法思想是先提出检验假设,再用适当的统计方法,利用小概率原理,确定假设是否成立。即为了检验一个假设H0是否正确,首先假定该假设H0正确,然后根据样本对假设H0做出接受或拒绝的决策。如果样本观察值导致了“小概率事件”发生,就应拒绝假设H0,否则应接受假设H0。
“小概率事件”的概率越小,否定原假设H0就越有说服力,常记这个概率值为 α(0<α<1),称为检验的显著性水平。对于不同的问题,检验的显著性水平α不一定相同,一般认为,事件发生的概率小于0.1、0.05或0.01等,即“小概率事件” 。
二、假设检验的基本步骤
1. 确定要进行检验的假设
- 零假又称原假设,符号是H0。
零假设成立时,有关统计量应服从已知的某种概率分布。 - 备择假设的符号是H1 。
预先设定的检验水准为0.05;当检验假设为真,但被错误地拒绝的概率,记作α,通常取α=0.05或α=0.01 。
2. 选择检验统计量。
根据资料的类型和特点,可分别选用Z检验,T检验,秩和检验和卡方检验等 。
3. 确定用于做决策的拒绝域
我们把拒绝域的分界点称为“c”——临界值。定下“显著性水平”后,临界值大小一般可通过查阅相应的界值表得到。
能够拒绝原假设的检验统计量的所有可能取值的集合,称为拒绝域;
在构建拒绝域的时候,还要明白一件事,所构建的是 “单边检验” 还是 “双边检验”
单边检验分为左边和右边
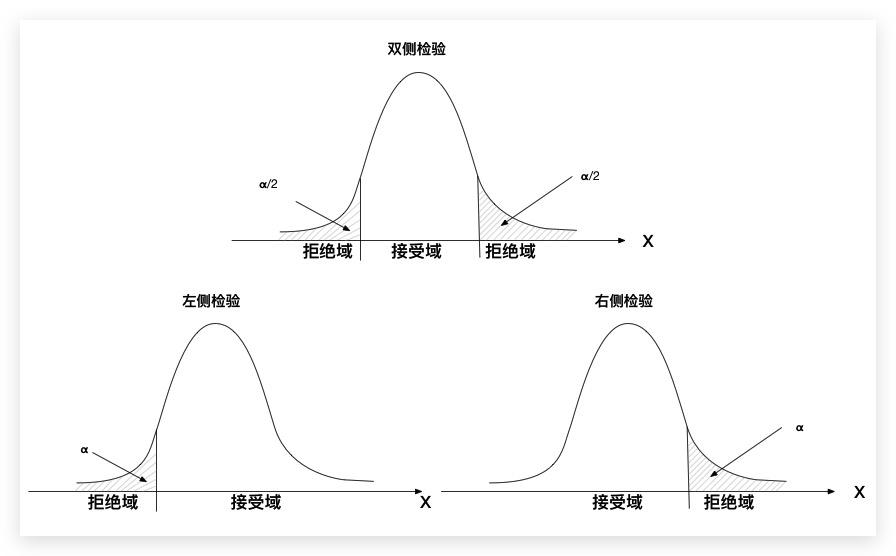
判断依据:
【左边】
如果备选假设包含<符号,则使用左尾,此时拒绝域位于数据的左端
【右边】
如果备选假设包含>符号,则使用右尾,此时拒绝域位于数据的右端
【双边检验】
如果备选假设包含≠符号,则使用双尾检验
即将拒绝域一分为二位于数据两侧,两侧各占α/2,总和为α
不能够拒绝原假设的检验统计量的所有可能取值的集合称为接受域;
根据给定的显著性水平确定的拒绝域的边界值,称为临界值。
4. 求出检验统计量的值
5. 查看样本结果是否位于拒绝域内
统计量与临界值比较。
6. 做出决策
如果统计量不在拒绝域,不拒绝H0;如果统计量在拒绝域,拒绝H0,接受H1。
三、举例说明
例子1——某公司治疗打鼾
某公司声称他们发明了一种治疗打鼾的新药物鼾克,并断言能在两周内治愈90%的患者。随机抽取了15位鼻鼾患者,看他们使用新药物鼾克后是否不再打鼾。结果如下:
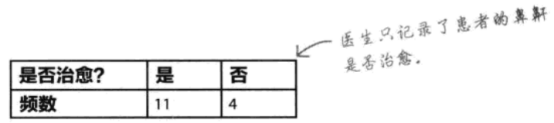
先假设制药公司的断言属实,然后看医生得到的结果是否有误。作出决策:根据证据,接受或否定制药公司的断言。通常以上过程称为假设检验——做出假设或断言,对照证据进行检验。假设检验的一般步骤如下:
第1步:确定假设
我们所检验的这个断言被称为原假设,用H0表示。那么鼾克的这个原假设就是:
H0:p=0.9
那么鼾克的这个备择假设就是:
H1:p<0.9
注:在进行假设检验时,你假定原假设为真,如果有足够的证据反驳原假设,则拒绝原假设,接受备选假设。原假设处于一种被保护的地位。
第2步:选择检验统计量
确定检验内容以后,就需要通过某些手段进行检验,这可以借助检验统计量实现。
我们做假设检验的目的是检验药物的治愈率是否达到90%以上,为此可以根据制药公司的说法查看概率分布,看看抽样中的成功次数是否显著。
如果用X表示样本人数,样本中共有15名患者,成功概率为90%,由于X符合二项式分布,于是检验统计量符合:
X~B(15,0.9)
第3步:确定拒绝域
假设检验的拒绝域是一组数值,这组数值给出反驳原假设的最极端证据。我们把拒绝域的分界点称为——临界值。
那么如何求解拒绝域呢?在求解拒绝域之前我们得确定下显著性水平。若我们想以5%为显著性水平检验制药公司的断言,这说明我么选取的的拒绝域应使得“鼻鼾患者治愈人数小于k”的概率小于0.05,即概率分布最低端的5%部分。
我们对鼾克使用的是单边检验,由于备择假设为p<0.9,因此拒绝域位于左边。
P(X<k)<α
α=5%
第4步:求出检验统计量的值
P(X≤11)=1-P(X≥12)
=1-(P(X=12)+P(X=13)+P(X=14)+P(X=15))
=1-(0.1285+0.2669+0.3432+0.2059)
=1-0.9445 =0.0555
第5步:样本结果是否位于拒绝域内
因为 P(X≤11) =0.0555 >0.05 ,所以P没有落在拒绝域内。
第6步:作出决策
因为假设检验的P值落在检验的拒绝域外,因此没有充分证据可以拒绝原假设H0,原假HO成立,所以我们接收制药公司治愈率为90%的断言。
例子2——女士品茶的故事
1920年的剑桥大学,某个风和日丽的下午,一群科学家正悠闲地享受下午茶时光。正如往常一样准备冲泡奶茶的时候,有位女士突然说:“冲泡的顺序对于奶茶的风味影响很大。先把茶加进牛奶里,与先把牛奶加进茶里,这两种冲泡方式所泡出的奶茶口味截然不同。我可以轻松地辨别出来。”在场的绝大多数人对这位女士的“胡言乱语”嗤之以鼻。然而,其中一位身材矮小、戴着厚眼镜的先生却不这么看,他对这个问题很有兴趣。这个人就是费歇尔(R. A. Fisher)。
他首先假该设女士没有这个能力(这个假设被称为原假设)。随后,Fisher将8杯已经调制好的奶茶随机地放到那位女士的面前,看看这位女士能否正确地品尝出不同的茶。
第1步:确定假设
H0:女士没有这个能力(每次分辨正确的概率P为0.5)
p=0.5
H1:女士有这个能力
p>0.5
第2步:选择检验统计量
用字母p表示该女士每次答对的概率,用随机变量k表示女士答对的次数;在n次实验中,女士答对k次的概率可以用二项分布来描述:

检验统计量符合
X~B(15,0.9)
在原假设下,女士并没有鉴别的能力,能否答对完全靠蒙——此时,p=0.5(类似于抛硬币)。
我们可以计算出 女士答对k次的概率,如下图2所示:
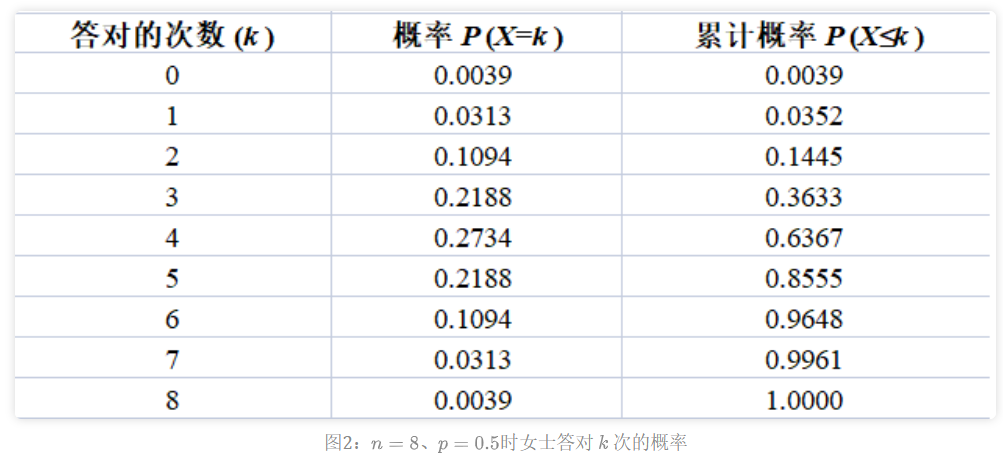
第3步:确定拒绝域
根据备用假设可知是单边检验的右边检验:
P(X>k)<α
α=5%
第4步:求出检验统计量的值
P(x>=8)=0.39%
第5步:样本结果是否位于拒绝域内
P(x>=8)=0.0039<0.05,统计量没有落在拒绝域内。
第6步:作出决策
因为假设检验的统计值P落在检验的拒绝域,当小概率事件发生时,我们有足够的理由怀疑原假设H0的正确性,因而我们拒绝原假设,接受备用假设H1,即女士有这个能力。