77. 组合
题目链接:组合
视频讲解:带你学透回溯算法-组合问题
回溯其实和递归是密不可分的,解决回溯问题标准解法也是根据三部曲来进行的。
1、递归函数的返回值和参数
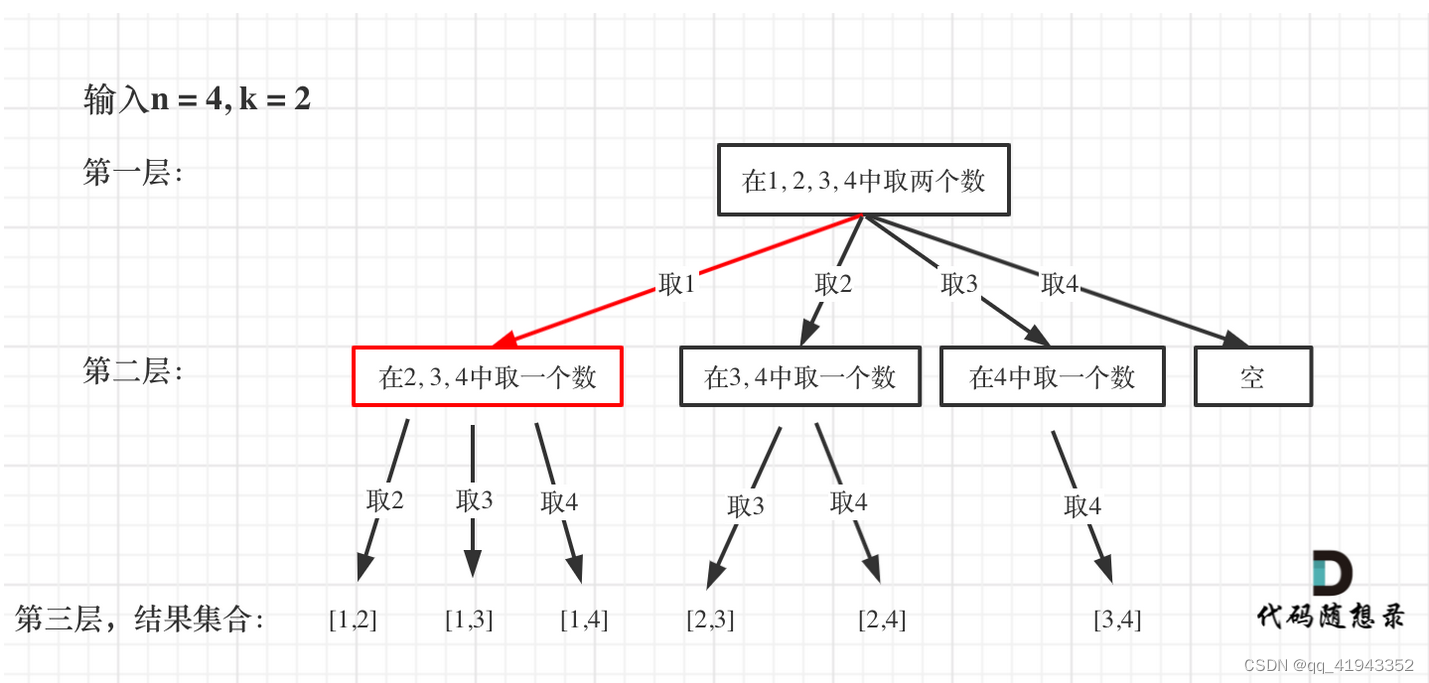
对于本题,我们需要用一个数组保存单个满足条件的组合,还需要另一个结果数组放满足条件组合的集合,可以把他们定义为全局变量,那么递归函数就不需要返回值了。需要传入的参数是集合n和需要取出元素的个数k,当然还需要一个定位的参数startIdx来记录本层递归中,集合从哪里开始遍历。
如果在第二层中取元素,我们就需要用startIdx来定位从哪里开始取了。
2、确定终止条件
当保存单个满足条件的组合的数组元素个数等于k时,本层递归结束,并把这个组合放到结果数组中。
3、确定单层搜索逻辑
回溯法搜索的过程就是一个树形结构的遍历过程,for循环是横向遍历,递归的过程是纵向遍历的。当遍历到所要得的组合,就该回溯,撤销本次处理的结果,向其他处遍历。
// 时间复杂度: O(n * 2^n)
// 空间复杂度: O(n)
class Solution {
private:vector<int> v;vector<vector<int>> ret;void backtracking(int n, int k, int startIdx){if (v.size() == k){ret.push_back(v);return;}for (int i = startIdx; i <= n; ++i){v.push_back(i);backtracking(n, k, i + 1);v.pop_back();}}public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return ret;}
};本题还可以用剪枝优化一下,如:对于n=4,k=4的情况,在第一层for循环的时候从元素2往后的遍历都没有意义了,因为后面没有足够的元素构成有k个元素的组合了。
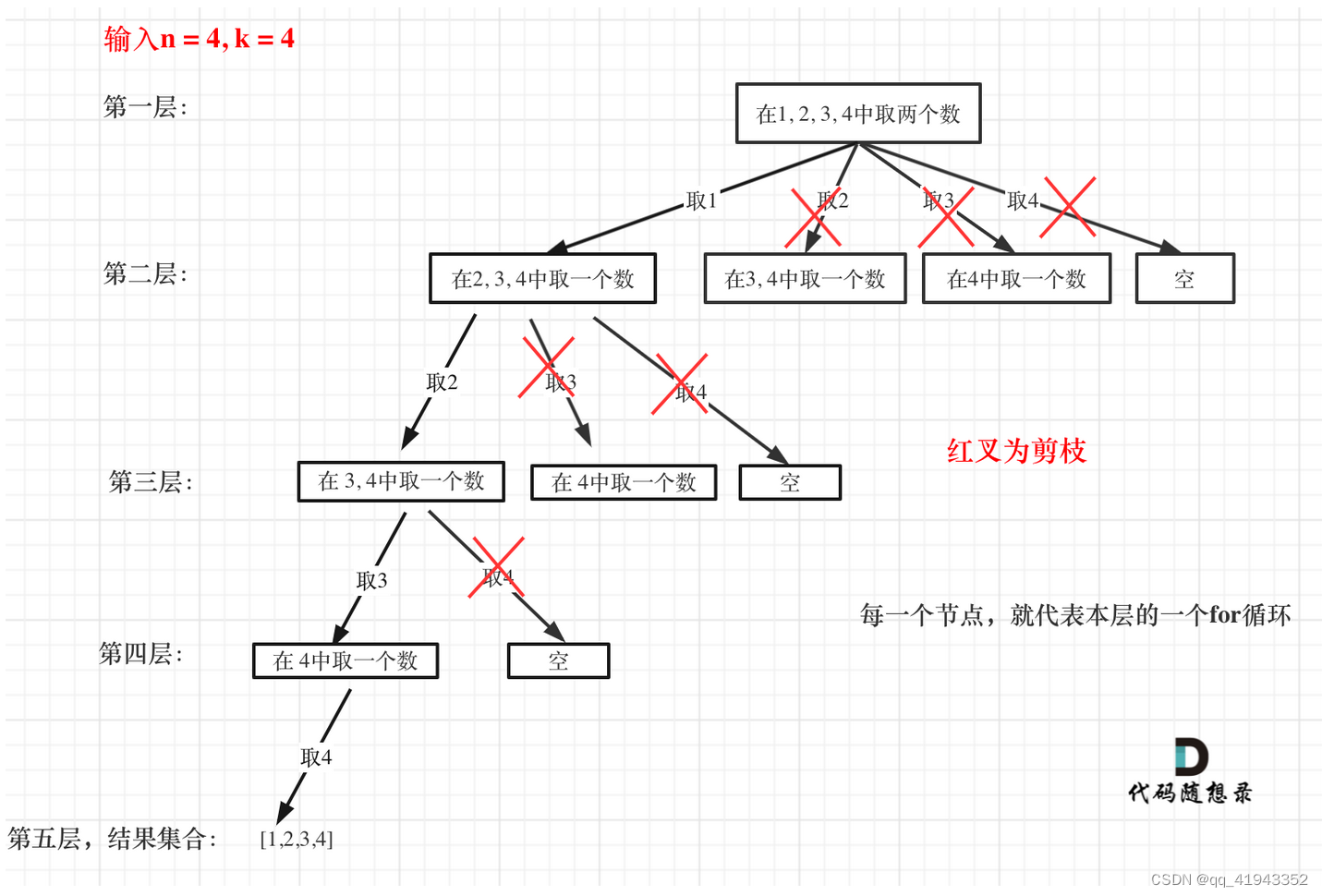
所以我们就要限制for中遍历的起始位置,当这个位置后面元素不足时,就没必要往后搜索了。
class Solution {
private:vector<int> v;vector<vector<int>> ret;void backtracking(int n, int k, int startIdx){if (v.size() == k){ret.push_back(v);return;}for (int i = startIdx; i <= n - (k - v.size()) + 1; ++i){v.push_back(i);backtracking(n, k, i + 1);v.pop_back();}}public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return ret;}
};