总结

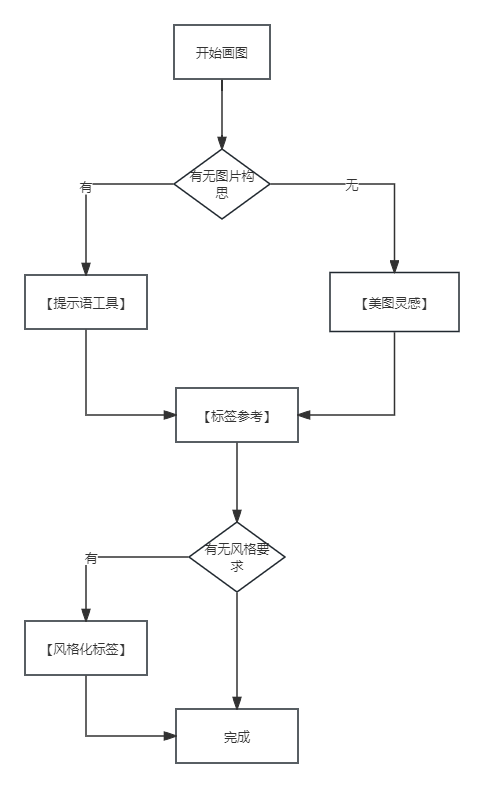
时间安排

$8:00\sim 10:00$ 开 $T1$。第一眼看上去并没有明确的思路，简单想了想发现可以直接贪心走，不过好像有点小细节。推了推细节发现还是用线段树维护写起来顺一点。$9:40$ 写完并调完第一发。不过他题目给的 $n=5\times 10^5$，而我用线段树的频率异常之高，害怕被卡常就测了一发极限数据。一测发现线段树有一点写挂了！给的大样例压根就没测出来……简单一改加个快读就跳了。

$10:00\sim 10:30$ 开 $T2$。一眼看上去感觉 $T2$ 并不难，很快想到了一个莫队计算区间出现数字种类数的做法，但是 $n=5\times 10^5$。总感觉这个问题很典，但是并没想出来怎么做。中间想过主席树，不过也没想出来咋用。于是乎就先把莫队写了，拿个 $60pts$。

$10:30\sim 10:50$ 开 $T3$。看到极差就觉得肯定是个套路题，但是不知道极差有啥套路……开始想二分极差，但是发现搞不了。接着就想二分最大值，然后 $dp$ 出来最小值最大能是多少。不过细想了一下发现二分好像不是很对，好像得三分。凭着感觉写完了三分套 $dp$，调了一小会过了样例就没再管。

$10:50\sim 11:50$ 开 $T4$。$T4$ 也能看出来是套路题（指统计贡献），但是感觉太麻烦了，而且无思路，就开始想暴力。$O(n^3)$ 很好搞，不过并没有这一档部分分！开始想怎么搞 $O(n^2)$。口胡了一个枚举根，在遍历树的时候顺带计算一下答案。感觉很对就写了，写完就发现寄了。很多情况没考虑到。缝缝补补调了一大晌，手玩样例发现这个做法好像就不对……然后就罚坐到了比赛结束。

考试结果

$95+60+100+0=255pts$, $Rank:1$（虽然只有两个人）。$T1$ 线段树终究被卡常了……

考试总结

\qquad 意识到 $T1$ 可能被卡常后就应该再深入剖析一下线段树做的操作是什么。维护 $Sum$ 是单点修改，区间查询，维护 $Day$ 是区间修改单点查询，这两者都可以用常数更小的树状数组来维护。而对于 $Dat$ 完全可以用 $ST$ 表代替。

\qquad $T2$ 确实很典，树状数组就能搞。以前的一些知识、套路还是掌握的不牢固。

题解

T1

\qquad 一个显而易见的性质：如果遇到了一个会让小 $P$ 破产的点 $i$，那么我们一定会在 $1\sim i$ 中收益最大的点积攒经济直到可以通过点 $i$。模拟上述过程即可。可以用树状数组搞到 $O(n\log n)$，也可以直接用一个变量来储存偏移量，因为我们只会用到上一个位置和前缀最值的信息。前缀最值预处理一下即可，整体复杂度就可以降至 $O(n)$。

T2

\qquad 我们显然不能直接枚举 $k$，考虑我们可以怎样给 $k$ 贡献答案。对于一个位置 $i$，如果 $a_i$ 之前没有出现过，那么我们要给所有的 $k$ 贡献 $1$ 的插入次数。如果 $a_i$ 之前出现过，记上一次出现过的位置为 $ls{t}_i$。假设 $(ls{t}_i,i)$ 之间的数字种类数为 $num$，那么我们会对所有 $k\le num$ 的 $k$ 贡献 $1$ 的插入次数。证明显然。这样我们就把问题转化为：一共有 $m$ 个形如 $[ls{t}_i+1,i-1]$ 的区间，对于每一个区间，求出区间内出现过的数字的种类数。假设种类数为 $num$，那么我们让 $s_{num}$ 加一，最后求一个 $s$ 的后缀和就是答案。现在，我们考虑如何快速求一段区间内出现过的数字的种类数。

\qquad 这个问题是不是很熟悉？我们将每个区间挂在区间右端点处，然后从左到右扫区间右端点。对于点 $i$，我们在树状数组上让 $ls{t}_i$ 减一，让 $i$ 加一，对于每一个区间我们求区间和即可。时间复杂度 $O(n\log n)$。

\qquad 核心 $Code:$

for(int i = 1; i <= m; i ++) {if(lst[i]) T.add(lst[i], -1);T.add(i, 1);int Now = T.ask(i);for(auto x : pos[i]) {int ans = T.ask(x - 1);s[Now - ans] ++;}
}

T3

\qquad 直接维护最小极差是不好维护的。二分极差后 $check$ 也是非常难搞的。但是我们注意到，如果知道当前集合中的最大值，那么我们只要尽可能地让最小值最大，就可以最小化极差。所以我们可以考虑二分最大值……吗？

\qquad 直接二分是不行的，因为如果最大值过大，大到序列中任何两个数都拼不出这个最大值，那这个最大值也一定是不优的。所以我们考虑三分最大值。（不过在这想道题的过程中，我突然发现三分也可以求出二分的最优值！好愚蠢地发现啊）最大值固定后，让最小值最大就好搞了，简单 $dp$ 即可。设 $d{p}_{i,0/1/2}$ 表示第 $i$ 个数 \, 未与前面结合，不新开一段/未与前面结合，新开一段/与前面结合，新开一段 \, 能得到的最小值。转移很好转。

\qquad 核心 $Code:$

int check(int x) {memset(dp, 0x7f, sizeof dp);for(int i = 1; i <= n; i ++) {if(a[i] + a[i - 1] <= x) dp[i][2] = min(dp[i - 1][0], a[i] + a[i - 1]);//能与前面结合if(dp[i - 1][2] != 0x7f7f7f7f) dp[i][1] = min(max(dp[i - 1][1], dp[i - 1][2]), a[i]);//新开一段else dp[i][1] = min(dp[i - 1][1], a[i]);if(dp[i - 1][2] != 0x7f7f7f7f) dp[i][0] = max(dp[i - 1][1], dp[i - 1][2]);//不新开一段else dp[i][0] = dp[i - 1][1];}//由于dp[n][0]并没有将n归到某一段内，所以是一个不合法的状态if(dp[n][2] == 0x7f7f7f7f) return x - dp[n][1];return x - max(dp[n][1], dp[n][2]);
}

T4

\qquad 还不会……