评价类问题

解决评价类问题首先需要想到一下三个问题

1. 我们评价的目标是什么
2. 我们为了达到这个目标有哪几种可行方案
3. 评价的准则或者说指标是什么

对于以上三个问题，我们可以根据题目中的背景材料，常识以及网上收集到的参考资料进行结合，从而筛选出最合适的指标
优先选择知网，或者万方，百度学术等平台
有理可依
虫部落-快搜：https://search.chongbuluo.com

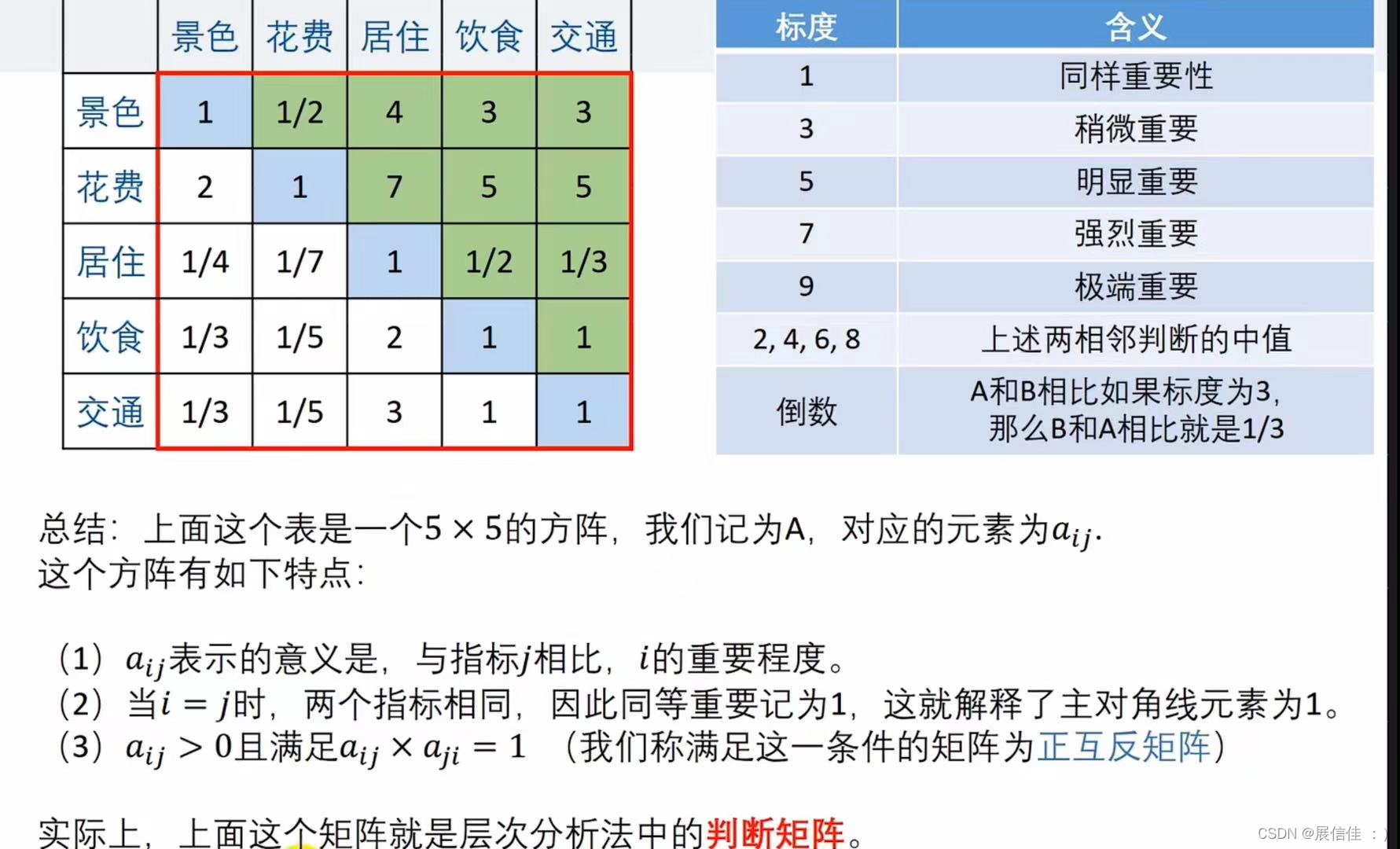
假如你打算去出门游玩，那么可能会考虑景色，花费，居住，饮食，交通五个方面，如果一次性考虑这五个指标之间的关系，往往考虑不周。

我们可以采取分而治之的思想，两个两个指标进行比较，最终根据两两比较的结果来推算出权重

判断矩阵

判断矩阵

一致矩阵

若矩阵中每个元素aij>0,且满足aij X aji=1，则我们称该矩阵为正互反矩阵。
在层次分析法中，我们构造的判断矩阵均为正互反矩阵。

若正互反矩阵满足 aij X ajk = aik ,则我们称其为一致矩阵。 一致矩阵的特点在于每行每列呈倍数关系

一致性检验

注意：在使用判断矩阵求权值之间，必须对其进行一致性检验

n阶正互反矩阵A为一致矩阵时当且仅当最大特征值 r=n
当正互反矩阵A非一致时，一定满足r > n

判断矩阵越不一致时，最大特征值与n相差就越大

权重的计算

1. 一致矩阵
   根据一列的数值做归一化处理
2. 判断矩阵
   按照列做归一化处理后，再求平均值

层次分析法

步骤

1. 分析系统中各因素之间的关系，建立系统的递阶层次结构

2. 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）

3. 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验

权重计算方法有三种：

• 算术平均法
• 几何平均法
• 特征值法

如 CR>0.1 那就尽量往一致矩阵靠拢

建议在比赛时都使用：避免采用单一方法所产生的偏差，得出的结论更全面

局限性

评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异很大