Key Concept
主成分分析(PCA,Principal Component Analysis)是一种统计方法,它通过线性变换将多维数据变换到新的坐标系统中,使得这一数据的任何投影的第一大方差出现在第一个坐标(即第一个主成分)上,第二大方差出现在第二个坐标上,依次类推。
建模思路
-
数据准备与标准化:
- 收集多维数据集,并对其进行标准化处理,通常是减去均值,除以标准差,以保证每个特征维度对结果的贡献是可比的。这里借用了这里的数据来使用PCA进行主成分分析alifrmf/Country-Profiling-Using-PCA-and-Clustering: Unsupervised Machine Learning Analysis Using Clustering Model (github.com)
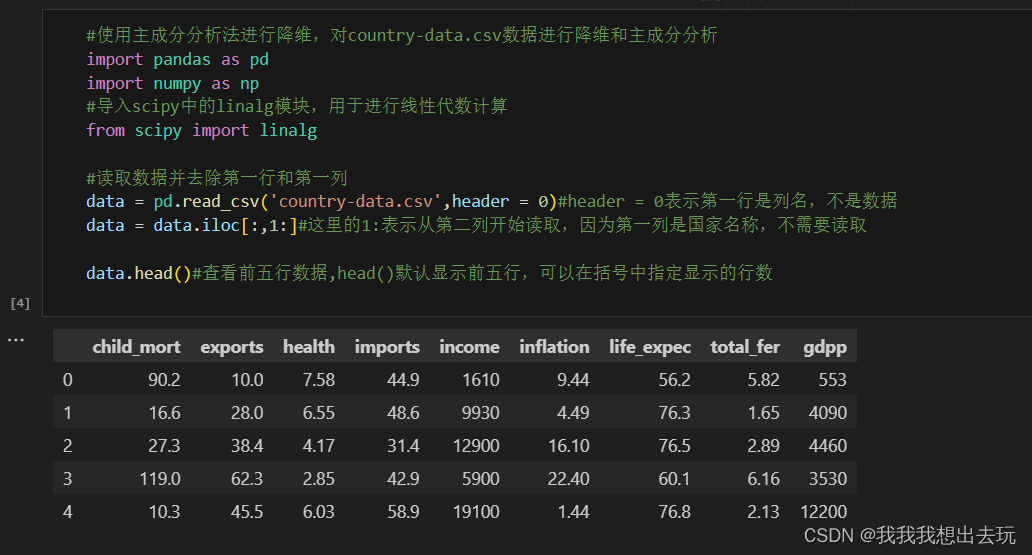
- 将读取的数据转化为numpy数组(矩阵)并进行标准化,使数据落入N(0,1)区间
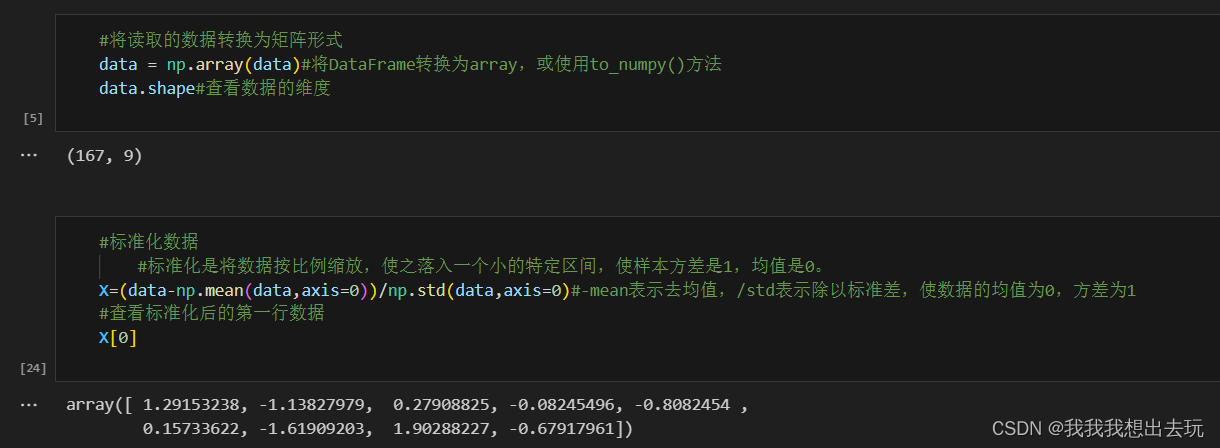
- 收集多维数据集,并对其进行标准化处理,通常是减去均值,除以标准差,以保证每个特征维度对结果的贡献是可比的。这里借用了这里的数据来使用PCA进行主成分分析alifrmf/Country-Profiling-Using-PCA-and-Clustering: Unsupervised Machine Learning Analysis Using Clustering Model (github.com)
-
计算协方差矩阵:
- 计算标准化数据的协方差矩阵。协方差矩阵反映了数据各维度之间的相关性。因为我们读取的数据矩阵中,每行都表示一个国家,每列表示的是不同的特征。PCA要分析的是不同特征之间的相关性,所以我们要把这个矩阵转置之后再求协方差矩阵。

- 计算标准化数据的协方差矩阵。协方差矩阵反映了数据各维度之间的相关性。因为我们读取的数据矩阵中,每行都表示一个国家,每列表示的是不同的特征。PCA要分析的是不同特征之间的相关性,所以我们要把这个矩阵转置之后再求协方差矩阵。
-
求解特征值和特征向量:
- 对协方差矩阵进行特征分解,求出其特征值和相应的特征向量。这里没有像之前层次分析法一样使用numpy的特征值分解方法,而是使用了scipy中的linalg来进行特征值计算
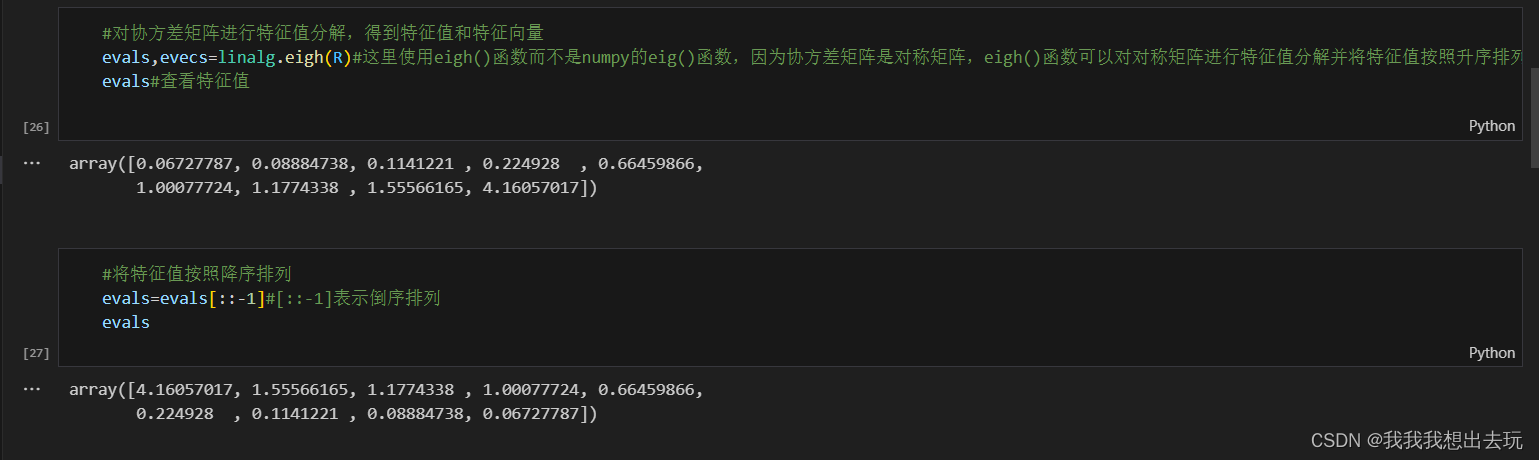
- 对协方差矩阵进行特征分解,求出其特征值和相应的特征向量。这里没有像之前层次分析法一样使用numpy的特征值分解方法,而是使用了scipy中的linalg来进行特征值计算
-
选择主成分:
- 将特征值从大到小排列
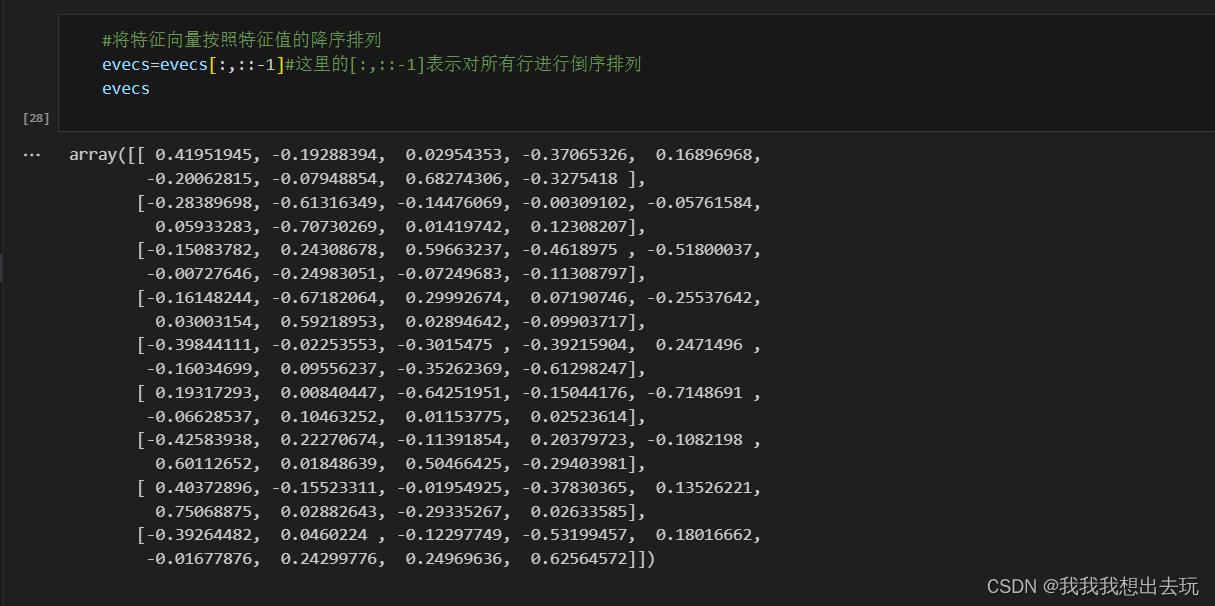
- 计算特征向量的方差累积贡献率。如果前n个特征向量的方差贡献率达到了85%(或者其他界限),则可以选择使用这前n个特征向量作为我们的主成分


- 将特征值从大到小排列
-
主成分分析

PCA还可以进一步用于聚类分析等操作,比如人脸识别这种.......
Key Concept Explanation PCA的核心思想是找到最能代表原始数据集的低维结构,通常用于数据预处理、数据压缩和特征提取。在许多实际应用中,数据集可能包含许多变量,而其中一些变量可能是相关的。PCA使我们能够识别出最重要的变量,即主成分,并且通过这些主成分来简化我们的数据集,同时保留数据集中的大部分信息。
PCA的优势在于它可以用较少的变量解释大部分数据的变异性,有助于去除噪声和冗余特征,同时可以在数据的可视化方面发挥重要作用。然而,PCA也有其局限性,比如它依赖于线性假设,对于非线性关系的数据可能无法有效地提取特征。此外,PCA对异常值非常敏感,可能会影响最终的降维结果。