JavaScript中的浮点数运算有时候会出现一点偏差。下面解释为什么0.1 + 0.2 ≠ 0.3,以及如果你需要精确运算应该怎么做。
如果1 + 2 = 3,那么为什么在JavaScript中0.1 + 0.2 ≠ 0.3?这个原因与计算机科学和浮点数运算有关。
我建议你打开浏览器的控制台,输入0.1 + 0.2来查看结果。

不,你不需要调整浏览器–这就是它应该的工作方式,根据定义JavaScript语言的ECMAScript标准:
“Number类型正好有18437736874454810627(即 2^64 - 2^53 + 3)个值,表示双精度64位格式IEEE 754标准中规定的值”——ECMAScript语言规范
JavaScript使用number基本类型表示数值,所有JavaScript数字实际上都是浮点数 —— 即使是整数。
这里的关键是JavaScript实现了IEEE浮点算术标准。让我们看看这意味着什么。
这里发生了什么?
“你的语言没有出错,它在做浮点运算。计算机只能本地存储整数,所以它们需要某种方法来表示十进制数。这种表示法不是完全准确的。这就是为什么‘0.1 + 0.2 != 0.3’的情况经常发生。” —— Erik Wiffin 在 0.30000000000000004.com
你可能已经知道所有数字在计算机中都是二进制的。
在二进制中,值以2进制的形式表示为0和1的序列,而不是我们通常使用的10进制。
我们得到浮点舍入误差的原因令人着迷,这与循环小数的概念有关。
只有当分母是基数的质因数时,分数才能“整洁地”(意思是作为没有循环小数的精确值)存储。
10进制的质因数是2和5,所以1/2、1/4、1/5、1/8和1/10可以整洁地表达,但是1/3、1/6、1/7和1/9是循环小数。
2进制的惟一质因数是2,所以只有1/2可以整洁地表示 —— 任何其他值都成为循环小数。
这意味着当我们使用0.1这样的10进制小数(1/10)时,它可以用一个十进制数字表示,但在二进制中却不行。
可以在二进制中整洁地表达的唯一分数是0.5(1/2)。可以自己尝试使用 IEEE-754浮点转换器。
浮点数也更慢
JavaScript中的浮点数与整数相比,通常情况下的表现也不同。例如,它们在for循环中更慢。
我们用jsPerf来测试两个微性能案例:

在jsPerf.com上查看这些测试案例
虽然差异不大,但浮点运算的平均速度确实比只使用整数值的基本for循环稍微慢一点。
这发生的原因是上一节中解释的那些二进制中浮点数的额外复杂性。
当然,代码库中这个差异还不足以造成影响,但是这是JavaScript的一个有趣的特性。
如果需要精确计算该怎么办?
如果你需要精确的JavaScript计算,例如处理金融交易,那么最好使用整数。
虽然所有的JavaScript数字在内部都表示为浮点值,但是在处理整数值时,你不会遇到不精确的问题,至少在低于 MAX_SAFE_INTEGER(2^53 - 1)的范围内:

一个方法是只以分工作——例如,通过将19.99美元的值表示为整数1999来代表。
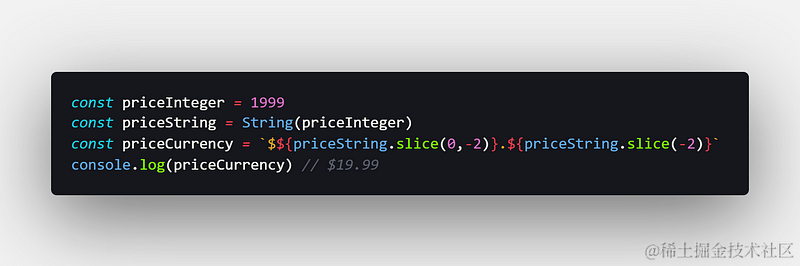
在GitHub Gist上查看原始代码
另一种方法是创建一个对象来表示货币,并在内部使用整数值。例如:
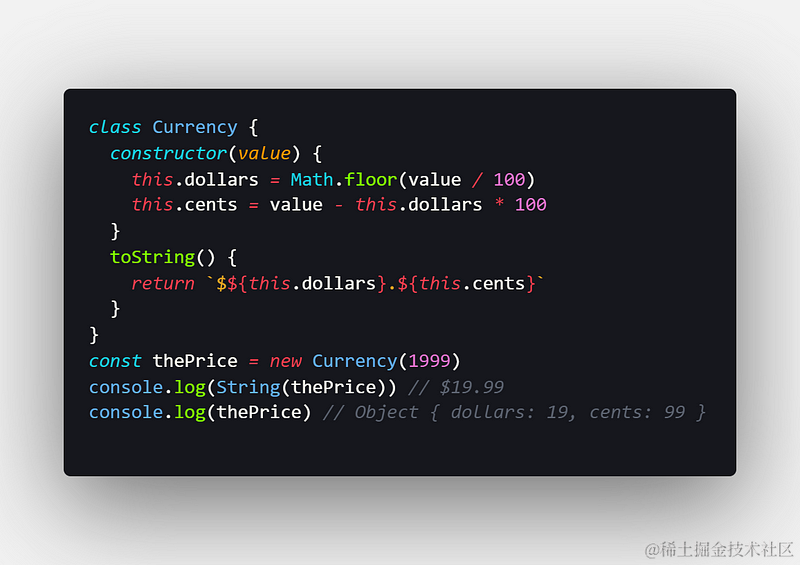
在GitHub Gist上查看原始代码
许多库已经以更强大的方式解决了这个问题,包括accounting.js、currency.js、money.js和Numeral.js。
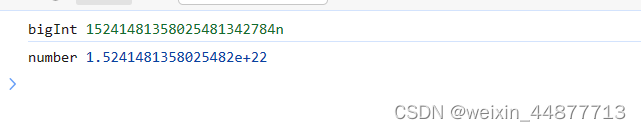
最后,你可以考虑使用BigInt基本类型,它可以表示任意大的整数(但不能表示浮点值):
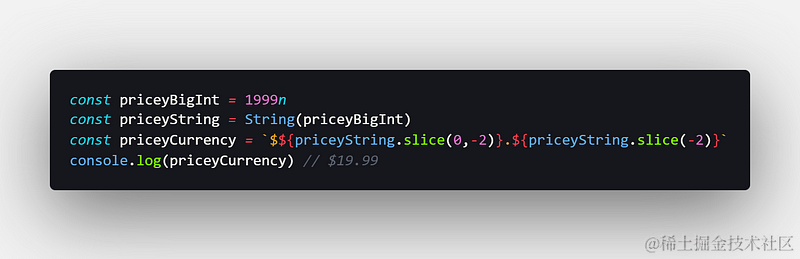
在GitHub Gist上查看原始代码
TypeScript也支持BigInt,所以在TypeScript中使用BigInt可能是一个避免意外使用浮点数据的好选择。
结论
我对0.1 + 0.2实际上应该等于0.30000000000000004感到非常惊讶,因为浮点数运算。
这看起来像一个等待发生的错误,但是没有明确的解决方法,因为ECMAScript规范要求0.1 + 0.2 ≠ 0.3。
幸运的是,整数运算避免了讨厌的舍入误差,所以通过使用JavaScript数字(如果坚持整数)可以实现精确计算。
对于任意精度或确保永远不会有十进制值,你可以考虑使用JavaScript更新的BigInt基本类型。
你也可能会发现exact-math或math.js库很有帮助。它们都是用于使用JavaScript执行精确计算的。
编码快乐!📏🖥️📐⌨️😄