最小生成树（java版）-编程知识

最小生成树（java版）

📑前言

本文主要是【最小生成树】——最小生成树使用的文章，如果有什么需要改进的地方还请大佬指出⛺️

🎬作者简介：大家好，我是听风与他🥇
☁️博客首页：CSDN主页听风与他
🌄每日一句：狠狠沉淀，顶峰相见

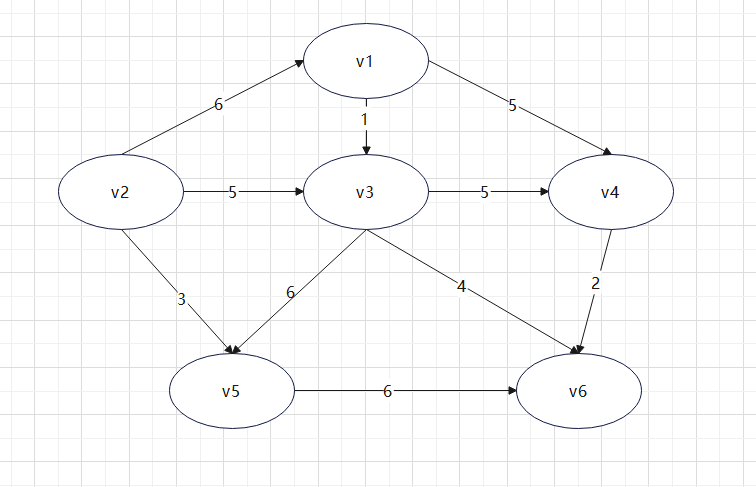
Prime最小生成树

按结点来进行遍历

package 图论;import java.util.Arrays;
import java.util.Scanner;public class 最小生成树_Prime {
/*
6
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0*/public static void main(String[] args) {// TODO Auto-generated method stubScanner sc = new Scanner(System.in);int n = sc.nextInt();//顶点个数int g[][] = new int[n][n];//dis[i]=0; 表示顶点i已经被纳入最小生成树，dis[i]表示最小生成树到顶点i的目前最小距离int dis[] = new int[n];//目前最小生成树到其它未访问顶点的最小距离for(int i=0;i<n;i++) {for(int j=0;j<n;j++) {int w = sc.nextInt();//读入矩阵if(i==j) g[i][j]=0;//自己到自己距离是0else if(w==0) g[i][j]=Integer.MAX_VALUE;//不可达，默认无穷大else {g[i][j]=w;//否则存储真实的权值}}}for(int x[]:g) {System.out.println(Arrays.toString(x));}//prime求最小生成树primedo(g, dis, n);}public static void primedo(int[][] g,int[] dis,int n) {//最小生成树要包含n个结点，所以这里默认开始Vo结点僵尸最小生成树的第一个结点//dis数组存最小生成树到其它未被选择的最小距离0到其它结点的距离for(int i=0;i<n;i++) dis[i]=g[0][i];dis[0]=0;int ans=0;for(int i=1;i<n;i++) {//n个结点，最后选择n-1条边，循环就n-1次int min=Integer.MAX_VALUE;int minindex=-1;//存储最小结点的编号for(int j=0;j<n;j++) {if(dis[j]<min && dis[j]!=0) {min = dis[j];minindex=j;//当前j是最小的，未被纳入的顶点编号}}ans=ans+dis[minindex];dis[minindex]=0;//把dis[minindex]=0表示minindex结点本轮被纳入最小生成树了for(int j=0;j<n;j++) {dis[j]=Math.min(dis[j], g[minindex][j]);}}System.out.println(ans);}
}

Kruskal最小生成树

按边来寻找

package 图论;import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;public class Kruskal {
/*
6 10
0 1 6
0 2 1
0 3 5
1 2 5
1 4 3
2 3 5
2 4 6
2 5 4
3 5 2
4 5 6*/static int[] f;//父亲数组public static int find(int x) {if(f[x]==x) return x;else {f[x]=find(f[x]);return f[x];}}public static boolean merge(int a,int b) {int f1=find(a);int f2=find(b);if(f1!=f2) {f[f1]=f2;return true;//两个顶点来自不同的联通分量}else return false;//否则形成环，这条边是不合法的}public static void main(String[] args) {// TODO Auto-generated method stubScanner sc = new Scanner(System.in);int n = sc.nextInt();int m = sc.nextInt();//n个顶点，m条边int num=0;//表示目前已经采用多少条边int sum=0;//最小生成树的边权累加和f = new int[n];for(int i=0;i<f.length;i++) f[i]=i;//大家属于鼓励联通分量ArrayList<edge> list = new ArrayList<edge>();for(int i=0;i<m;i++) list.add(new edge(sc.nextInt(), sc.nextInt(), sc.nextInt()));Collections.sort(list);for(int i=0;i<list.size();i++) System.out.println(list.get(i));for(int i=0;i<list.size();i++) {//去检测m条边，不断做合并edge check = list.get(i);if (merge(check.start,check.end)) {//根据并查集不断的查找两个顶点是否在同一个集合System.out.println("采纳"+check);sum=sum+check.weight;num++;if(num==n-1) break;}else {System.out.println("不采纳");}}System.out.println(sum);}static class edge implements Comparable<edge>{int start;int end;int weight;public edge(int s,int e,int w) {this.start=s;this.end = e;this.weight=w;}@Overridepublic int compareTo(edge o) {// TODO Auto-generated method stubreturn this.weight-o.weight;}public String toString() {return String.format("start=%d\t end=%d\t weight=%d", start,end,weight);}}
}