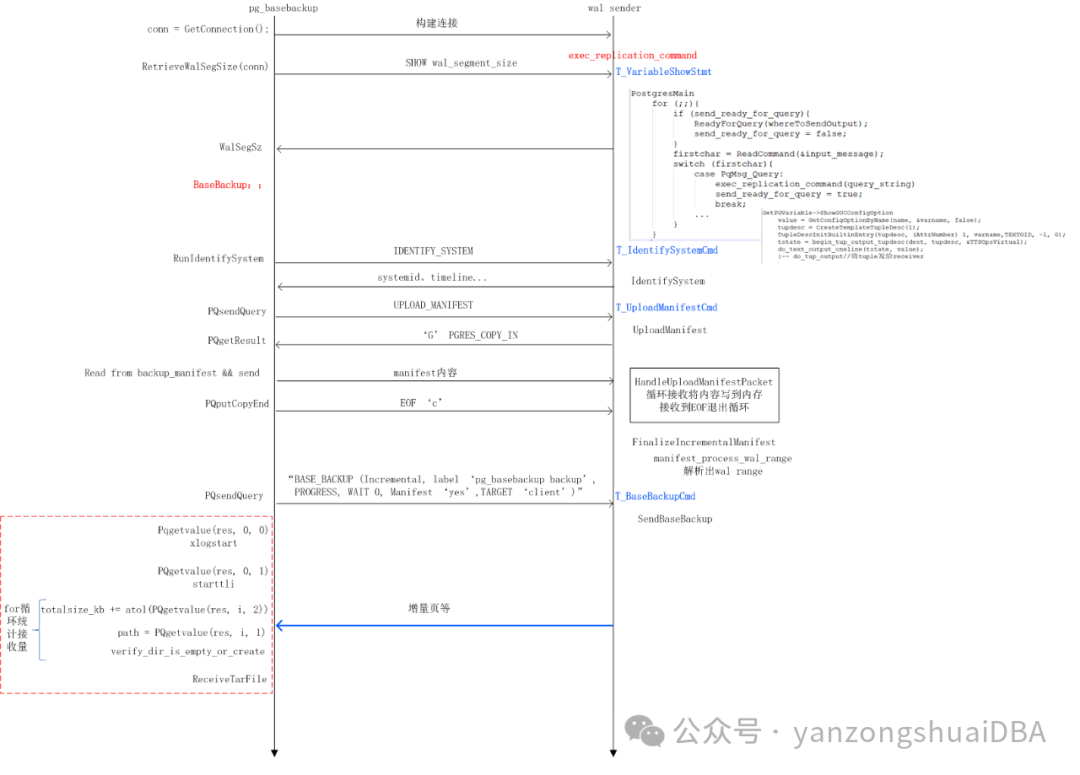
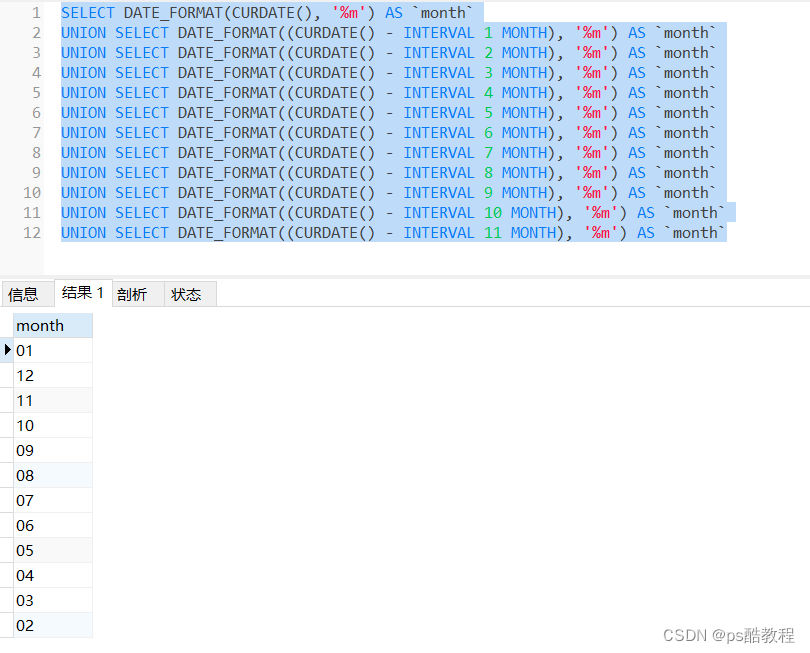
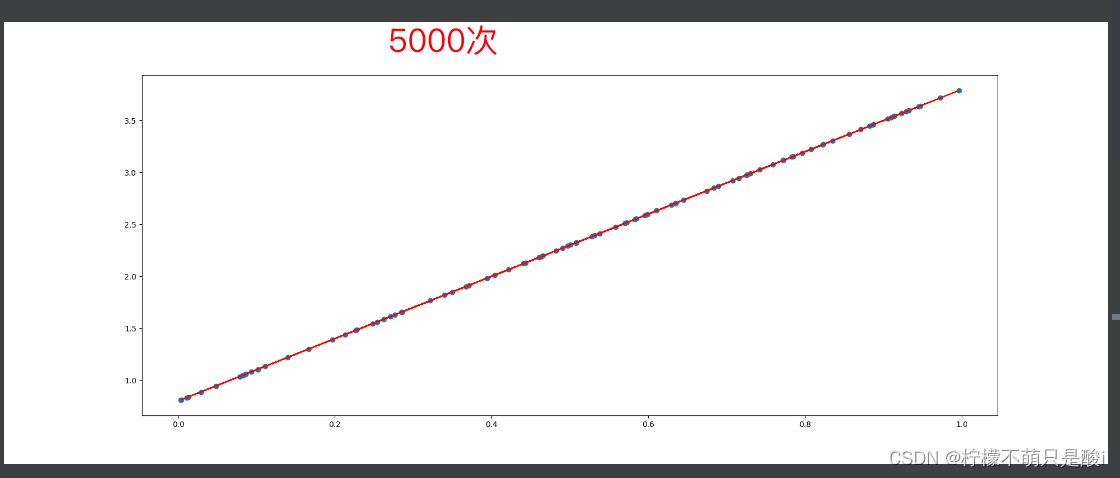
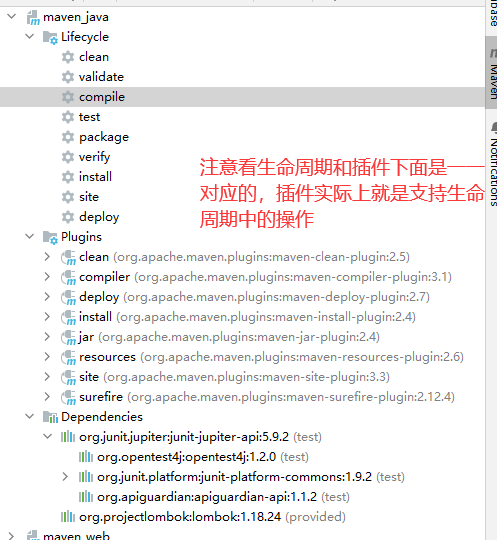
在了解机械臂正解推导的过程中，几个问题一直困扰着我：

1、为什么3*3矩阵可以描述姿态？矩阵更进一步的意义是什么？姿态是否有其他的描述方式，如果有是什么？

2、机械臂法兰中心相对于基座的坐标，6个矩阵连乘的进一步意义？

翻阅过一些材料，《机器人学导论》、《机器人学》(战强)、《机器人学》(蔡自兴，谢斌)，并未解惑。于是自己搜索一些材料，尝试学习。

该从何说起呢？

1、向量空间

1.1向量空间

设V是非空的n维向量的集合(n=1, 2,  3,...)，如果V中的向量对加法和数乘两种运算封闭，即

若a,b∈V，则a+b∈V；

a∈V，则ka∈V，k为任意实数，

则V称为向量空间。

1.2 基、坐标的几何意义

对于向量空间V中一个有序向量组{a₁, a₂, a₃, ... a_n}，若满足：

a₁, a₂, ... a_n线性无关；

V中任意一个向量a都可由a₁, a₂, a₃, ... a_n线性表示，即a = x₁a₁ + x₂a₂ + ... +x_na_n,则称向量组{a₁, a₂, a₃, ... a_n}为向量空间V的一个基；称有序数组{x₁, x₂, ... x_n}为向量a在基{a₁, a₂, a₃, ... a_n}上的坐标，即坐标是相对基而言的。

1.3向量内积

在线性空间如何定义两个向量的长度和夹角？

a . b = ab cosθ

a^T . b = a_xb_x + a_yb_y + a_zb_z

1.4标准正交基

便于计算向量到子空间的投影(坐标)。

三维空间R3标准正交基，右手系标准正交基数学表达式(球坐标系定义式)(r, , φ)：

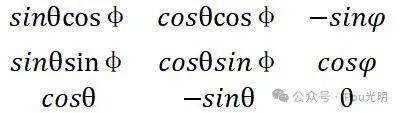
0 <=θ <= π， 0 <=φ<= 2π

与直角坐标系转换：

x=rsinθcosφ.

y=rsinθsinφ.

z=rcosθ.

《线性代数的几何意义》

欢迎大家关注：