01背包的优化
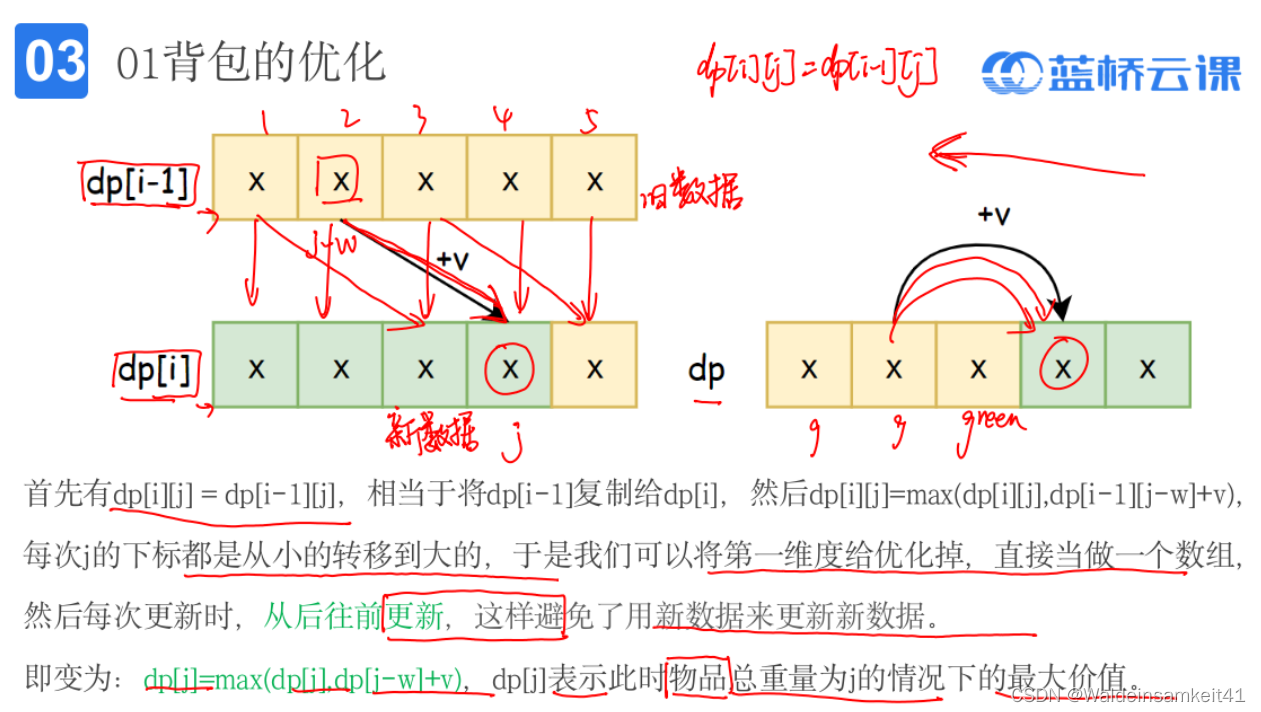
因为我们更新数据时,都是从左到右进行更新的,所以我们可以把二维的dp变成一维的dp,并从后往前进行更新(这样可以保证进行更新的数据都是由旧数据更新新数据,而不是由新数据更新旧数据)
多重背包

朴素的想法就是把s个物品重复一遍,这样就是O(n*m*s),容易超时,所以想想,怎么优化。

有点像倍增的思想,用1 2 4...等等数字,是因为二进制数可以表示任何数字,如果最后有剩余,就把那个剩余单独一组。
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long longll dp[20005];int main()
{int n,m;cin >> n >> m;for(int i = 1 ; i <= n ; i++){ll w,v,s;cin >> w >> v >> s;//s = 14for(int k=1 ; k <= s ; s-=k,k+=k ){//k = 1 2 4 ...for(int j = m ; j >= k*w ; j--){dp[j]=max(dp[j],dp[j-k*w]+k*v);}}//s 还有一部分剩余for(int j = m ; j >= s*w ; j--){dp[j]=max(dp[j],dp[j-s*w]+s*v);}}cout << dp[m];return 0;
}
s-=k,k+=k 保证了每次k是1 2 4...然后s是剩余的、还没有进行相加的数字,如果不满足下一个2的倍数,就自成一组。
单调队列优化多重背包
把时间复杂度降到O(n*m)


就是在 (不放物品、只放1个、放2个、......、放s个)这里面挑个最大值。
第一维可滚掉的意思是:可以把这个数组从后到前进行遍历,来个n次(第次的n都是一个新的物品)。


解释,毕竟这个物品,体积是v,在分完组之后,能对它进行影响的只有 j-v 那个点的值了。

代码。。。找了好多地方的,终于找到一个靠谱的且我能理解的。
以下是通过蓝桥题目的代码。
#include <iostream>
#include <queue>
#include <utility>
#include <algorithm>
using namespace std;
#define ll long longconst int N = 2e4+5;
pair<int,int> q[N];
ll dp[N];
int head,tail;int main()
{int n,V;cin >> n >> V;for(int i = 1 ; i <= n ; i++){int v,w,s;cin >> v >> w >> s;int num = min(V/v,s);for(int mo = 0 ; mo < v ; mo++){head=0,tail=0;for(int k = 0 ; k <= (V-mo)/v ; k++){int y=dp[k*v+mo]-k*w;int x=k;while(head<tail && q[head].first<k-num) head++;while(head<tail && q[tail-1].second<=y) tail--;q[tail++]={x,y};dp[k*v+mo]=q[head].second + k*w;}}}cout << dp[V];return 0;
}费用背包模型

只是多一个维度,代码如下:
int main()
{// 请在此输入您的代码int n,V,M;cin >> n >> V >> M;for(int i = 1 ; i <= n ; i++){int v,m,w;cin >> v >> m >> w;for(int j = V ; j >= v ; j--){for(int k = M ; k >= m ; k--){dp[j][k]=max(dp[j][k],dp[j-v][k-m]+w);}}}cout << dp[V][M];return 0;
}分组背包

每组只能挑一个,可以不挑。
对dp[i][j] 会有 s 次的更新,因为要和同组内进行竞争,所以找dp[i][j]的max会和当时dp[i][j]的值进行对比,为了不漏 dp[i-1][j] ,所以要在组内循环前把 dp[i][j]=dp[i-1][j] 方便之后对比。
int main()
{// 请在此输入您的代码int n,V;cin >> n >> V;for(int i = 1 ; i <= n ; i++){for(int j = 1 ; j <= V ; j++){dp[i][j]=dp[i-1][j];}int s;cin >> s;while(s--){int w,v;cin >> w >> v;for(int j = w ; j <= V ; j++){dp[i][j]=max(dp[i][j],dp[i-1][j-w]+v);}}}cout << dp[n][V];return 0;
}