目录
关于堆的一些知识的回顾
数据结构:堆的特点
"down" 和 "up":维护堆的性质
down
up
数据结构:堆的主要操作
acwing-838堆排序
代码如下
时间复杂度分析
确实是在写的过程中频繁回顾了很多关于树的知识,有关的文章都在专栏里,需要的可以去回顾一下~
http://t.csdnimg.cn/0d6Iq![]() http://t.csdnimg.cn/0d6Iq
http://t.csdnimg.cn/0d6Iq
关于堆的一些知识的回顾
关于堆,我的印象中是内存机制里的堆。之前写过的,在回顾一下吧~

然而我们这里说的堆,其实是一种用数据结构中的完全二叉树实现的堆。
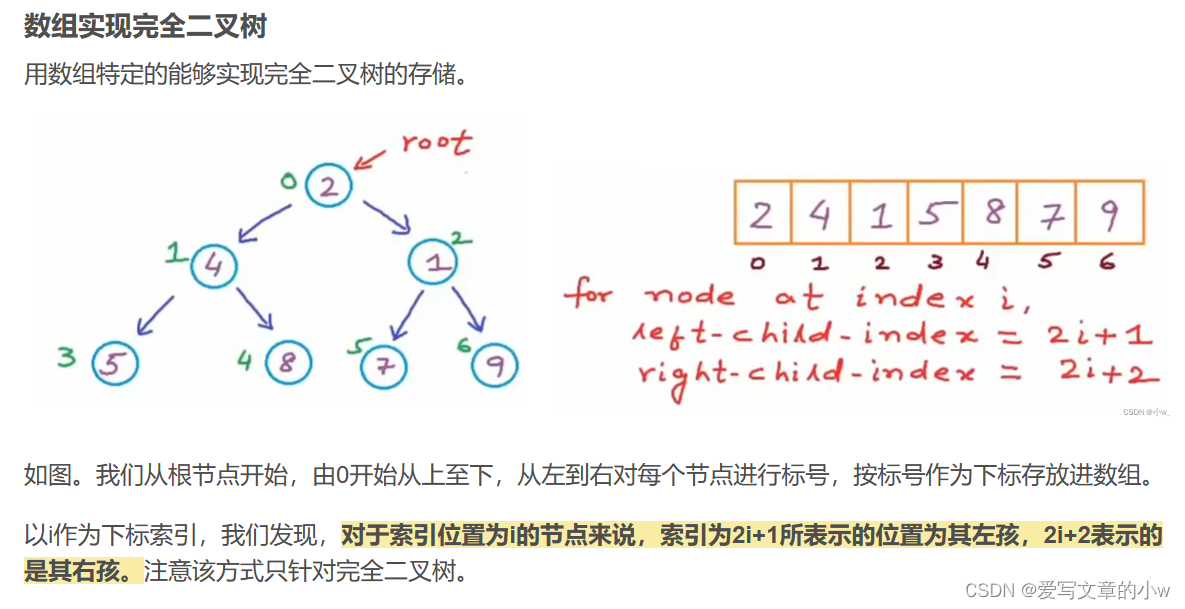
(我们这里图片上写的坐标索引方式是根节点从0开始索引,我们下面会采用下标从1开始索引,那样的话,左儿子就应该是2x 右儿子是2x+1 可以理解哈)
其实这里还要回顾一下树的广度优先遍历,即一层一层,从左到右的遍历方式,对于完全二叉树来说,其广度优先遍历就是创建一个数组,按照特定的存储方式进行存储,最终直接输出数组元素。对于其他的树,采取队列的存储方式。下面这篇文章详细介绍了树的遍历,也对数组存储有更深的解释,感兴趣可以看一下
http://t.csdnimg.cn/NngZ6
数据结构:堆的特点
1.完全二叉树的结构
堆是一个完全二叉树,这意味着除了最底层,其他层都是满的,而最底层的节点都集中在左侧。
到这里就要疑惑为什么堆是完全二叉树这种结构了
http://www.zhihu.com/question/36134980/answer/87490177
这篇文章作者详细解释了关于"堆"这种数据结构好处包括用途,我感觉写的非常不错,可以看一下加深理解。
其中主要提到:1.完全二叉树这种结构可以使用数组实现存储,并且便于索引。
2.它的出现是为了解决----对一个动态的序列进行排序,并且随时想知道这个序列的最小值或最大值
2.最小堆和最大堆
堆可以分为最小堆和最大堆两种类型。在最小堆中,每个节点的值都小于或等于其子节点的值。而在最大堆中,每个节点的值都大于或等于其子节点的值。(也叫小根堆和大根堆)
"down" 和 "up":维护堆的性质
"down" 操作通常涉及到将元素向下移动,适用于删除操作和堆化过程中。
通过 down(k) 进行下沉操作是为了调整以 k 为根的子树,确保其满足最小堆的性质。这主要关注了 k 节点向下的关系。
"up" 操作涉及到将元素向上移动,适用于插入操作和堆化过程中。
通过 up(k) 进行上浮操作是为了确保从删除元素的位置 k 开始,向上到根节点的路径上的每个父节点都满足最小堆的性质。这主要关注了 k 节点向上的关系。
而我们所说的 "down" 和 "up" 是通常用于--维护堆的性质。以确保堆的性质不被破坏。
下面以小根堆为例
down

根据这个思路我们写出代码
//调整以x为根的子树,以满足小根堆的性质(x是经过某种操作得到的值,在操作之前整棵树是满足堆的性质的)
void down(int x)
{int t=x;//t表示三个数中的最小值
//比较的前提都是孩子存在if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t)//所以这里如果不需要交换位置,那说明更改的这个值并没有破坏原有的性质{swap(he[x],he[t]);down(t);//需要交换 说明我们又更改了一个位置的值,所以要继续判断这次更改的是否符合性质}
}down操作的前提就是 本身这个树的每个节点都是符合性质的,只是某一个值发生了改变,
我们针对这个发生改变的值,不管它是插入还是修改还是更改而导致的值的变化,我们最主要的就是关注改值之后,以其为根节点的子树。
将该值与它的原本的左右两个孩子的值的比较,如果不需要交换位置,说明这次的更改的值并没有引起堆的性质的变化
up
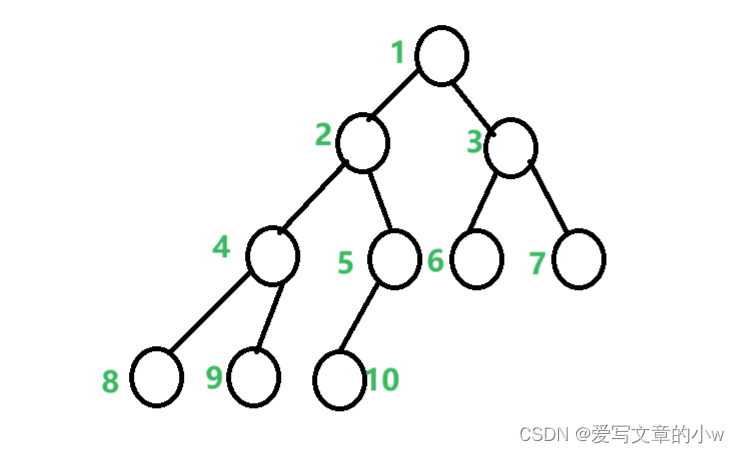
如上图这种完全二叉树,按照数组存储方式,观察其下标表示,我们发现孩子节点是其父节点下标的二倍。
由于小根堆的性质,根节点小于左右孩子,所以我们检查的时候只看该节点与根节点的大小关系就好了,因为另一个孩子一定是大于根节点且符合性质的。
void up(int x)
{while(x/2 && he[x/2]>he[x])//当该元素存在父节点且满足大小关系{swap(he[x/2],he[x]);x /= 2;//更新父节点}
}有了上面down的详细解释这个应该很容易理解了。
数据结构:堆的主要操作
1.插入一个元素,并仍保持堆的性质。
2.删除最小/大值。
3.堆化:将一个无序数组转换为堆,或者修复一个破坏了堆性质的堆。
这里先详细说一下堆化
for(int i=n/2;i;i--)down(i);我们通常从倒数第二层(n/2是最后一个元素的父节点)开始进行逐个元素下沉,最终达到将数组堆化的结果。 这是因为底层节点是叶子节点,它们自身已经满足堆的性质,不需要进行下沉操作。
 关于手写堆的一些主要操作就是上面这些。
关于手写堆的一些主要操作就是上面这些。
下面我逐个来解释。
1.插入一个数。由于我们堆结构是用数组实现存储的完全二叉树,因此对于数组来说,在末尾添加一个元素是很容易的,所以我们先把这个要插入的元素放到堆的末尾,在进行up操作,使其符合堆的性质。
2.求最小值,我们小根堆的根节点就是其最小值。
3.删除最小值。由于我们总是要删除一个元素的,在数组存储结构中,删除最后一个元素是很简单的,直接使我们使用到的下标--就行,但是我们要删的是第一个元素呀,怎么办呢?我们把最后一个元素的值标记覆盖到第一个元素的位置,再删除掉最后一个元素,再把刚刚放到第一位的元素进行down操作,使其符合堆的性质。
4.删除任意一个元素。在3思路的基础上,由于我们不清楚最后一个元素相较于原来这个位置上删除掉的元素是大还是小,如果是大于原来的元素,那就会执行down,如果小于,就会向上执行up,因此,这两个只会执行其中一个,为了简化代码,我们直接不判断,把两个都放上去。
5.修改任意一个元素,解释同4
acwing-838堆排序
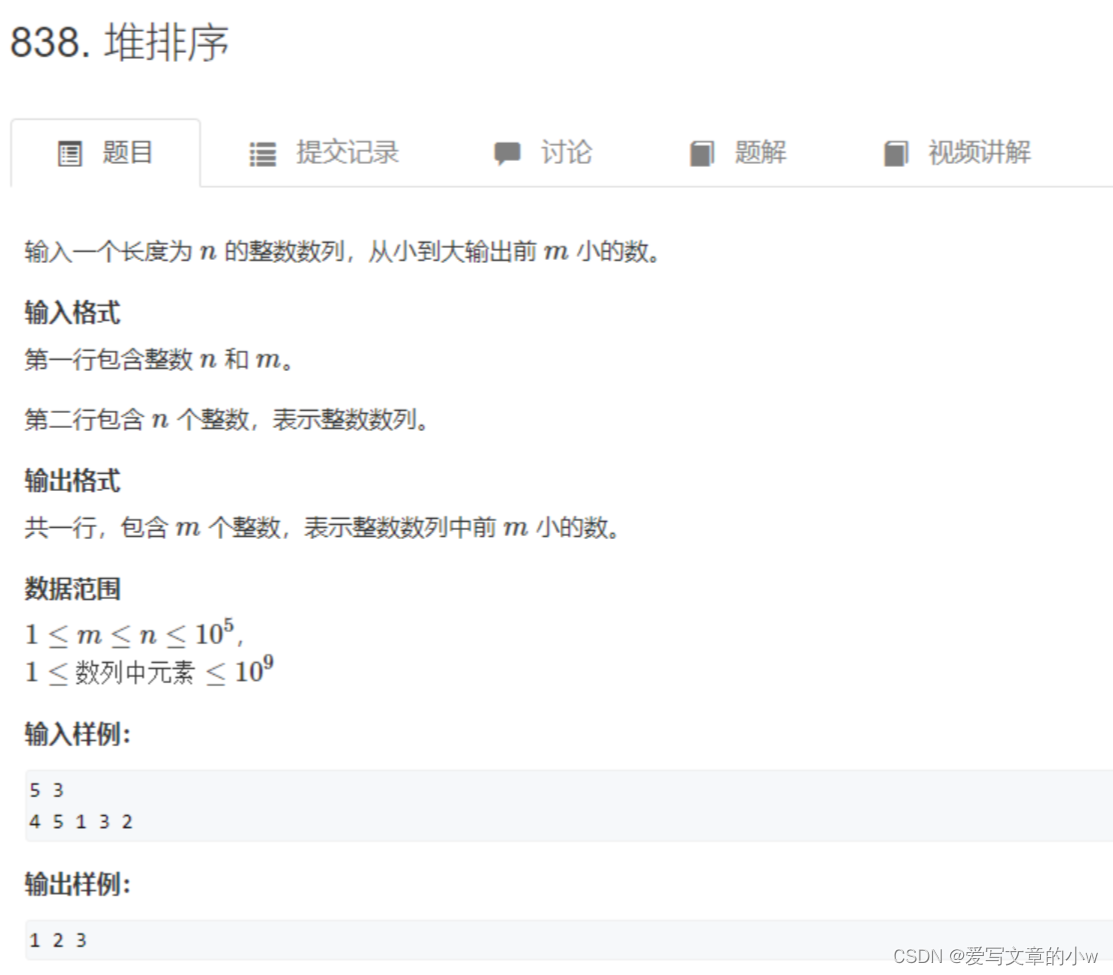
经过上面的介绍其实这道题的核心都已经解了,直接看代码把。
代码如下
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int n,m;
int he[N],size;//调整以 x 为根的子树,以满足小根堆的性质
void down(int x)
{int t=x;//t表示三个数中的最小值if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t){swap(he[x],he[t]);down(t);}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&he[i]);}size=n;//size标记数组最后一个元素for(int i=n/2;i;i--)down(i);//将数组堆化while(m--)//每次输出一个最小值{printf("%d ",he[1]);he[1]=he[size];//删除最小值size--;down(1);}return 0;
}时间复杂度分析
在这段代码中:
①输入数据的for循环O(n)
②建堆的for循环,先看down函数,down是逐层比较,其时间复杂度取决于树的高度,所以最坏情况下就是该二叉树为满二叉树时的树高,即log(n)。那么真整个建堆过程时间复杂度应为O(n*log(n))
--关于这里的时间复杂度其实还有一种思考方式,等之后回来补写一下。
③输出最小值的while循环,也是取决于down函数执行次数,即O(m*log(n))
哎,就差一个模拟堆(烦躁),是有点强迫症在的😢明天在写啦。。
有问题欢迎指出!一起加油!!