矩阵的秩

概念

矩阵的秩是线性代数中的一个重要概念，用于描述矩阵的行（或列）向量的线性无关程度。矩阵的秩可以通过多种方法来确定，其中最常用的是高斯消元法或奇异值分解（SVD）。

对于一个m×n的矩阵，其秩的定义是矩阵中线性无关的行（或列）向量的最大个数。换句话说，秩是指矩阵中非零行（或列）向量的最大线性无关组的大小。

k阶子式

在mxn矩阵A中，任取k行k列（1≤k≤min{m,n}），位于这些行列交叉处的k^2^个元素，

按照它们在A中所处的位置所构成的k阶行列式叫做矩阵A的一个k阶子式。

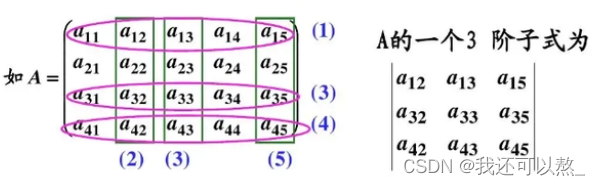
注意

行列式是由一些数值排列成的数表按一定的法则计算得到的一个数
行列式的行数和列数是相等的
mxn矩阵A的k阶子式共有C~m~^k^C~n~^k^个

矩阵的秩的定义

如果在矩阵A中有一个r阶子式D的值不等于零，而所有r+1阶子式（如果存在的话）的

值都等于零，则称数r为矩阵A的秩，记作R(A)。规定零矩阵的秩为0。

矩阵的秩的性质

R(A)=R(A^T^)一个矩阵的行秩和列秩相等，因此通常只谈论矩阵的秩而不区分行秩和列秩。
R(A~mxn~) ≤ min(m,n)任意一个矩阵的秩不会超过其行数或列数（较小的那个）。
如果一个矩阵的秩等于其行数或列数（较小的那个），则该矩阵被称为满秩矩阵。对于n阶方阵A，若|A|≠ 0，有R(A)=n，则称A为满秩矩阵；若|A|= 0，则R(A)<n，则称A为降秩矩阵。满秩矩阵是可逆矩阵，降秩矩阵是不可逆矩阵。

SVD分解

概念

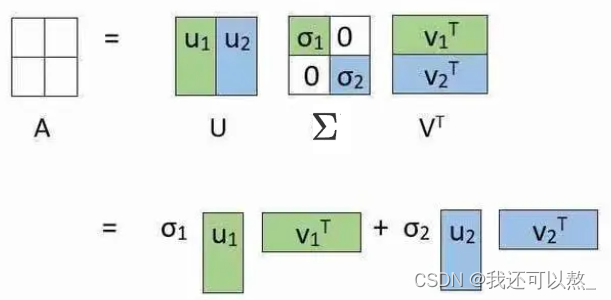
奇异值分解（Singular Value Decomposition，简称SVD）是一种常用的矩阵分解方法，可以将一个矩阵分解为三个矩阵的乘积：A = UΣV^T，其中 A 是一个 m×n 的矩阵，U 是一个 m×m 的正交矩阵，Σ 是一个 m×n 的对角矩阵，V^T 是一个 n×n 的正交矩阵，^T 表示转置。

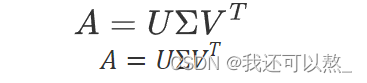
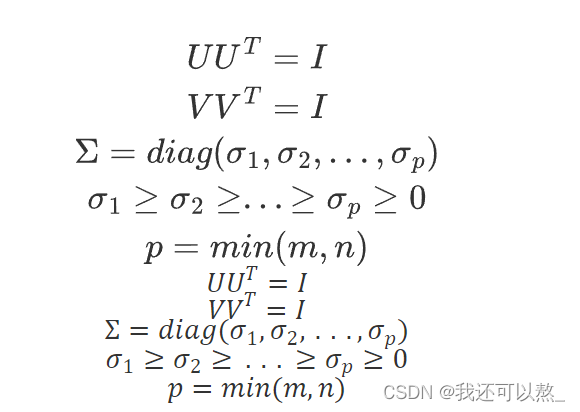
σ~i~称为矩阵A的奇异值，U的列向量称为左奇异向量；V的列向量称为右奇异向量

注意

特征值分解只能针对于方阵而言，而奇异值分解可以应用于任意形状矩阵

SVD的分解过程

对矩阵 A 的转置矩阵 A^T 乘以 A，得到一个对称矩阵 B = A^T·A。
对对称矩阵 B 进行特征值分解，得到特征值和特征向量。设特征值为 λ1, λ2, ..., λr，特征向量为 v1, v2, ..., vr（其中 r 是矩阵 A 的秩）。
将特征向量 v1, v2, ..., vr 归一化，得到单位向量 u1, u2, ..., ur。
构建矩阵 U = [u1, u2, ..., ur]，即将归一化后的特征向量按列排列成矩阵。
计算矩阵 V 中的列向量。对每个特征值 λi，计算 Bv_i = λi v_i，然后将 v_i 归一化得到单位向量 w_i。构建矩阵 V = [w1, w2, ..., wr]。
构建对角矩阵 Σ = diag(√λ1, √λ2, ..., √λr)，即将特征值开方后按顺序排列成对角矩阵。

通过这样的分解，矩阵 A 可以表示为 UΣV^T 的形式，其中 U、Σ 和 V^T 分别代表了 A 的左奇异向量、奇异值和右奇异向量。