https://leetcode.cn/problems/container-with-most-water/solutions/207215/sheng-zui-duo-shui-de-rong-qi-by-leetcode-solution/?envType=study-plan-v2&envId=top-100-liked

 

         1、暴力求解

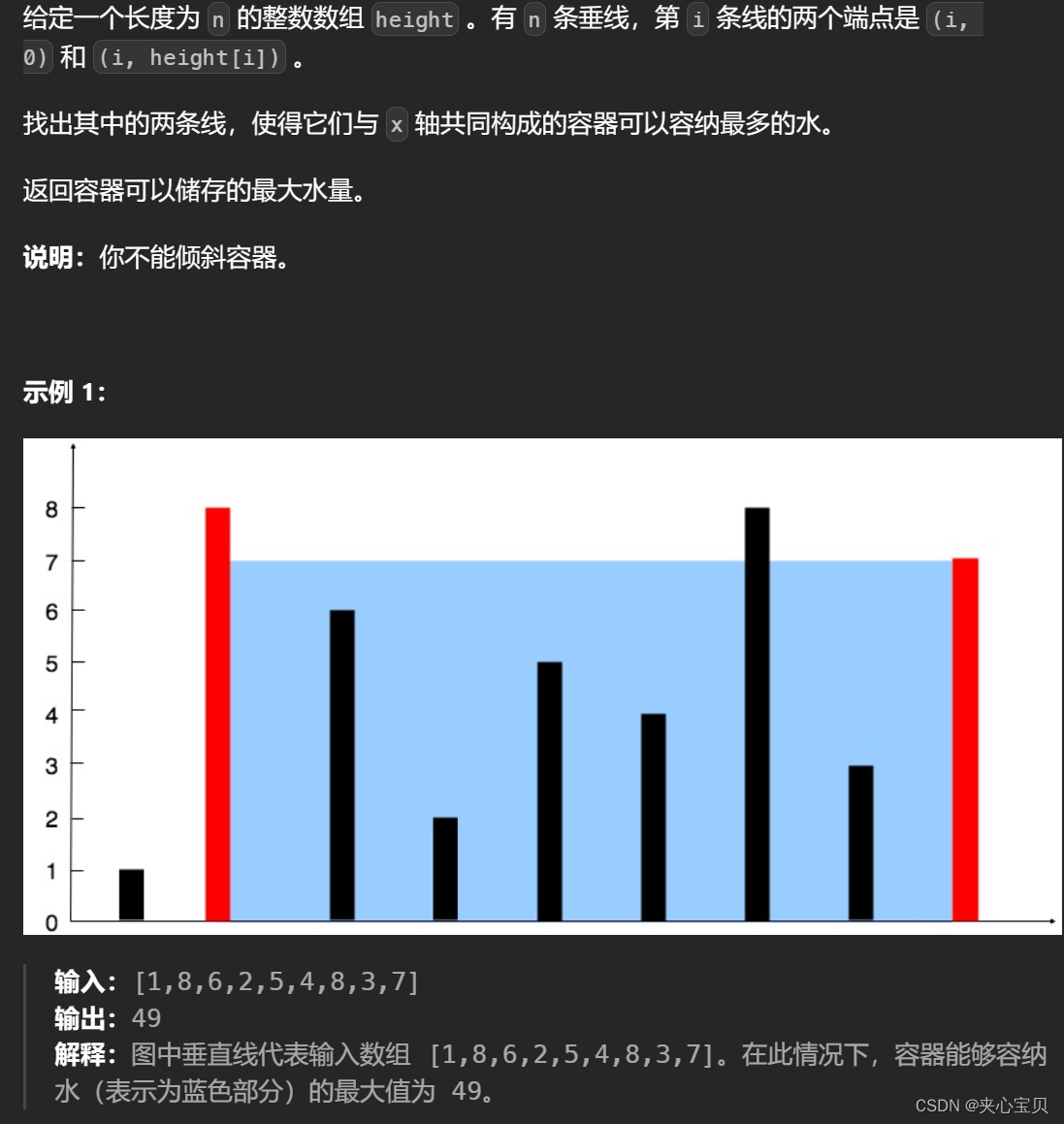
        我们可以固定一边，然后另一边逐渐向右移动，记录每次的面积大小，最后取所有面积中最大的一个。

int maxArea(int* height, int heightSize) {int maxarea = 0;for(int i = 0;i<heightSize-1;i++){for(int j = i+1;j<heightSize;j++){int area = 0;int len = j-i;int heigh = height[i];if(height[j] < height[i])heigh = height[j];area = len * heigh;if(area > maxarea)maxarea = area;}}return maxarea;
}

        暴力求解的时间复杂度为O(n^2)，空间复杂度为O(n)。效率比较低。

        2、双指针

        关键词：左右两边。

        模式识别：需要移动左右两头的，就可以考虑双指针。

        我们将left指针定义在左边，right定义在右边。

        这题的难点在于如何移动双指针？

        首先我们要分析这题的面积是如何算的：

        底长 = right - left，两指针之差；高 = min{ height[left] , height[right] }，两指针位置处数组的较小值。我们一来就将底长固定到最大的，底长我们是固定的，唯一不确定的就是高，所以我们就要从高来下手。

        求最大面积，自然要让高尽可能大，我们就可以让两指针处数组的较小值对应的指针去移动，因为较小值决定了面积的下限。假如 height [ left ]   < height[right]我们就让left去移动，如果left移动到height[left]>height[right]，就让right去移动，反复进行下去；直到left >= right就结束。

        当然我们每次移动的时候也要记录该次面积，和maxarea进行比较，取较大值。

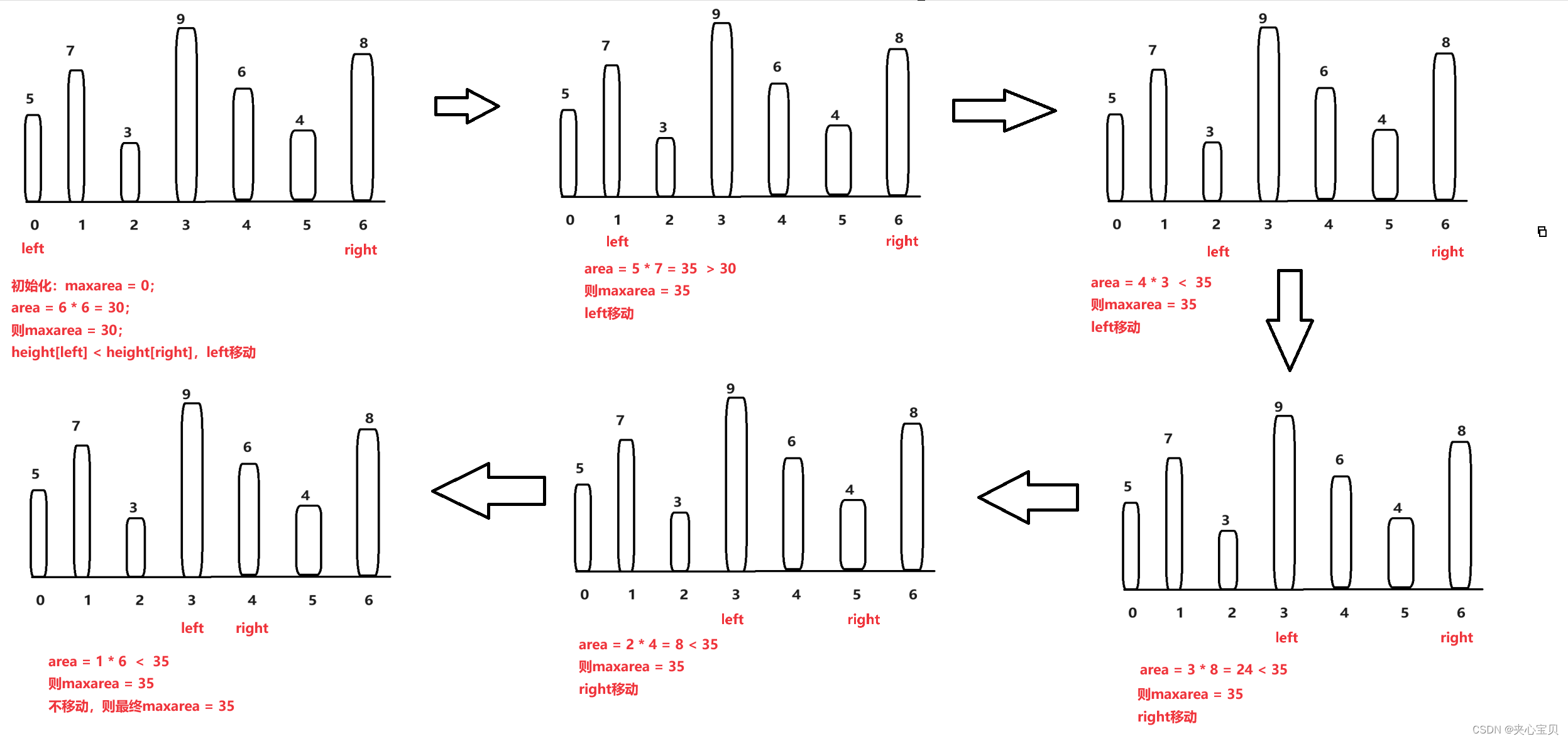
        代码如下：

int maxArea(int* height, int heightSize) {int maxarea = 0, left = 0, right = heightSize - 1;while (left < right) {int len = right - left;int heigh = height[left];if (height[left] > height[right])heigh = height[right];int area = len * heigh;if (area > maxarea)maxarea = area;if (height[left] < height[right])left++;elseright--;}return maxarea;
}