二分算法模版
- 实数二分算法模版
- 实数二分模版题
- 整数二分算法模版
- 向上取整二分模版
- 向下取整二分模版
- 二分模版的注意点
- 二分模版中check函数的实现
- 能够使用二分的条件
二分主要分两类,
一类是对实数进行二分,一类是对整数进行二分
对整数二分又分成2种,一种是向上取整的二分模版,一种是向下取整的二分模版
实数二分算法模版
//这里区间范围为
double l = 0 ,r = n;// 这里循环条件根据题意来,保留几位小数//如果题目要求保留6位小数,保险一点,再加2位,//循环条件就是保留8位小数 --->(r - l)while(r - l > 1e-8) //r - l {double mid = (r + l) / 2;if(check(mid))r = mid; //范围大了,缩小范围else l = mid; //范围小了扩大范围}注意:浮点数二分相当于连续的,要加或者减一个很小的数, +1, -1 误差很大,所以都后面执行语句直接等于mid
区别于实数二分
实数二分模版题
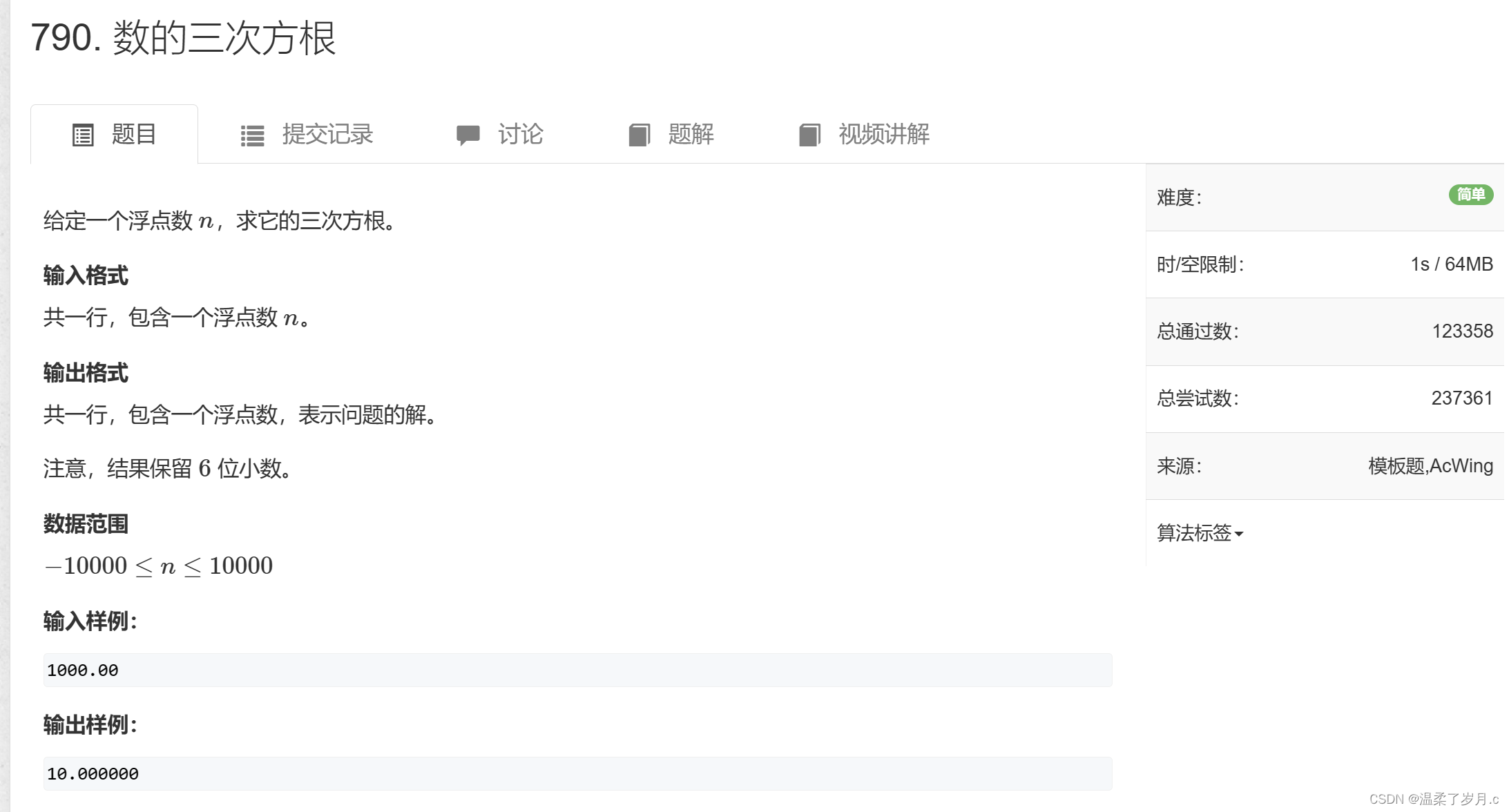
#include<iostream>
#include<cstdio>using namespace std;int main()
{double x;scanf("%lf", &x);double l = -10000 ,r = 10000;while(r - l > 1e-8) //r - l 大于8位小数 (题目要求六位,这里取八位,保险一点){double mid = (r + l) / 2;if(mid * mid * mid >= x)r = mid; //范围大了,缩小范围else l = mid; //范围小了扩大范围}printf("%.6lf", l);return 0;
}
整数二分算法模版
向上取整二分模版
一般,可用来求最小值中的最大值或者最大值
// 每次注意找出二分的范围
//向上取整的区间为 [l, mid - 1] [mid, r]int l = 0, r = n;
while(l < r)
{int mid = l + r + 1 >> 1;if(check(mid)) //mid数据合法,扩大范围,看看有没有更大的l = mid; else //mid数据不合法,缩小范围r = mid - 1
}//结束循环的条件 l == r
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid;,此时为了防止死循环,计算mid时需要加1。
向下取整二分模版
一般,可用来求最大值中的最小值或者最小值
//向下取整的区间范围
//[l, mid] [mid + 1, r]int l = 0, r = n;
while(l < r)
{int mid = l + r >> 1;if(check(mid)) //mid数据合法 缩小区间看看有没有更小的r = mid;else //mid数据不合法,扩大区间 l = mid + 1;
}当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时,其更新操作是r = mid或者l = mid + 1;,计算mid时不需要加1
二分模版的注意点
二分模版有很多,选择自己适合的背就行
这个整数二分的注意点
1.循环条件都是 while(l < r) 都没有取等
2.向上取整的算法模版中 mid 还有多加1, 不加1的话会陷入死循环
3.二分使用的时候,是对一个有序的区间进行二分,如果这个区间无序,要对这个区间=进行排序
二分模版中check函数的实现
.check()函数的实现
check()函数,是二分模版中,最难的一部分。
作用就是判断二分的数据是否合法,满足题意
或者是找具有二段性的临界的判断条件
不同题的check函数都是不一样的,这只有靠自己做题,多积累,多体会和总结
能够使用二分的条件
能够使用二分解决问题,一般是具有单调性或者是二分性,或者是求一个区间的最大值或者最小值等



![【C++入门到精通】特殊类的设计 |只能在堆 ( 栈 ) 上创建对象的类 |禁止拷贝和继承的类 [ C++入门 ]](https://img-blog.csdnimg.cn/direct/32ed20b44d704746a77da19b16d060e5.jpeg)