clc
clear
close all距离向参数
R_eta_c = 20e3; % 景中心斜距
Tr = 25e-6; % 发射脉冲时宽
Kr = 0.25e12; % 距离向调频率
Fr = 7.5e6; % 距离向采样率
Nrg = 256; % 距离线采样点数
Bw = abs(Kr*Tr); % 距离信号带宽方位向参数
Delta_f_dop = 80; % 多普勒带宽
Fa = 104; % 方位向采样率
Naz = 256; % 距离线数;
theta_sq_c = [0,22.8]; % 波束斜视角
eta_c = [0,-51.7]; % 波束中心偏移时间
f_eta_c = [0,2055]; % 多普勒中心频率
Vr = 150; % 等效速度其他参数
c = 3e8;
f0 = 5.3e9;
lambda = c/f0;
R0 = R_eta_c*cosd(theta_sq_c(2)); % 最短斜距
La = 0.886*(2*Vr*cosd(theta_sq_c(2)))/Delta_f_dop; % 真实孔径
theta_bw = 0.886*lambda/La; % 方位向波束宽度
Trr = Nrg/Fr; % 发射脉冲时宽
Taa = Naz/Fa; % 目标照射时间
Ka = 2*Vr^2*cosd(theta_sq_c(2))^2/lambda/R0; % 方位向调频率
d_t_tau = 1/Fr; % 距离采样时间间隔
d_t_eta = 1/Fa; % 方位采样时间间隔
d_f_tau = Fa/Nrg; % 距离采样频率间隔
d_f_eta = Fa/Naz; % 方位采样频率间隔变量设置
tau = (-Trr/2:d_t_tau:Trr/2-d_t_tau)+2*R_eta_c/c; % 距离时间变量
eta = (-Taa/2:d_t_eta:Taa/2-d_t_eta)+eta_c(2); % 方位时间变量坐标设置
[tauX,etaY] = meshgrid(tau,eta); % 二维网格坐标 信号设置
% R_eta = R0+Vr^2*etaY.^2/2/R0; % 瞬时斜距
R_eta = sqrt(R0^2 + Vr^2*etaY.^2);
A0 = 1; % 后向散射系数幅度
wr = (abs(tauX-2*R_eta/c) <= Tr/2); % 距离向包络
wa = sinc(0.886*atan(Vr*(etaY-eta_c(2))/R0)/theta_bw).^2; % 方位包络
srt = A0*wr.*wa.*exp(-1j*4*pi*f0*R_eta/c)....*exp(+1j*pi*Kr*(tauX-2*R_eta/c).^2);
srt_z = A0*wr.*wa.*exp(-1j*4*pi*f0*R_eta/c)... .*exp(+1j*pi*Kr*(tauX-2*R_eta/c).^2);% 正扫频
srt_f = A0*wr.*wa.*exp(-1j*4*pi*f0*R_eta/c)... .*exp(-1j*pi*Kr*(tauX-2*R_eta/c).^2);% 负扫频
% srt = A0*wr.*wa.*exp(-1j*4*pi*R0/lambda)...
% .*exp(-1j*pi*Ka*etaY.^2)...
% .*exp(1j*pi*Kr*(tauX-2*R_eta/c).^2);
% srt_z = A0*wr.*wa.*exp(-1j*4*pi*R0/lambda)...
% .*exp(-1j*pi*Ka*etaY.^2)...
% .*exp(1j*pi*Kr*(tauX-2*R_eta/c).^2); % 正扫频
% srt_f = A0*wr.*wa.*exp(-1j*4*pi*R0/lambda)...
% .*exp(-1j*pi*Ka*etaY.^2)...
% .*exp(-1j*pi*Kr*(tauX-2*R_eta/c).^2); % 负扫频
Srf_rd = fft(srt_z);
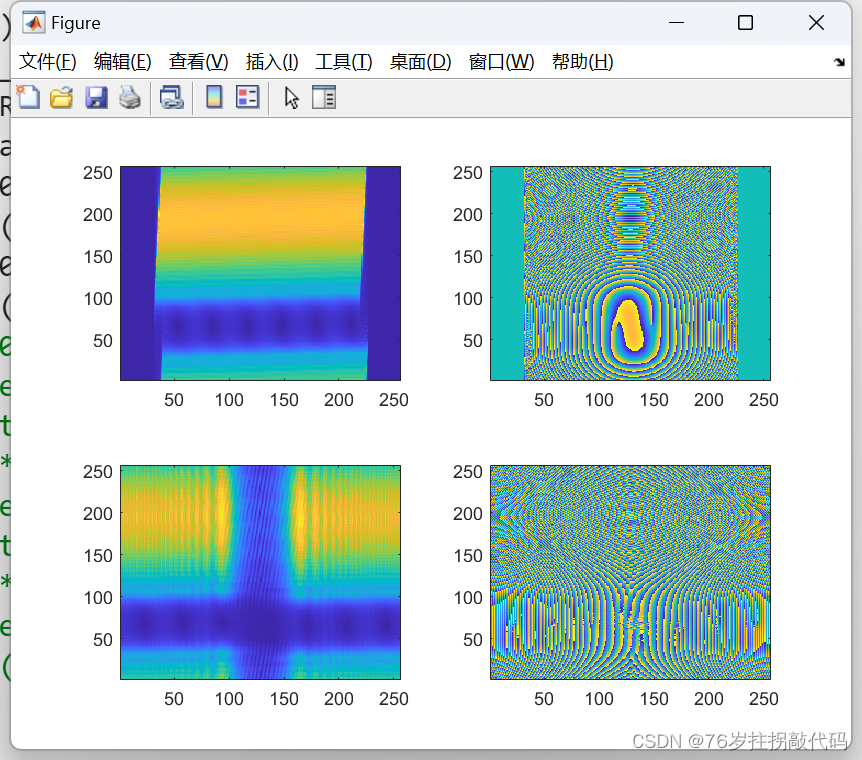
Srf_2d = fft2(srt_z);绘图
figure,subplot(221)
imagesc(abs(Srf_rd)),set(gca, 'YDir', 'normal')
subplot(222)
imagesc(angle(Srf_rd)),set(gca, 'YDir', 'normal')
subplot(223)
imagesc(abs(Srf_2d)),set(gca, 'YDir', 'normal')
subplot(224)
imagesc(angle(Srf_2d)),set(gca, 'YDir', 'normal')