粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,它通过模拟鸟群或鱼群的行为来寻找最优解。在泊位调度问题中,目标是最小化所有船只在港时间的总和,而PSO算法可以帮助我们找到一个较优的调度方案。
泊位调度问题是指在有限数量的泊位资源下,安排船只的到港和离港时间,以最小化船只在港等待的时间。该问题存在多个约束条件,如泊位容量、船只到港和离港时间窗口等。
PSO算法的核心思想是通过模拟粒子在解空间中的移动来搜索最优解。每个粒子代表一个解,并根据自身的历史最佳解和群体的历史最佳解进行调整。粒子根据自身和邻域最优解的信息更新速度和位置,以逐渐靠近最优解。
在泊位调度问题中,每个粒子的位置可以表示为一个泊位调度方案,其中每个船只被分配到一个特定的泊位,并确定其到港和离港时间。粒子的速度和位置更新规则可以根据目标函数来定义,以使船只在港时间的总和最小化。
PSO算法的优点在于简单且易于实现,能够在高维解空间中找到较优解。然而,对于泊位调度问题这样的复杂问题,PSO算法可能会陷入局部最优解。为了克服这个问题,可以采用多种改进方法,如引入局部搜索机制或组合其他优化算法。
总结而言,粒子群算法是一种有效的优化算法,适用于解决泊位调度问题。通过调整粒子的速度和位置,并结合合适的目标函数,可以找到一个较优的泊位调度方案,以最小化船只在港时间的总和。然而,对于复杂的问题,仍然需要进一步的研究和改进。
流程如下:



数据:
停泊时间:
| 船舶泊位 | 1# | 2# | 3# | 4# | 5# | 6# |
| 船1 | 3 | 3 | 3.290323 | 3.290323 | 3.290323 | 3.290323 |
| 船2 | 3.29 | 3.29 | 3.608387 | 3.608387 | 3.608387 | 3.608387 |
| 船3 | 3.35 | 3.35 | 3.674194 | 3.674194 | 3.674194 | 3.674194 |
| 船4 | 5 | 5 | 5.483871 | 5.483871 | 5.483871 | 5.483871 |
| 船5 | 1.94 | 1.94 | 2.127742 | 2.127742 | 2.127742 | 2.127742 |
| 船6 | 1.45 | 1.45 | 1.590323 | 1.590323 | 1.590323 | 1.590323 |
| 船7 | 0.97 | 0.97 | 1.063871 | 1.063871 | 1.063871 | 1.063871 |
| 船8 | 4.61 | 4.61 | 5.056129 | 5.056129 | 5.056129 | 5.056129 |
| 船9 | 5.06 | 5.06 | 5.549677 | 5.549677 | 5.549677 | 5.549677 |
| 船10 | 7.29 | 7.29 | 7.995484 | 7.995484 | 7.995484 | 7.995484 |
| 船11 | 2.68 | 2.68 | 2.939355 | 2.939355 | 2.939355 | 2.939355 |
| 船12 | 5.74 | 5.74 | 6.295484 | 6.295484 | 6.295484 | 6.295484 |
| 船13 | 0.65 | 0.65 | 0.712903 | 0.712903 | 0.712903 | 0.712903 |
| 船14 | 1.26 | 1.26 | 1.381935 | 1.381935 | 1.381935 | 1.381935 |
| 船15 | 0.81 | 0.81 | 0.888387 | 0.888387 | 0.888387 | 0.888387 |
| 船16 | 1.58 | 1.58 | 1.732903 | 1.732903 | 1.732903 | 1.732903 |
| 船17 | 0.77 | 0.77 | 0.844516 | 0.844516 | 0.844516 | 0.844516 |
| 船18 | 1 | 1 | 1.096774 | 1.096774 | 1.096774 | 1.096774 |
| 船19 | 3.1 | 3.1 | 3.4 | 3.4 | 3.4 | 3.4 |
| 船20 | 0.71 | 0.71 | 0.77871 | 0.77871 | 0.77871 | 0.77871 |
| 船21 | 0.97 | 0.97 | 1.063871 | 1.063871 | 1.063871 | 1.063871 |
| 船22 | 3.23 | 3.23 | 3.542581 | 3.542581 | 3.542581 | 3.542581 |
到港时间
| 到港时间 | 装卸量 |
| 0:00 | 93 |
| 3:00 | 102 |
| 3:20 | 104 |
| 3:20 | 155.25 |
| 6:00 | 60 |
| 6:00 | 45 |
| 6:20 | 30 |
| 8:00 | 143 |
| 8:00 | 157 |
| 9:00 | 226 |
| 10:00 | 83 |
| 10:30 | 178 |
| 11:00 | 20 |
| 12:00 | 39 |
| 12:00 | 25 |
| 14:40 | 49 |
| 14:40 | 24 |
| 15:00 | 31 |
| 15:00 | 96 |
| 18:50 | 22 |
| 21:10 | 30 |
| 22:00 | 100 |
装卸速度
| 装卸速度 | |
| 泊位1 | 31 |
| 泊位2 | 31 |
| 泊位3 | 34 |
| 泊位4 | 35 |
| 泊位5 | 36 |
| 泊位6 | 37 |
程序结果:
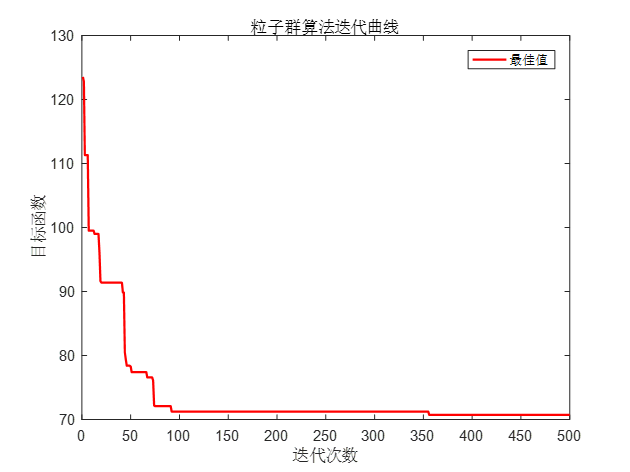

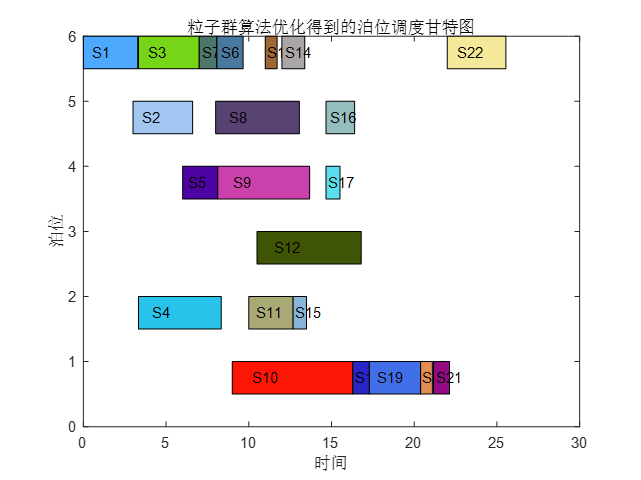
粒子群算法优化得到最优成本
Valuebest =
70.7209677419355
粒子群算法优化得到最优粒子
psobest =
1 至 6 列
-1 -0.276376816044633 0.0110834051789061 -0.588322236509362 -0.871896419169566 1
7 至 12 列
0.882043641594225 0.394648902367656 0.649790379151507 -1 -0.0590250701437167 -1
13 至 18 列
1 1 0.941078162307071 1 0.925858029802935 -0.755714050637173
19 至 24 列
0.642324983266078 1 1 1 6.33758011393659 5.85939735126611
25 至 30 列
6.99 2.49649225428723 4.78659200827198 6.99 6.99 5.21051862147312
31 至 36 列
4.23951824644256 1 2.42088917195685 3.73458639406582 6.99 6.99
37 至 42 列
2.24808981777205 5.21345040727043 4.55442530362547 1.11174406517414 1 1
43 至 44 列
1.69713330740672 6.04705817521954
y =
70.7209677419355
G =
1 6 0 3.29032258064516
10 1 9 16.29
12 3 10.5 16.7954838709677
5 4 6 8.12774193548387
18 1 16.29 17.29
4 2 3.33333333333333 8.33333333333333
2 5 3 6.60838709677419
11 2 10 12.68
3 6 3.33333333333333 7.00752688172043
8 5 8 13.0561290322581
19 1 17.29 20.39
9 4 8.12774193548387 13.6774193548387
7 6 7.00752688172043 8.07139784946237
17 4 14.6666666666667 15.5111827956989
15 2 12.68 13.49
6 6 8.07139784946237 9.66172043010753
13 6 11 11.7129032258064
14 6 12 13.381935483871
16 5 14.6666666666667 16.3995698924731
20 1 20.39 21.1
21 1 21.1666666666667 22.1366666666667
22 6 22 25.5425806451613
Stime =
0 3.29032258064516
3 6.60838709677419
3.33333333333333 7.00752688172043
3.33333333333333 8.33333333333333
6 8.12774193548387
8.07139784946237 9.66172043010753
7.00752688172043 8.07139784946237
8 13.0561290322581
8.12774193548387 13.6774193548387
9 16.29
10 12.68
10.5 16.7954838709677
11 11.7129032258064
12 13.381935483871
12.68 13.49
14.6666666666667 16.3995698924731
14.6666666666667 15.5111827956989
16.29 17.29
17.29 20.39
20.39 21.1
21.1666666666667 22.1366666666667
22 25.5425806451613
S =
1 10 12 5 18 4 2 11 3 8 19 9 7 17 15 6 13 14 16 20 21 22
T =
6 5 6 2 4 6 6 5 4 1 2 3 6 6 2 5 4 1 1 1 1 6
Stime =
0 3.29032258064516
3 6.60838709677419
3.33333333333333 7.00752688172043
3.33333333333333 8.33333333333333
6 8.12774193548387
8.07139784946237 9.66172043010753
7.00752688172043 8.07139784946237
8 13.0561290322581
8.12774193548387 13.6774193548387
9 16.29
10 12.68
10.5 16.7954838709677
11 11.7129032258064
12 13.381935483871
12.68 13.49
14.6666666666667 16.3995698924731
14.6666666666667 15.5111827956989
16.29 17.29
17.29 20.39
20.39 21.1
21.1666666666667 22.1366666666667
22 25.5425806451613
>>