西瓜书学习笔记——层次聚类（公式推导+举例应用）-编程知识

西瓜书学习笔记——层次聚类（公式推导+举例应用）

文章目录

- - 算法介绍
  - 实验分析

算法介绍

层次聚类是一种将数据集划分为层次结构的聚类方法。它主要有两种策略：自底向上和自顶向下。
其中AGNES算法是一种自底向上聚类算法，用于将数据集划分为层次结构的聚类。算法的基本思想是从每个数据点开始，逐步合并最相似的簇，直到形成一个包含所有数据点的大簇。这个过程被反复执行，构建出一个层次化的聚类结构。这其中的关键就是如何计算聚类簇之间的距离。 但实际上，每个簇都是一个集合，故我们只需要计算集合与集合的距离即可。例如，给定聚类簇 $C_i$ 与 $C_j$ ，可通过下面的式子来计算距离：
$d_{min}(C_i,C_j)=\underset{x \in C_i,z\in C_j}{\text{min}} \ dist(x,z) \tag{1}$
$d_{max}(C_i,C_j)=\underset{x \in C_i,z\in C_j}{\text{max}} \ dist(x,z) \tag{2}$
$d_{avg }(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in c_j} dist(x,z) \tag{3}$

其中 $C_i|$ 是集合 $C_i$ 的元素个数。显然最小距离是由两个簇最近的样本点决定的；最大距离是由两个簇最远的样本点决定的；平均距离是由两个簇所有样本点共同决定的。

还有个更有效的计算集合距离的方法豪斯多夫距离：假设在同一样本空间的集合 $X$ 与 $Z$ 之间的距离可以通过以下式子计算：
$\operatorname{dist}_{\mathrm{H}}(X, Z)=\max \left(\operatorname{dist}_{\mathrm{h}}(X, Z), \operatorname{dist}_{\mathrm{h}}(Z, X)\right) \tag{4}$

其中 $\operatorname{dist}_{\mathrm{h}}(X, Z)=\max _{\boldsymbol{x} \in X} \min _{\boldsymbol{z} \in Z}\|\boldsymbol{x}-\boldsymbol{z}\|_2$

豪斯多夫距离的应用涉及到形状匹配、图像匹配、模式识别等领域，它对于描述两个集合的整体形状之间的差异具有较好的效果。然而，由于计算豪斯多夫距离涉及到点之间的一一匹配，因此在实际应用中可能需要考虑一些优化算法以提高计算效率。

下图是AGNES算法流程图：
在这里插入图片描述

实验分析

数据集如下表所示：
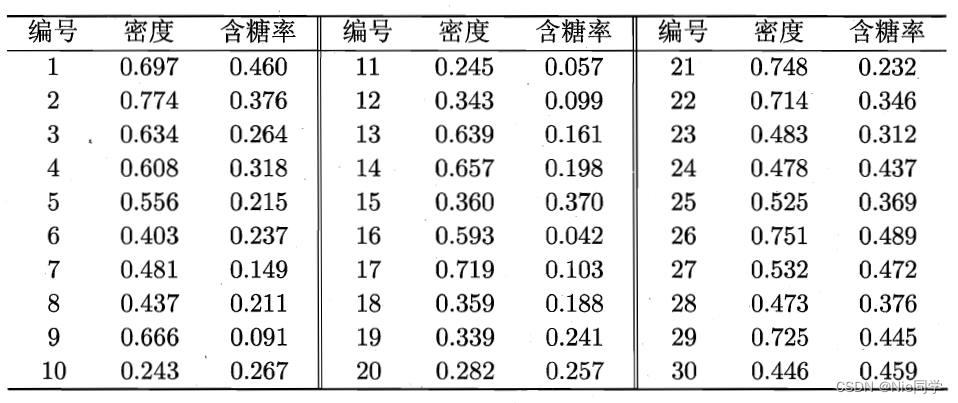
在这里插入图片描述
读入数据集：

import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdata = pd.read_csv('data/4.0.csv')

定义距离函数：

# 定义豪斯多夫距离函数
def hausdorff_distance(cluster1, cluster2):max_distance1 = max(min(distance(p1, p2) for p1 in cluster1) for p2 in cluster2)max_distance2 = max(min(distance(p1, p2) for p2 in cluster2) for p1 in cluster1)return max(max_distance1, max_distance2)# 定义距离函数
def distance(point1, point2):return ((point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2) ** 0.5

AGNES算法：

# AGNES算法
def agnes(data):clusters = [[point] for point in data.values]while len(clusters) > 4:min_distance = float('inf')merge_indices = (0, 0)for i in range(len(clusters)):for j in range(i + 1, len(clusters)):cluster1 = clusters[i]cluster2 = clusters[j]current_distance = hausdorff_distance(cluster1, cluster2)if current_distance < min_distance:min_distance = current_distancemerge_indices = (i, j)# 合并最近的两个簇merged_cluster = clusters[merge_indices[0]] + clusters[merge_indices[1]]clusters.pop(merge_indices[1])clusters[merge_indices[0]] = merged_clusterreturn clusters

绘制分类结果函数：

# 绘制分类结果
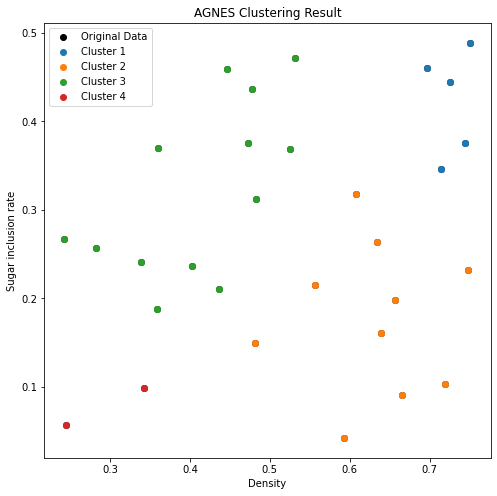
def plot_clusters(data, clusters):plt.figure(figsize=(8, 8))# 绘制原始数据点plt.scatter(data['Density'], data['Sugar inclusion rate'], color='black', label='Original Data')# 绘制分类结果for i, cluster in enumerate(clusters):cluster_data = pd.DataFrame(cluster, columns=['Density', 'Sugar inclusion rate'])plt.scatter(cluster_data['Density'], cluster_data['Sugar inclusion rate'], label=f'Cluster {i + 1}')# 添加标签和图例plt.title('AGNES Clustering Result')plt.xlabel('Density')plt.ylabel('Sugar inclusion rate')plt.legend()plt.show()

执行AGNES且画出分类结果：

# 执行层次聚类
result_clusters = agnes(data)# 输出聚类结果
for i, cluster in enumerate(result_clusters):print(f'Cluster {i + 1}: {cluster}')# 绘制分类结果图
plot_clusters(data, result_clusters)