一、题目

给定一个含有n个正整数的数组和一个正整数target。找出该数组中满足其总和大于等于target的长度最小的连续子数组[numsl, numsl+1, ..., numsr-1, numsr]，并返回其长度。如果不存在符合条件的子数组，返回0。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组[4,3]是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

::: warning
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
:::

进阶： 如果你已经实现O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。

二、代码

【1】滑动窗口： 定义两个指针fast和slow分别表示子数组（滑动窗口窗口）的开始位置和结束位置，维护变量sum存储子数组中的元素和（即从nums[fast]到nums[slow]的元素和）。初始状态下，fast和slow都指向下标0，sum的值为0。每一轮迭代，将nums[fast]加到 sum，如果sum≥target，则更新子数组的最小长度（此时子数组的长度是fast-slow+1，然后将nums[slow]从sum中减去并将start右移，直到sum<target，在此过程中同样更新子数组的最小长度。在每一轮迭代的最后，将fast右移。

class Solution {public int minSubArrayLen(int target, int[] nums) {// 思路：1、指定快慢两个指针 fast slow // 2、fast 先移动，如果 sum > target ， slow 先前走一步int fast = 0, slow = 0, sum = 0, min = Integer.MAX_VALUE;while (fast < nums.length) {sum += nums[fast];while (sum >= target) {min = Math.min(min, fast - slow + 1);sum-=nums[slow];++slow;}++fast;}return min == Integer.MAX_VALUE ? 0 : min;}
}

时间复杂度： O(n)，其中n是数组的长度。指针fast和slow最多各移动n次。
空间复杂度： O(1)

【2】前缀和 + 二分查找： 为了使用二分查找，需要额外创建一个数组sums用于存储数组nums的前缀和，其中sums[i]表示从nums[0]到nums[i−1]的元素和。得到前缀和之后，对于每个开始下标i，可通过二分查找得到大于或等于i的最小下标index，使得sums[index]−sums[i−1]≥target，并更新子数组的最小长度（此时子数组的长度是index(i−1)）。因为这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正，这里就不能使用二分来查找这个位置了。

在很多语言中，都有现成的库和函数来为我们实现这里二分查找大于等于某个数的第一个位置的功能，比如C++的lower_bound，Java中的Arrays.binarySearch，C#中的Array.BinarySearch，Python中的bisect.bisect_left。但是有时面试官可能会让我们自己实现一个这样的二分查找函数。

class Solution {public int minSubArrayLen(int target, int[] nums) {
return min == Integer.MAX_VALUE ? 0 : min;// 思路：1、新创建一个数组，保存i之前数据和；// 2、根据二分查找，获取到大于target的第一个下标；int[] sums = new int[nums.length + 1];int min = Integer.MAX_VALUE;for (int i = 1; i <= nums.length; i++) {sums[i] = sums[i - 1] + nums[i - 1];}for (int i = 1; i <= nums.length; i++) {int tarTemp = sums[i - 1] + target;int index = Arrays.binarySearch(sums, tarTemp);if (index < 0) {index = -index - 1;}// 找到了if (index <= nums.length) {min = Math.min(min, index - (i - 1));}}return min == Integer.MAX_VALUE ? 0 : min;}
}

时间复杂度： O(nlog⁡n)，其中n是数组的长度。需要遍历每个下标作为子数组的开始下标，遍历的时间复杂度是O(n)，对于每个开始下标，需要通过二分查找得到长度最小的子数组，二分查找得时间复杂度是O(log⁡n)，因此总时间复杂度是O(nlog⁡n)。
空间复杂度： O(n)，其中n是数组的长度。额外创建数组sums存储前缀和。

【3】暴力解法： 初始化子数组的最小长度为无穷大，枚举数组nums中的每个下标作为子数组的开始下标，对于每个开始下标i，需要找到大于或等于i的最小下标j，使得从nums[i]到nums[j]的元素和大于或等于s，并更新子数组的最小长度（此时子数组的长度是j−i+1）。

class Solution {public int minSubArrayLen(int target, int[] nums) {// 思路：1、定义返回值 res = max, 在循环中获取符合要求的最小长度，存入res中。求最小数时，返回值默认时 Integer的最大值；// 2、第一层for循环保证所有的数据都能够被遍历依次，作为left指针// 3、第二层for循环中，遍历left后的元素，找到第一个符合要求的子数组，也就是最小长度的子数组，直接退出；int res = Integer.MAX_VALUE;for(int i = 0; i < nums.length; i++) {// 第一层遍历之前需要重新定义int sum = 0;for(int j = i; j < nums.length; j++) {sum += nums[j];if (sum >= target) {res = Math.min(res, j - i + 1);break;}}}return res == Integer.MAX_VALUE ? 0 : res;}
}

时间复杂度： O(n2)，其中n是数组的长度。需要遍历每个下标作为子数组的开始下标，对于每个开始下标，需要遍历其后面的下标得到长度最小的子数组。
空间复杂度： O(1)

【4】使用队列相加（实际上我们也可以把它称作是滑动窗口，这里的队列其实就相当于一个窗口）： 我们把数组中的元素不停的入队，直到总和大于等于s为止，接着记录下队列中元素的个数，然后再不停的出队，直到队列中元素的和小于s为止（如果不小于s，也要记录下队列中元素的个数，这个个数其实就是不小于s的连续子数组长度，我们要记录最小的即可）。接着再把数组中的元素添加到队列中……重复上面的操作，直到数组中的元素全部使用完为止。
这里以[2,3,1,2,4,3]举例画个图来看下

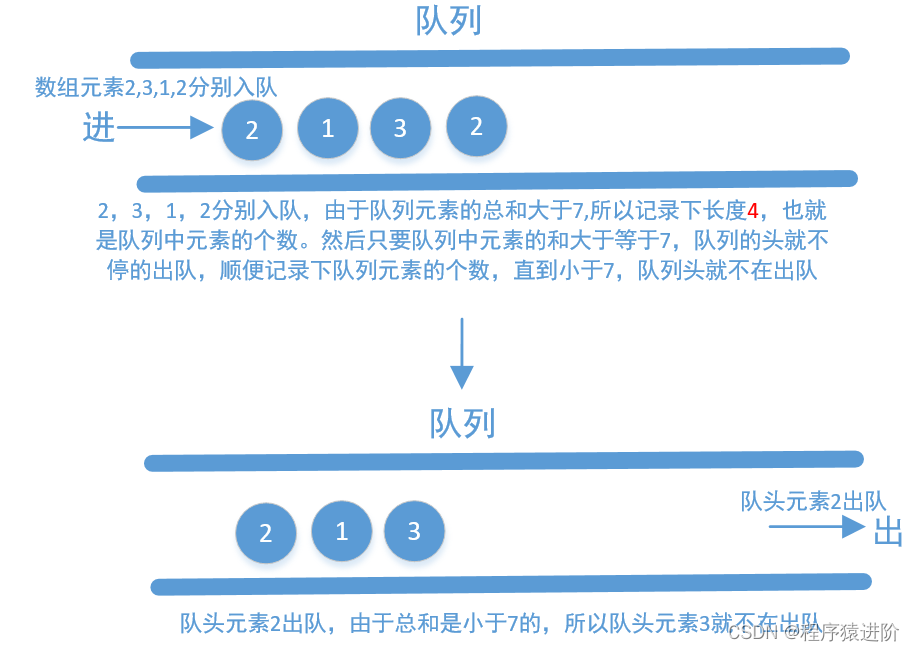
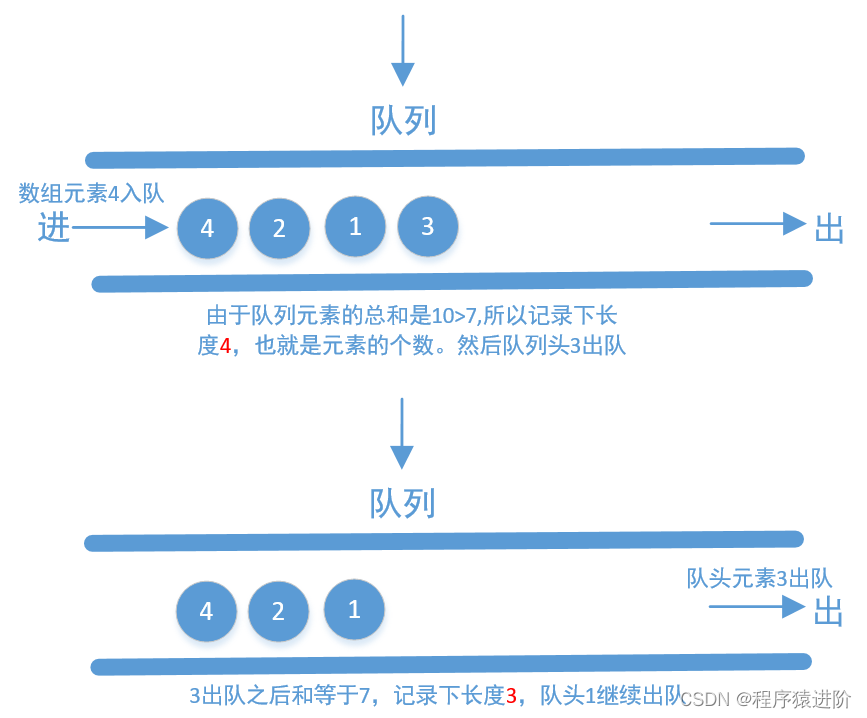
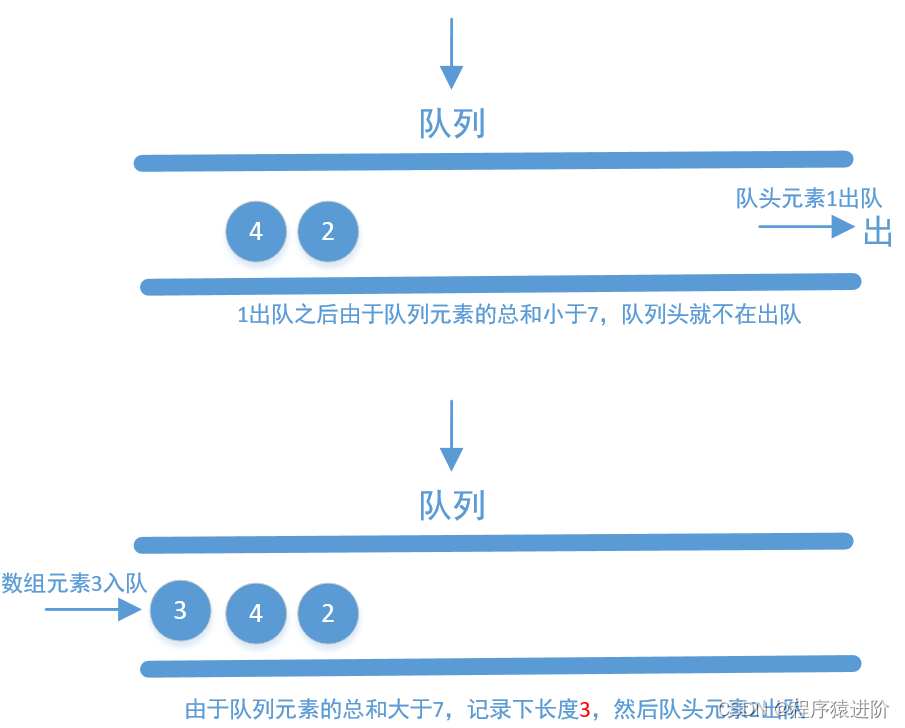
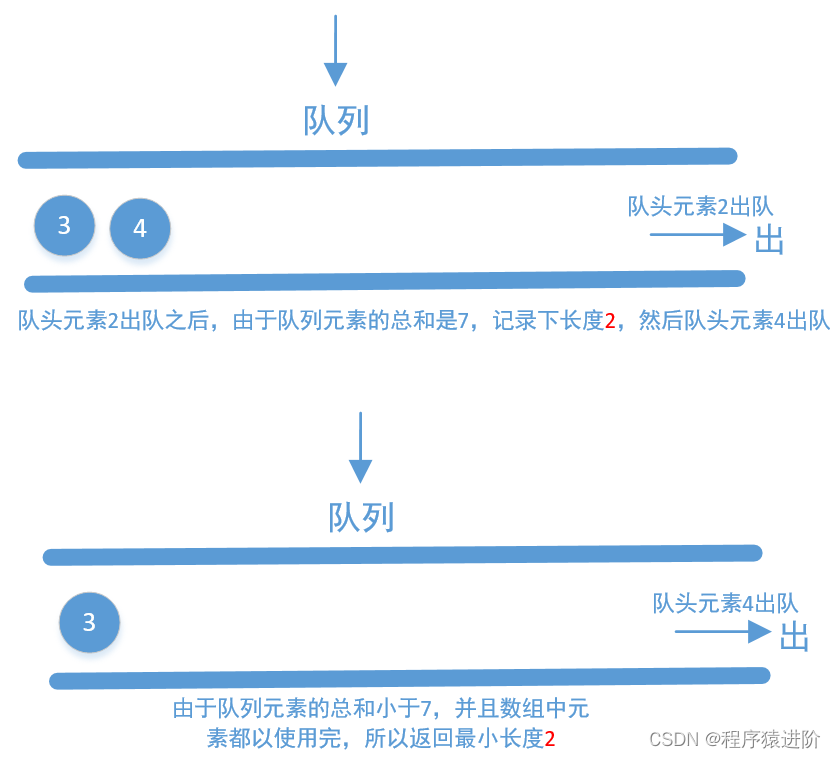
上面画的是使用队列，但在代码中我们不直接使用队列，我们使用两个指针，一个指向队头一个指向队尾，我们来看下代码

public int minSubArrayLen(int s, int[] nums) {int lo = 0, hi = 0, sum = 0, min = Integer.MAX_VALUE;while (hi < nums.length) {sum += nums[hi++];while (sum >= s) {min = Math.min(min, hi - lo);sum -= nums[lo++];}}return min == Integer.MAX_VALUE ? 0 : min;
}