hough检测原理

点击图像处理之Hough变换检测直线查看
下面直接描述检测圆形的方法

基于Hough变换的圆形检测方法

对于一个半径为 $r$ ，圆心为 $（ a, b ）$ 的圆，我们将其表示为：
$x-a)^2+(y-b)^2=r^2$
此时 $x=[x,y]^T，a=[a,b,r]^T$ ，其参数空间为三维。显然，图像空间上的一点 $（ x, y ）$ ，在参数空间中对应着一个圆锥，如下图所示。
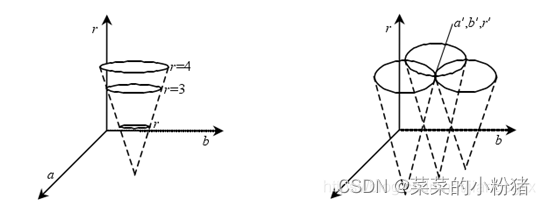
在这里插入图片描述
而图像空间的一个圆就对应着这一簇圆锥相交的一个点，这个特定点在参数空间的三维参数一定，就表示一定半径一定圆心坐标的图像空间的那个圆。
上述方法是经典的Hough圆检测方法的原理，它具有精度高，抗干扰能力强等优点，但由于该方法的参数空间为三维，要在三维空间上进行证据累计的话，需要的时间和空间都是庞大的，在实际应用中不适用。为加快Hough变换检测圆的速度，学者们进行了大量研究，也出现了很多改进的Hough变换检测圆的方法。如利用图像梯度信息的Hough变换，对圆的标准方程对x求导得到下式：
$2(x-a)+2(y-b)\frac{dy}{dx}=0$
从上式看出，此时的参数空间从半径 $r$ ，圆心 $（ a, b ）$ 三维，变成了只有圆心 $（ a, b ）$ 的二维空间，利用这种方法检测圆其计算量明显减少了。
但这种改进的Hough变换检测圆的方法其检测精度并不高，原因在于，此种方法利用了边界斜率。
从本质上讲，边界斜率其实是用曲线在某一点的弦的斜率来代替的，这种情况下，要保证不存在误差，只有在弦长为零的情况。但在数字图像中，曲线的表现形式是离散的，其在某一点处的斜率指的是此点右向n步斜率或是左向n步斜率。如果弦长过小了，斜率的量化误差就会增大。这种方法比较适用于干扰较少的完整圆形目标。
在这里插入图片描述

主要代码：

def AHTforCircles(edge,center_threhold_factor = None,score_threhold = None,min_center_dist = None,minRad = None,maxRad = None,center_axis_scale = None,radius_scale = None,halfWindow = None,max_circle_num = None):if center_threhold_factor == None:center_threhold_factor = 10.0if score_threhold == None:score_threhold = 15.0if min_center_dist == None:min_center_dist = 80.0if minRad == None:minRad = 0.0if maxRad == None:maxRad = 1e7*1.0if center_axis_scale == None:center_axis_scale = 1.0if radius_scale == None:radius_scale = 1.0if halfWindow == None:halfWindow = 2if max_circle_num == None:max_circle_num = 6min_center_dist_square = min_center_dist**2sobel_kernel_y = np.array([[-1.0, -2.0, -1.0], [0.0, 0.0, 0.0], [1.0, 2.0, 1.0]])sobel_kernel_x = np.array([[-1.0, 0.0, 1.0], [-2.0, 0.0, 2.0], [-1.0, 0.0, 1.0]])edge_x = convolve(sobel_kernel_x,edge,[1,1,1,1],[1,1])edge_y = convolve(sobel_kernel_y,edge,[1,1,1,1],[1,1])center_accumulator = np.zeros((int(np.ceil(center_axis_scale*edge.shape[0])),int(np.ceil(center_axis_scale*edge.shape[1]))))k = np.array([[r for c in range(center_accumulator.shape[1])] for r in range(center_accumulator.shape[0])])l = np.array([[c for c in range(center_accumulator.shape[1])] for r in range(center_accumulator.shape[0])])minRad_square = minRad**2maxRad_square = maxRad**2points = [[],[]]edge_x_pad = np.pad(edge_x,((1,1),(1,1)),'constant')edge_y_pad = np.pad(edge_y,((1,1),(1,1)),'constant')Gaussian_filter_3 = 1.0 / 16 * np.array([(1.0, 2.0, 1.0), (2.0, 4.0, 2.0), (1.0, 2.0, 1.0)])for i in range(edge.shape[0]):for j in range(edge.shape[1]):if not edge[i,j] == 0:dx_neibor = edge_x_pad[i:i+3,j:j+3]dy_neibor = edge_y_pad[i:i+3,j:j+3]dx = (dx_neibor*Gaussian_filter_3).sum()dy = (dy_neibor*Gaussian_filter_3).sum()if not (dx == 0 and dy == 0):t1 = (k/center_axis_scale-i)t2 = (l/center_axis_scale-j)t3 = t1**2 + t2**2temp = (t3 > minRad_square)&(t3 < maxRad_square)&(np.abs(dx*t1-dy*t2) < 1e-4)center_accumulator[temp] += 1points[0].append(i)points[1].append(j)M = center_accumulator.mean()for i in range(center_accumulator.shape[0]):for j in range(center_accumulator.shape[1]):neibor = \center_accumulator[max(0, i - halfWindow + 1):min(i + halfWindow, center_accumulator.shape[0]),max(0, j - halfWindow + 1):min(j + halfWindow, center_accumulator.shape[1])]if not (center_accumulator[i,j] >= neibor).all():center_accumulator[i,j] = 0# 非极大值抑制plt.imshow(center_accumulator,cmap='gray')plt.axis('off')plt.show()center_threshold = M * center_threhold_factorpossible_centers = np.array(np.where(center_accumulator > center_threshold))  # 阈值化sort_centers = []for i in range(possible_centers.shape[1]):sort_centers.append([])sort_centers[-1].append(possible_centers[0,i])sort_centers[-1].append(possible_centers[1,i])sort_centers[-1].append(center_accumulator[sort_centers[-1][0],sort_centers[-1][1]])sort_centers.sort(key=lambda x:x[2],reverse=True)centers = [[],[],[]]points = np.array(points)for i in range(len(sort_centers)):radius_accumulator = np.zeros((int(np.ceil(radius_scale * min(maxRad, np.sqrt(edge.shape[0] ** 2 + edge.shape[1] ** 2)) + 1))),dtype=np.float32)if not len(centers[0]) < max_circle_num:breakiscenter = Truefor j in range(len(centers[0])):d1 = sort_centers[i][0]/center_axis_scale - centers[0][j]d2 = sort_centers[i][1]/center_axis_scale - centers[1][j]if d1**2 + d2**2 < min_center_dist_square:iscenter = Falsebreakif not iscenter:continuetemp = np.sqrt((points[0,:] - sort_centers[i][0] / center_axis_scale) ** 2 + (points[1,:] - sort_centers[i][1] / center_axis_scale) ** 2)temp2 = (temp > minRad) & (temp < maxRad)temp = (np.round(radius_scale * temp)).astype(np.int32)for j in range(temp.shape[0]):if temp2[j]:radius_accumulator[temp[j]] += 1for j in range(radius_accumulator.shape[0]):if j == 0 or j == 1:continueif not radius_accumulator[j] == 0:radius_accumulator[j] = radius_accumulator[j]*radius_scale/np.log(j) #radius_accumulator[j]*radius_scale/jscore_i = radius_accumulator.argmax(axis=-1)if radius_accumulator[score_i] < score_threhold:iscenter = Falseif iscenter:centers[0].append(sort_centers[i][0]/center_axis_scale)centers[1].append(sort_centers[i][1]/center_axis_scale)centers[2].append(score_i/radius_scale)centers = np.array(centers)centers = centers.astype(np.float64)return centers