一、原理
队列通常是链表结构,只允许在一端进行数据插入,在另一端进行数据删除。
队列的特性是链式存储(随机增删)和先进先出(FIFO:First In First Out)。
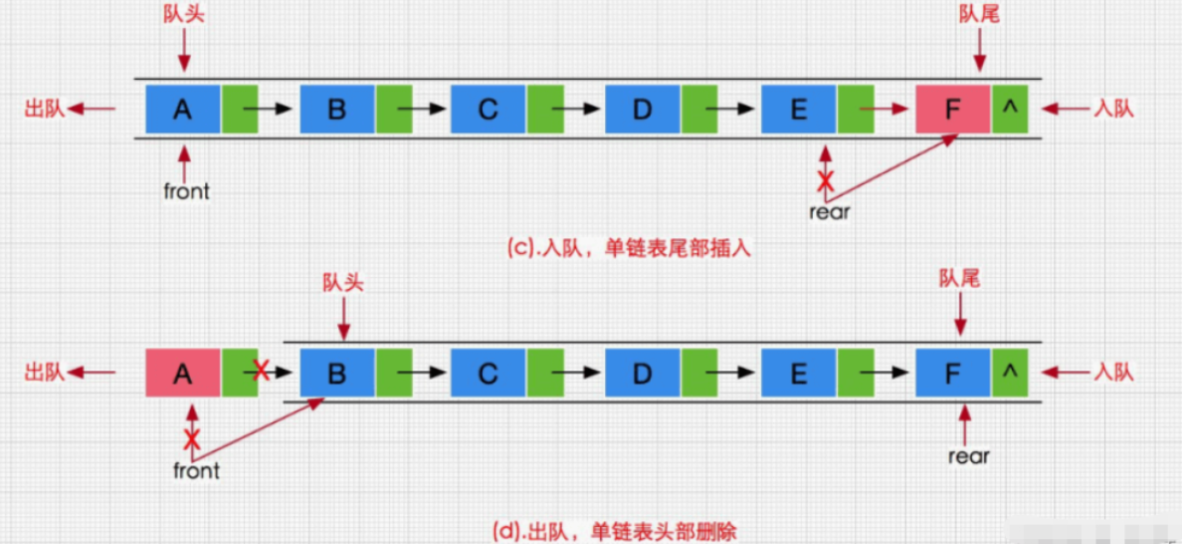
队列的缺陷:
- 不支持随机访问
- 不支持随机增删
- 每个数据都需要维护一个指针,增大了空间资源消耗
二、Queue.h
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
#include <stdlib.h>typedef int DataType;typedef struct Node
{DataType data;struct Node* next;
}Node;typedef struct Queue
{Node* head;int size;
}Queue;void Init(Queue* q)
{// 初始化创建一个空的头节点q->head = (Node*)malloc(sizeof(Node));q->head->next = NULL;q->size = 0;
}int Empty(Queue* q)
{return q->size == 0;
}void Push(Queue* q, DataType x)
{Node* node = (Node*)malloc(sizeof(Node));node->data = x;node->next = NULL;Node* cur = q->head;while (cur->next != NULL){cur = cur->next;}cur->next = node;++q->size;
}void Pop(Queue* q)
{if (Empty(q)){printf("队列为空,pop失败\n");return;}Node* cur = q->head->next;q->head->next = cur->next;free(cur);cur = NULL;--q->size;
}DataType Front(Queue* q)
{if (Empty(q)){printf("队列为空,无队列首元素\n");return NULL;}return q->head->next->data;
}void Destroy(Queue* q)
{while (!Empty(q)){Pop(q);}free(q->head);q->head = NULL;printf("队列销毁成功\n");
}int Size(Queue* q)
{return q->size;
}void Print(Queue* q)
{if (Empty(q)){printf("队列为空\n");return;}Node* cur = q->head->next;while (cur != NULL){printf("%2d ", cur->data);cur = cur->next;}printf(",队列首元素:%2d,队列长度为:%d\n", Front(q), Size(q));
}
三、test.c
#define _CRT_SECURE_NO_WARNINGS 1#include "Queue.h"int main()
{Queue q;Init(&q);Push(&q, 1);Push(&q, 3);Push(&q, 5);Push(&q, 7);Push(&q, 2);Push(&q, 4);Push(&q, 6);Push(&q, 8);Print(&q);Pop(&q);Pop(&q);Pop(&q);Print(&q);Push(&q, 9);Print(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Pop(&q);Print(&q);Push(&q, 10);Push(&q, 20);Print(&q);Destroy(&q);Print(&q);
}