文章目录
- 前言
- 双因子方差分析
- 数学模型
- 主效应分析
- 交互效应分析
- 正态性检验
- 绘制3个品种产量数据合并后的正态Q-Q图(数据:example8_2)
- 练习
前言
本篇将继续介绍方差分析的知识。
双因子方差分析
考虑两个类别自变量对数值因变量影响的方差分析称为双因子方差分析(two-way analysis of variance)(分析两个因子(因子A和因子B)对实验结果的影响) 分析时有两种情形:
只考虑两个因子对因变量的单独影响,即主效应(main effect)(如果两个因子对实验结果的影响是相互独立的,分别判断因子A和因子B对实验数据的单独影响),这时的双因子方差分析称为只考虑主效应的双因子方差分析或无重复双因子方差分析(Two-factor without replication)
除了两个因子的主效应外,还考虑两个因子的搭配对因变量产生的交互效应(interaction effect)(如果除了因子A和因子B对实验数据的单独影响外,两个因子的搭配还会对结果产生一种新的影响),这时的双因子方差分析称为考虑交互效应的双因子方差分析或可重复双因子方差分析 (Two-factor with replication)
数学模型
如果只考虑主效应而不考虑交互效应,两个因子的每种组合可以只测得一个观察值,即K=1。但要考虑交互效应时,每种组合就必须重复测量多个观察值,一般要求每种处理的重复次数K不小于2。
为便于表述,我们引进下列记号:



就是只考虑主效应时双因子方差分析的数学模型,显然它是考虑交互效应的方差分析模型的一个特例。

主效应分析
效应检验:
提出假设
对于因子A的I个处理和因子B的J个处理,要检验因子A和因子B对因变量的影响效应,也就是检验下面的假设:
检验因子A的假设:
𝐻_0:𝛼_𝑖=0(𝑖=1,2,⋯,𝐼)(因子A的处理效应不显著)
𝐻_1:𝛼_𝑖至少有一个不等于0 (因子A的处理效应显著)
检验因子B的假设:
𝐻_0:𝛽_𝑗=0(𝑗=1,2,⋯,𝐽)(因子B的处理效应不显著)
𝐻_1:𝛽_𝑗至少有一个不等于0 (因子B的处理效应显著)
各因子的效应用误差来表示。检验上述假设时,与线性模型对应的误差分解过程如下图所示:
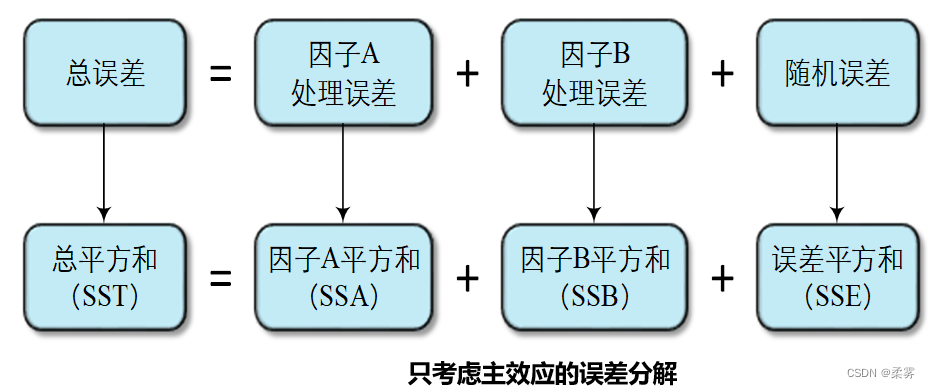

将各平方和(SS)除以相应的自由度df,得到各均方(MS),再将各处理均方(MSA和MSB)分别除以误差均方(MSE),即得到用于检验因子A和因子B主效应的统计量FA和FB。只考虑主效应的双因子方差分析表如下表所示:

如果两个因子的每种处理组合只测得一个观察值,即k=1,则误差平方和SSE的自由度为:df=IJ-I-J+1=(I-1)(J-1)。
总平方和SST的自由度为IJ-1。
例题:
(数据:example8_5.Rdata)假定在例8-1中,除了考虑品种对产量的影响外,还考虑施肥方式对产量的影响。假定有甲、乙两种施肥方式,这样3个小麦品种和两种施肥方式的搭配共有3×2=6种组合。如果选择30个地块进行实验,每一种搭配可以做5次实验,也就是每个品种(处理)的样本量为5,即相当于每个品种(处理)重复做了5次实验。实验取得的数据如下表所示。检验小麦品种和施肥方式对产量的影响是否显著(a=0.05)
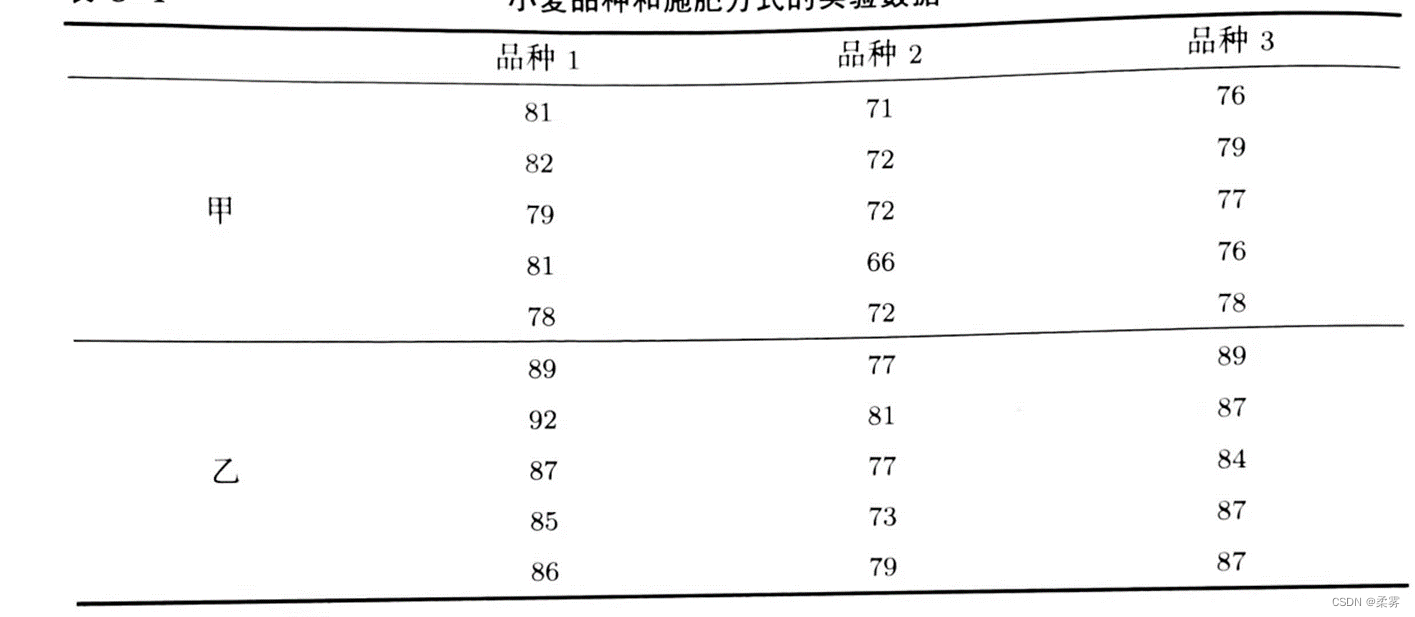
解:设品种(因子A)对产量的附加效应分别为α1(品种1)、α2(品种2)和α3(品种3);施肥方式(因子B)对产量的附加效应分别为β1(施肥方式甲)、β2(施肥方式乙)。
检验品种效应的假设为:
H0:α1=α2=α3=0(品种对产量的影响不显著)
H1:α1,α2,α3至少有一个不等于0(品种对产量的影响显著)
检验施肥方式效应的假设为:
H0:β1=β2=0(施肥方式对产量的影响不显著)
H1:β1,β2至少有一个不等于0(施肥方式对产量的影响显著)
首先,绘制按不同品种和不同施肥方式分组的箱线图,并计算按品种和施肥方式交叉分类的均值和标准差,描述品种和施肥方式对产量的影响。R代码和结果如下所示:
# 加载数据,将表8-4的短格式数据(table8_4)转为长格式数据,并另存为example8_5table8_4<-read.csv("c:/example/ch8/table8_4.csv")
table8_4<-cbind(table8_4,id=c(factor(1:10)))
table8_4library(reshape)
example8_5<-melt(table8_4,id.vars=c("id","施肥方式"))
example8_5<-rename(example8_5,c(variable="品种",value="产量"))save(example8_5,file="C:/example/ch8/example8_5.RData")
load("C:/example/ch8/example8_5.RData")
example8_5
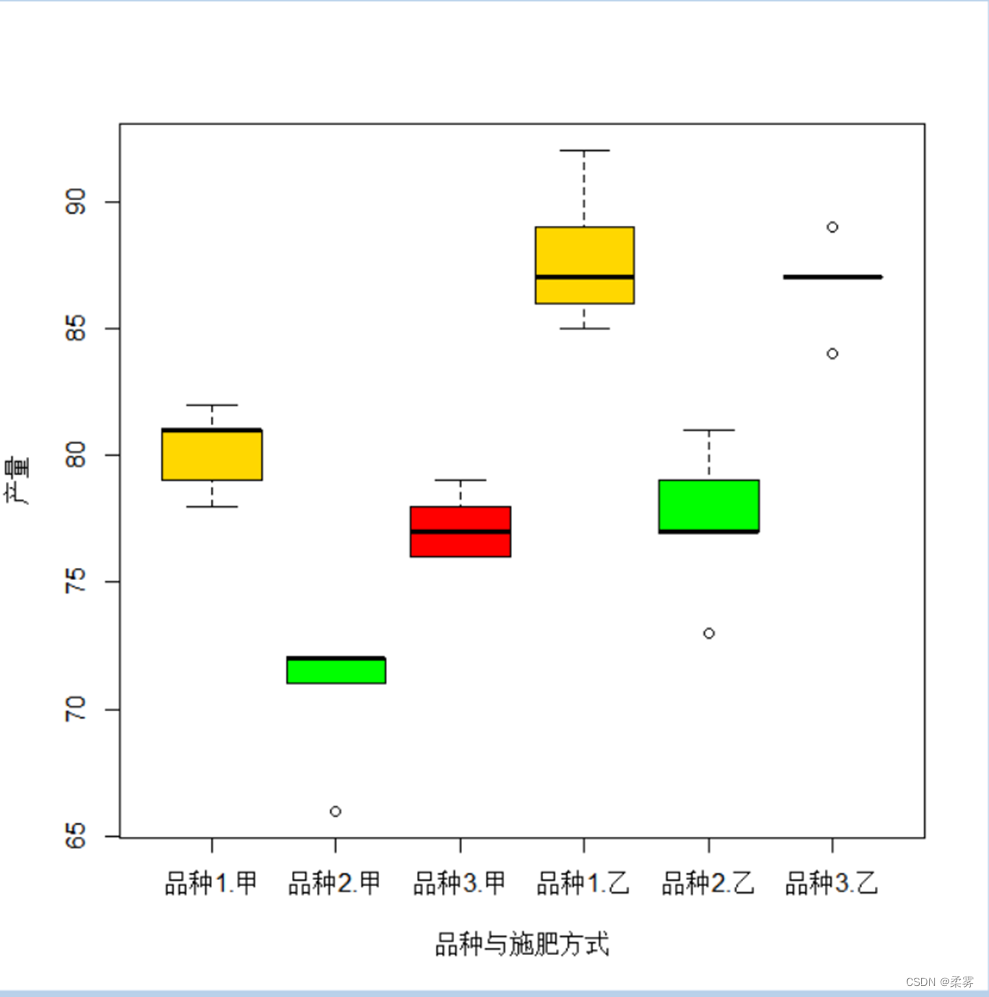
# 绘制品种和施肥方式的箱线图attach(example8_5)
boxplot(产量~品种+施肥方式,col=c("gold","green","red"),ylab="产量",xlab="品种与施肥方式",data=example8_5)
# 按品种和施肥方式交叉分类计算均值和标准差library(reshape)
library(agricolae)
mystats<-function(x)(c(n=length(x),mean=mean(x),sd=sd(x)))
dfm<-melt(example8_5,measure.vars="产量",id.vars=c("品种","施肥方式"))
cast(dfm,品种+施肥方式+variable~.,mystats)
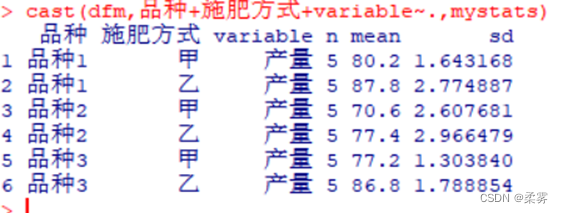
从图中可以看出,无论采用哪种施肥方式,品种2的产量都较低,品种1和品种3的产量差异不大;
施肥方式甲的产量比施肥方式乙低。从分组计算的均值也可以得到与箱线图相同的结论。但它们对产量的影响是否显著还需要进一步做方差分析。R代码和结果如下所示:
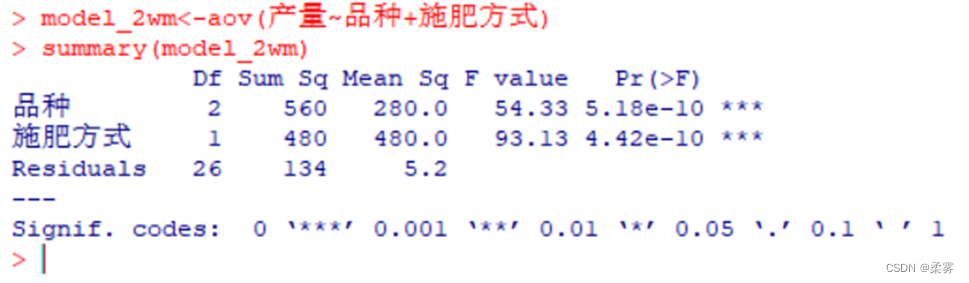
# 主效应方差分析结果model_2wm<-aov(产量~品种+施肥方式)
summary(model_2wm)
# 主效应方差分析模型的参数估计model_2wm$coefficients

由方差分析表可知,检验品种和施肥方式两个因子的P值(Pr(>F))均接近于0,表示两个因子对产量均有显著影响。
上图中的截距(Intercept)是模型 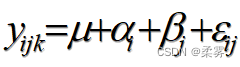 中的常数项μ,它表示不考虑品种和施肥方式影响时产量的均值为80kg。接下来是对品种的影响效应
中的常数项μ,它表示不考虑品种和施肥方式影响时产量的均值为80kg。接下来是对品种的影响效应 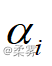 和施肥方式的影响效应
和施肥方式的影响效应 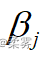 的估计。由于3个品种共有3个参数,在估计模型的参数时,将第一个水平(本例为品种1)作为参照水平,这相当于强迫α1=0,而另外两个参数(品种2和品种3)的估计值实际上就是与参照水平相比较的结果。比如,品种2的参数α2=-10,表示品种2对产量的附加效应;施肥方式的参数β1=8,表示施肥方式为乙时对产量的附加效应(施肥方式甲作为参照水平)等等。
的估计。由于3个品种共有3个参数,在估计模型的参数时,将第一个水平(本例为品种1)作为参照水平,这相当于强迫α1=0,而另外两个参数(品种2和品种3)的估计值实际上就是与参照水平相比较的结果。比如,品种2的参数α2=-10,表示品种2对产量的附加效应;施肥方式的参数β1=8,表示施肥方式为乙时对产量的附加效应(施肥方式甲作为参照水平)等等。
交互效应分析
1、效应检验:
如果除了考虑品种和施肥方式两个因子的主效应外,还考虑两个因子搭配对产量的交互作用,则方差分析的模型为:
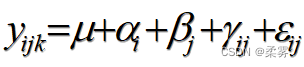
对于因子A的I个处理和因子B的J个处理,要检验因子A的效应、因子B的效应、两个因子的交互效应,也就是检验如下假设:
检验因子A的假设:
𝐻_0:𝛼_𝑖=0(𝑖=1,2,⋯,𝐼)(因子A的处理效应不显著)
𝐻_1:𝛼_𝑖至少有一个不等于0 (因子A的处理效应显著)
检验因子B的假设:
𝐻_0:𝛽_𝑗=0(𝑗=1,2,⋯,𝐽)(因子B的处理效应不显著)
𝐻_1:𝛽_𝑗至少有一个不等于0 (因子B的处理效应显著)
检验交互效应的假设:
𝐻_0:𝛾_𝑖𝑗=0(交互效应不显著)
𝐻_1:𝛾_𝑖𝑗至少有一个不等于0(交互效应显著)
1、效应检验:
检验上述假设时,与方差分析模型对应的总误差分解过程可用下面的图表示
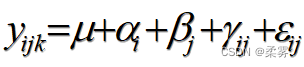
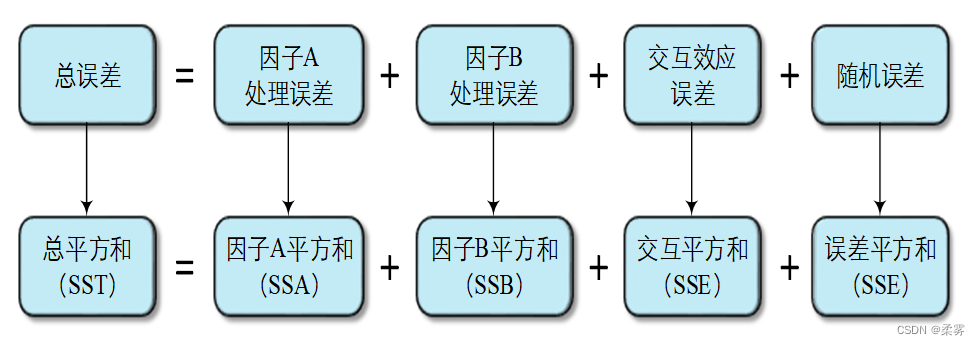
根据上述误差分解原理,可以构建用于检验的统计量FA,FB,FAB。其原理与只考虑主效应的双因子方差分析类似,其方差分析表如下表所示:
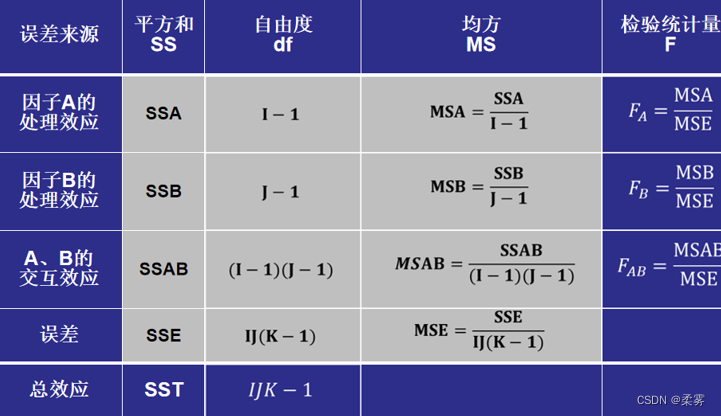
例题:
(数据: example8_5. RData)沿用8-5。检验品种、施肥方式及其交互效应对产量的影响是否显著(α=0.05)
解:设品种对产量的附加效应分别为α1(种1)、α2(品种2)和α3(品种3);施肥方式对产量的附加效应分别为β1(方式甲)、β2(方式乙);交互效应为
检验品种效应的假设为:
H0:α1=α2=α3=0(品种对产量的影响不显著)
H1:α1,α2,α3至少有一个不等于0(品种对产量的影响显著)
检验施肥方式效应的假设为:
H0:β1=β2=0(施肥方式对产量的影响不显著)
H1:β1,β2至少有一个不等于0(施肥方式对产量的影响显著)

# 交互效应方差分析表attach(example8_5)
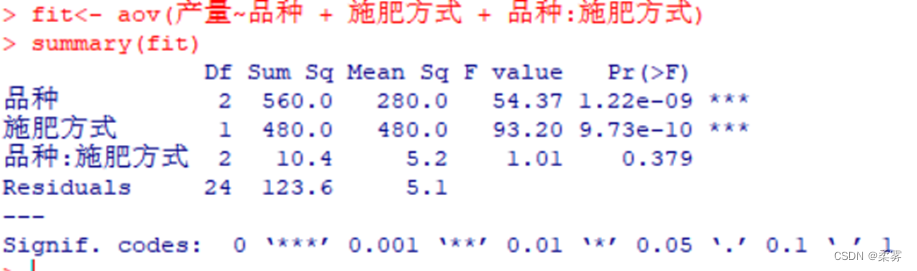
fit<- aov(产量~品种 + 施肥方式 + 品种:施肥方式)
summary(fit)
# 交互效应方差分析模型的参数估计fit$coefficients

方差分析表显示,检验品种和施肥方式的P均小于0.05,表示两个因子对产量的影响均显著,而检验交互效应的P=0.379,大于0.05,表示交互效应对产量的影响不显著。
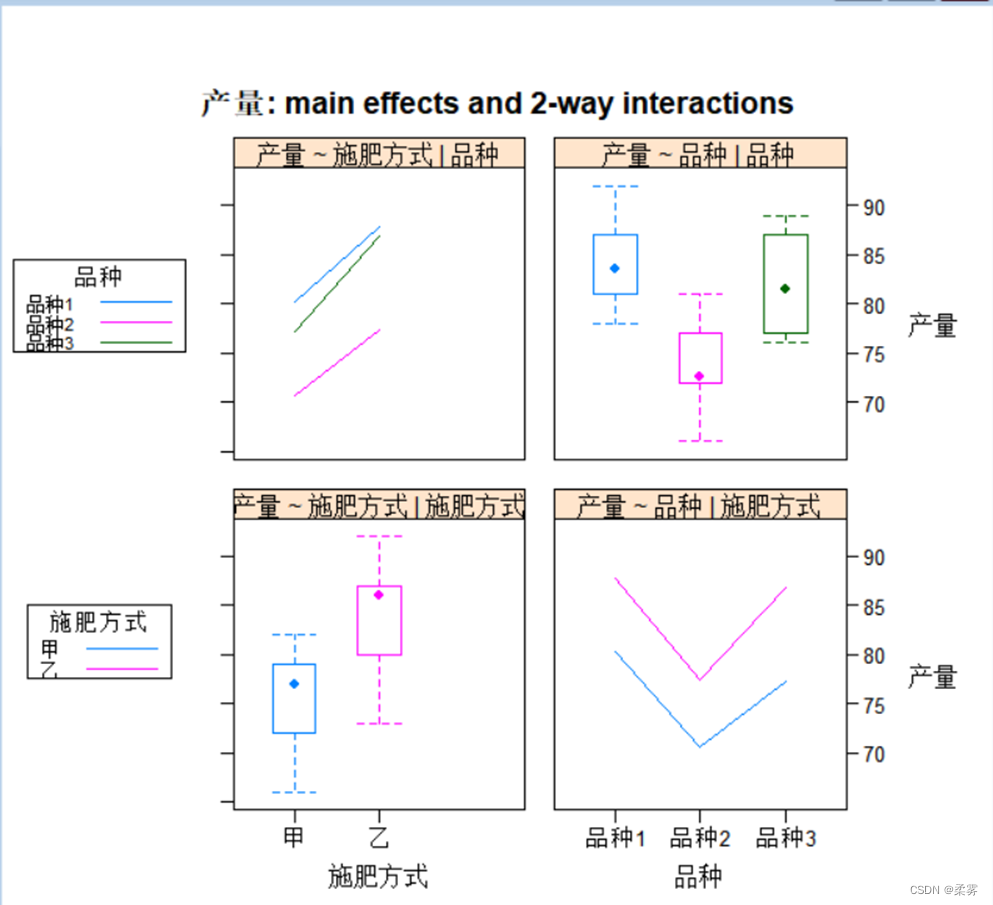
# 绘制品种和施肥方式的主效应和交互效应图library(HH)
interaction2wt(产量~施肥方式+品种,data=example8_5)
注:函数 interaction2wt(x,…)用于绘制多因子设计的主效应和交互效应,x为方差分析的对象
图中的箱线图反映了每个因子的主效应,可观察品种和施肥方式对产量是否有影响;
折线图反映了两个因子的交互效应。由于图中的各条折线基本上是平行的表示两个因子间无明显的交互效应(无交互效应时,一个因子各处理间均值的差异不会随另一个因子处理的变化而变化,各条折线是平行的。如果各条线明显不平行或之间有交叉,则意味着两个因子的各处理间存在交互效应)。
为比较主效应方差分析模型和交互效应方差分析模型是否有显著差异,可采用R中的 anova函数比较两个模型。比较主效应模型( model_2wm)和交互效应模型( model_2vi)的R代码和结果如下所示:
model_2wm<-lm(产量~品种+施肥方式,data=example8_5)
model_2wi<-lm(产量~品种+施肥方式+品种:施肥方式,data=example8_5)
anova(model_2wm,model_2wi)

注:函数anova(object,…)用于计算方差分析表。用 anova比较模型时,一个模型必须包含在另一个模型中,也就是说,较小的模型中的所有项必须出现在较大的模型中。比如在本例中, Model1:产量品种+施肥方式,Mode2:产量品种+施肥方式+品种:施肥方式。Model1中的所有项 都包含在Model2中。
该检验的原假设是两个模型无显著差异。图中显示了两个模型的残差平方和(RSS)、交互效应平方和(Sum of Sq)、检验统计量(F)及其相应的P值。由于P=0.3793,不拒绝原假设,没有证据显示两个模型有显著差异,这也从另一个角度佐证了交互效应不显著。从简化分析的角度看,就本例而言,采用主效应模型比较合适。
需要注意的是,有两个实验因子时,考虑交互效应的方差分析与分别对两个因子做单因子方差分析是不同的。对两个因子分别做单因子方差分析实际上是假定两个因子间不存在交互效应,当两个因子间存在交互效应时可能会得出错误结论。因此,当有两个因子时,应首先考虑使用交互效应方差分析模型,当交互效应不显著时,再考虑使用主效应方差分析模型,或者考虑使用两个因子的单因子方差分析模型。
正态性检验
方差分析的基本假定:
在方差分析模型中,假定误差项是期望值为0、方差相等的正态独立随机变量,在做方差分析之前,应首先对这些假定进行检验,考察数据是否适合做方差分析。
正态性(normality)。每个总体都应服从正态分布,即对于因子的每一个水平,其观测值是来自正态分布总体的简单随机样本
在例8-1中,要求每个品种的产量必须服从正态分布
检验总体是否服从正态分布的方法有很多,包括对样本数据作直方图、茎叶图、箱线图、正态概率图做描述性判断,也可以进行非参数检验等
正态性检验(图示法)
绘制因变量的正态概率图
当每个处理的样本量足够大时,可以对每个样本绘制正态概率图来检查每个处理对应的总体是否服从正态分布
当每个处理的样本量比较小时,正态概率图中的点很少,提供的正态性信息很有限。这时,可以将每个处理的样本数据合并绘制一个正态概率图来检验正态性
例:沿用例8-2。分别用Q-Q图和检验方法,检验各品种小麦产量是否服从正态分布(α=0.05)
解:首先,绘制Q-Q图来检验小麦产量是否服从正态分布。当每个处理的样本量足够大时,可以对每个样本绘制Q-Q图来检查每个处理对应的总体是否服从正态分布。但是,当每个处理的样本量比较小时,正态概率图中的点很少,提供的正态性信息有限。这时,可以将每个处理的样本数据合并绘制一幅正态概率图来检验正态性。R代码和结果如下所示
load("C:/example/ch8/example8_1.RData")
par(mfrow=c(1,3))
qqnorm(example8_1$品种1,xlab="期望正态值",ylab="观察值",datax=TRUE,main="品种1的Q-Q图")
qqline(example8_1$品种1,datax=TRUE)
qqnorm(example8_1$品种2,xlab="期望正态值",ylab="观察值",datax=TRUE,main="品种2的Q-Q图")
qqline(example8_1$品种2,datax=TRUE)
qqnorm(example8_1$品种3,xlab="期望正态值",ylab="观察值",datax=TRUE,main="品种3的Q-Q图")
qqline(example8_1$品种3,datax=TRUE)
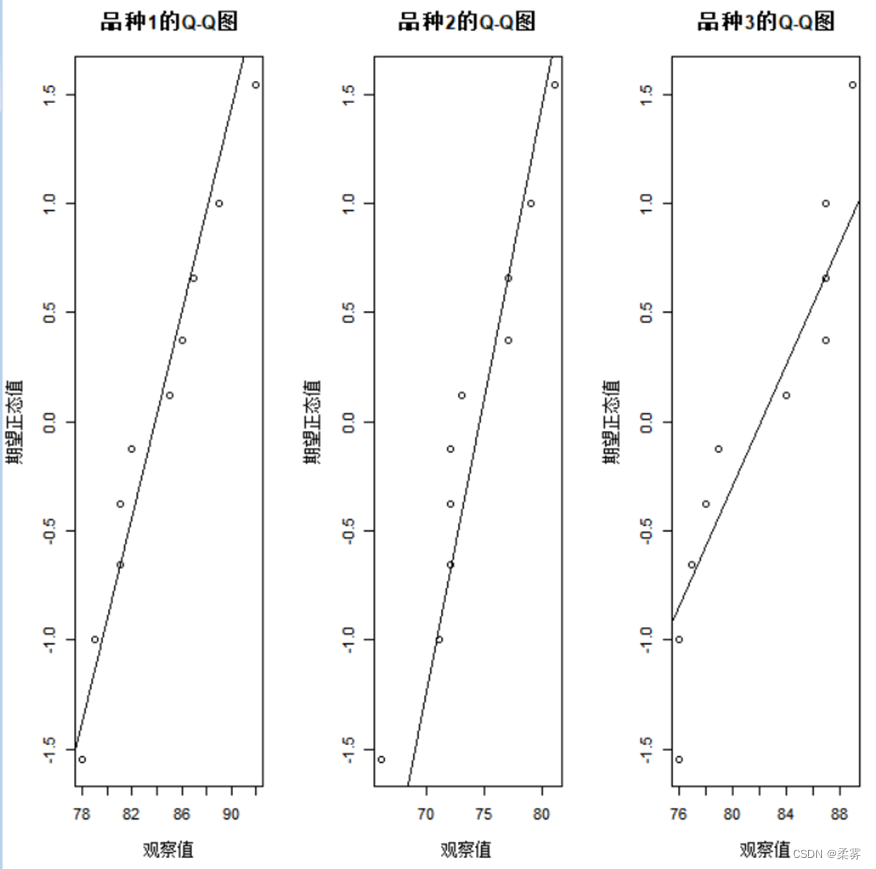
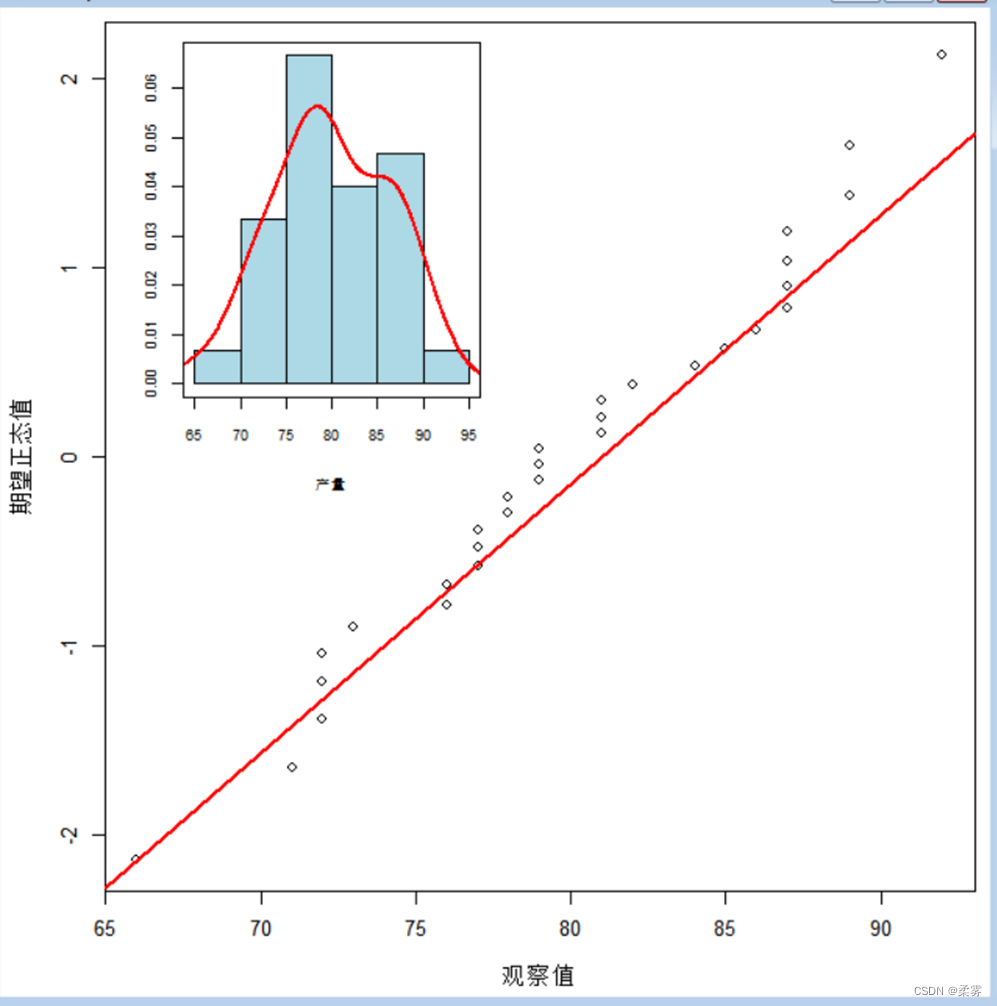
由于图中对每个品种绘制的正态概率图只有10个数据点,很难提供正态性的证据。但从3个品种的产量数据合并后绘制的Q-Q图(下页图)可以看出,产量基本上服从正态分布。
其次,分别采用 Shapiro-Wilk检验和KS检验来判断产量是否服从正态分布。R代码和结果如下所示
绘制3个品种产量数据合并后的正态Q-Q图(数据:example8_2)
load("C:/example/ch8/example8_2.RData")
par(cex=.8,mai=c(.7,.7,.1,.1))
qqnorm(example8_2$产量,xlab="期望正态值",ylab="观察值",data=TRUE,main="")
qqline(example8_2$产量,datax=TRUE,col="red",lwd=2)
op<-par(fig=c(.08,.5,.5,.98),new=TRUE)
hist(example8_2$产量,xlab="产量",ylab="",freq=FALSE,col="lightblue", cex.axis=0.7,cex.lab=0.7,main="")
lines(density(example8_2$产量),col="red",lwd=2)
box()
正态性检验(检验法)
当样本量较小时,正态概率图的应用就会受到很大限制,这时可以使用标准的统计检验
如Shapiro-Wilk检验、Kolmogorov-Smirnov检验等,均可以做正态性检验。这些检验的原假设是因变量服从正态分布
如果检验获得的P值小于指定的显著性水平,则拒绝原假设,表明总体不服从正态分布,如果P值较大不能拒绝原假设时,可以认为总体满足正态分布
这些检验对正态性的轻微偏离是敏感的,检验往往导致拒绝原假设。而方差分析对正态性的要求则相对比较宽松,当正态性略微不满足时,对分析结果的影响不是很大。因此,实际中应谨慎使用这些检验。
##每个品种产量的正态性检验
# 品种1 的正态性检验:load("C:/example/ch8/example8_2.RData")attach(example8_2)shapiro.test(产量[品种=='品种1'])ks.test(产量[品种=='品种1'],"pnorm",mean(产量[品种=='品种1']),sd(产量[品种=='品种1']))

##每个品种产量的正态性检验
# 品种2 的正态性检验:shapiro.test(产量[品种=='品种2'])
ks.test(产量[品种=='品种2'],"pnorm",mean(产量[品种=='品种2']),sd(产量[品种=='品种2']))

##每个品种产量的正态性检验
# 品种3 的正态性检验:shapiro.test(产量[品种=='品种3'])
ks.test(产量[品种=='品种3'],"pnorm",mean(产量[品种=='品种3']),sd(产量[品种=='品种3']))

##三个品种产量数据合并后的检验
# shapiro正态性检验load("C:/example/ch8/example8_2.RData")
attach(example8_2)
shapiro.test(产量)

# K-S正态性检验ks.test(产量,"pnorm",mean(产量),sd(产量))

##双因子方差分析:Shapiro-Wilk正态性检验和k-s检验(数据:example8_5)
# 施肥方式甲 的产量正态性检验:load("C:/example/ch8/example8_5.RData")
attach(example8_5)
shapiro.test(产量[施肥方式=='甲'])
ks.test(产量[施肥方式=='甲'],"pnorm",mean(产量[施肥方式=='甲']),sd(产量[施肥方式=='甲']))

##双因子方差分析:Shapiro-Wilk正态性检验和k-s检验(数据:example8_5)
# 施肥方式乙的产量正态性检验:shapiro.test(产量[施肥方式=='乙'])
ks.test(产量[施肥方式=='乙'],"pnorm",mean(产量[施肥方式=='乙']),sd(产量[施肥方式=='乙']))

上述两种检验方法几乎P>0.05,不拒绝H0,可以认为产量服从正态分布。
练习
1、一家牛奶公司有4台机器装填牛奶,每桶的容量为4L。下面是从4台机器中抽取的装填量样本数据。
检验装填量是否满足正态性质?
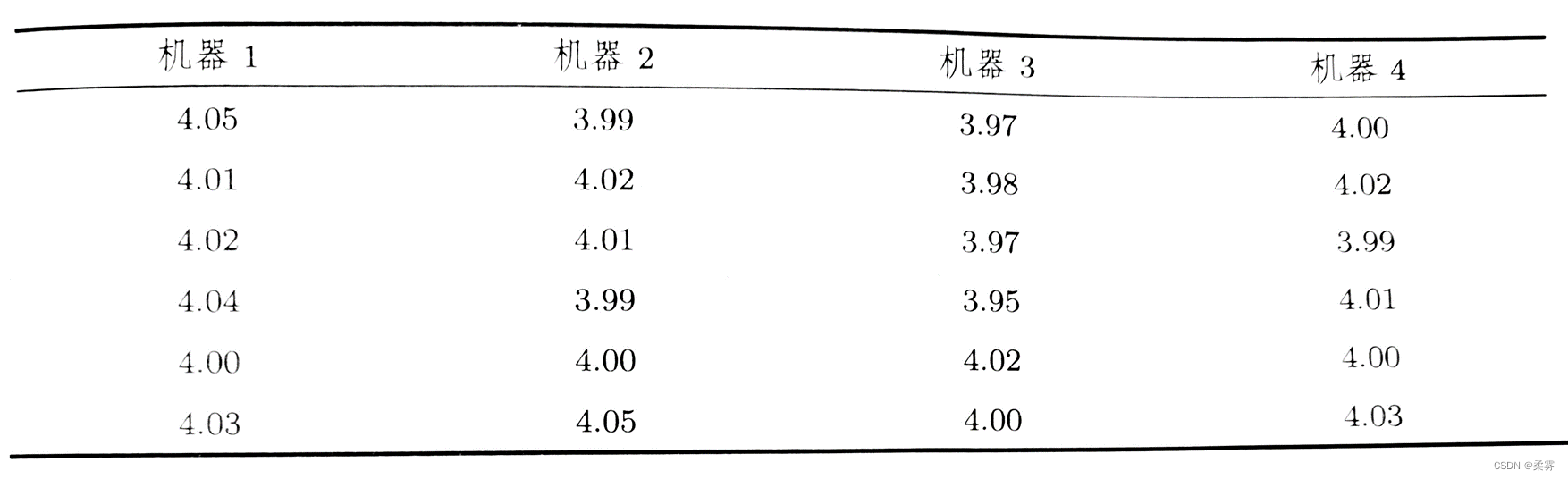
解:提出假设:
H0: 机器对装填量的影响不显著
H1:机器对装填量的影响显著
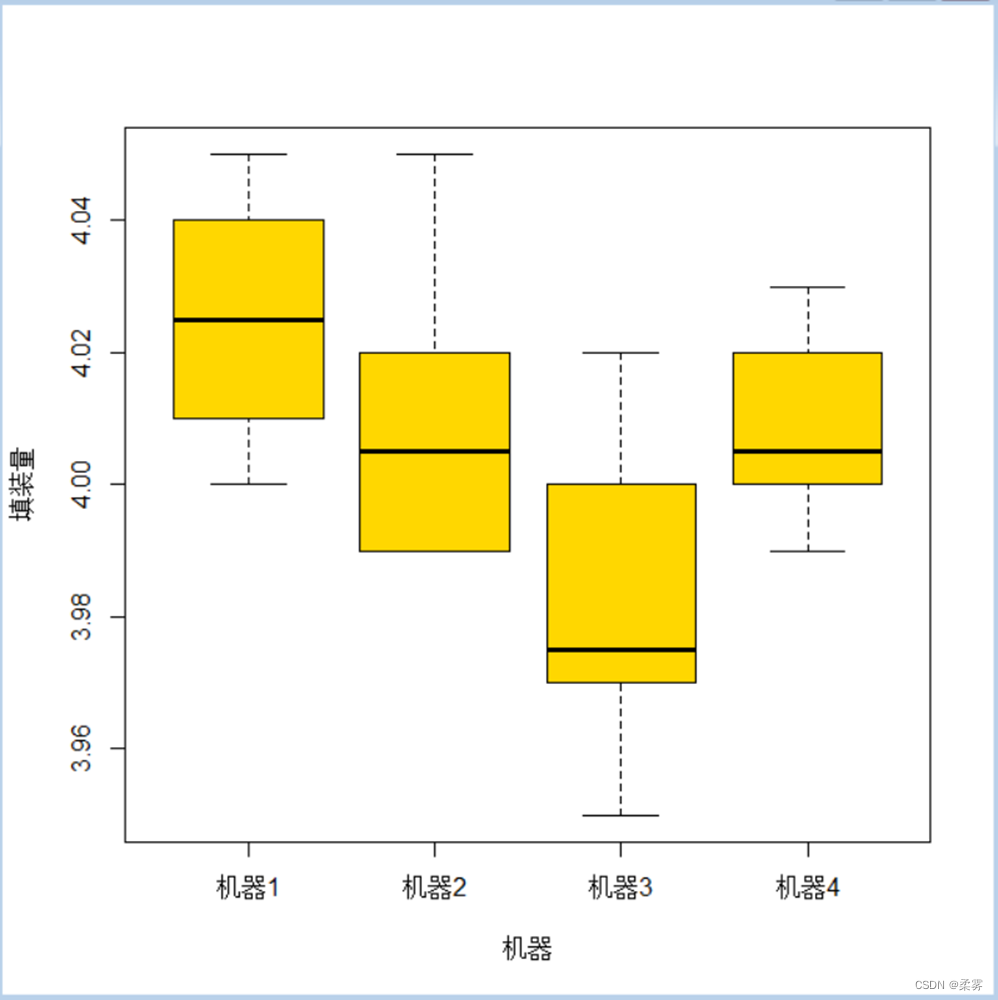
#绘制出箱线图load("C:/example/ch8/exercise8_1.RData")
exercise8_1
attach(exercise8_1)
boxplot(填装量~机器,data=exercise8_1,col="gold",main="",ylab="填装量", xlab="机器")
# 方差分析表attach(example8_2)
model_1w<-aov(填装量~机器)
summary(model_1w)
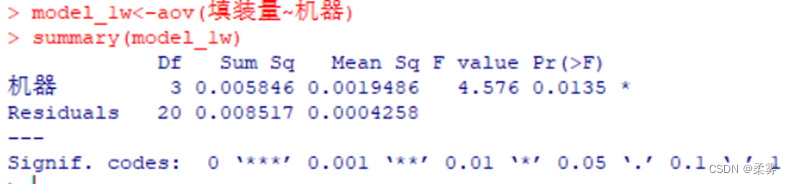
方差分析表显示了机器效应和随机效应的平方和(Sum Sq)、自由度(Df)、均方(Mean Sq)、检验统计量值(F value)、检验的P值(Pr(>F))。由于P=0.0135<0.05,拒绝原假设,机器对填装量的影响效应显著。
# 方差分析模型的参数估计model_1w$coefficients

2、(exercise8_4)有5个不同品种的种子和4个不同的施肥方案,在20块同样面积的土地上分别采用5种种子和4个施肥方案搭配进行实验,取得的产量数据如下:
检验不同品种和施肥方案对产量的影响是否显著(α=0.05)
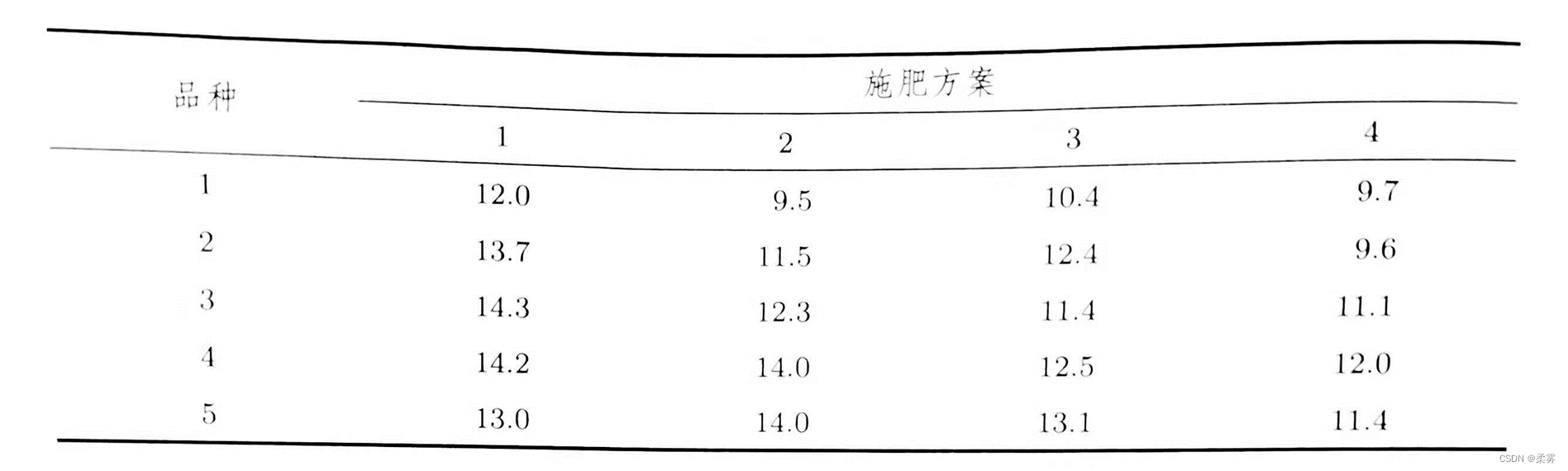
解:
检验路段效应的假设为:
H0:α1=α2=α3=0(路段对行车时间的影响不显著)
H1:α1,α2,α3至少有一个不等于0(路段对行车时间的影响显著)
检验时段效应的假设为:
H0:β1=β2=0(时段对行车时间的影响不显著)
H1:β1,β2至少有一个不等于0(时段对行车时间的影响显著)

load("C:/example/ch8/exercise8_5.RData")
exercise8_5
# 交互效应方差分析表
attach(exercise8_5)
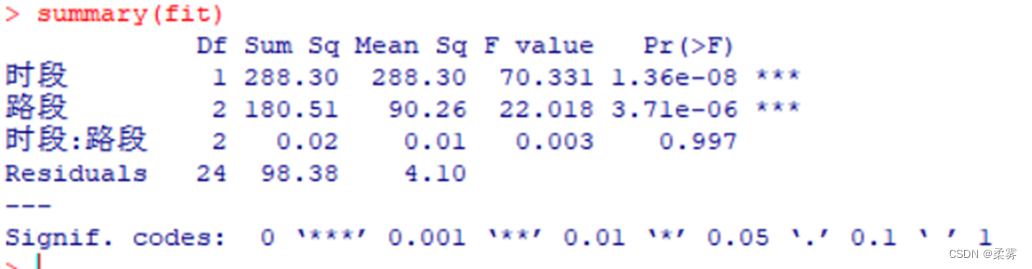
fit<- aov(行车时间~时段 + 路段 + 时段:路段)
summary(fit)
方差分析表显示,检验时段和路段的P值均小于0.05,表示两个因子对行车时间的影响均显著,而检验交互效应的P=0.997,大于0.05,表示交互效应对行车时间的影响不显著。