题目1：738 单调递增的数字

题目链接：738 单调递增的数字

题意

每个相邻位的数字的前一位小于等于后一位，则该整数是单调递增的

返回小于或等于n的最大数字且单调递增

代码

class Solution {
public:int monotoneIncreasingDigits(int n) {//转化为字符串string str = to_string(n);int flag = str.size();//从后向前遍历for(int i=str.size()-1;i>0;i--){//非递增if(str[i]<str[i-1]){str[i-1]--;flag = i;}}for(int i=flag;i<str.size();i++) str[i] = '9';return stoi(str);//转化为整数}
};

• 时间复杂度：O(n)，n 为数字长度
• 空间复杂度：O(n)，需要一个字符串，转化为字符串操作更方便

题目2：968 监控二叉树

题目链接：968 监控二叉树

题意

在二叉树的节点上安装摄像头，节点的摄像头可以监视其父节点，自身已经左右孩子

如果监控所有节点，最少需要多少个摄像头

注意

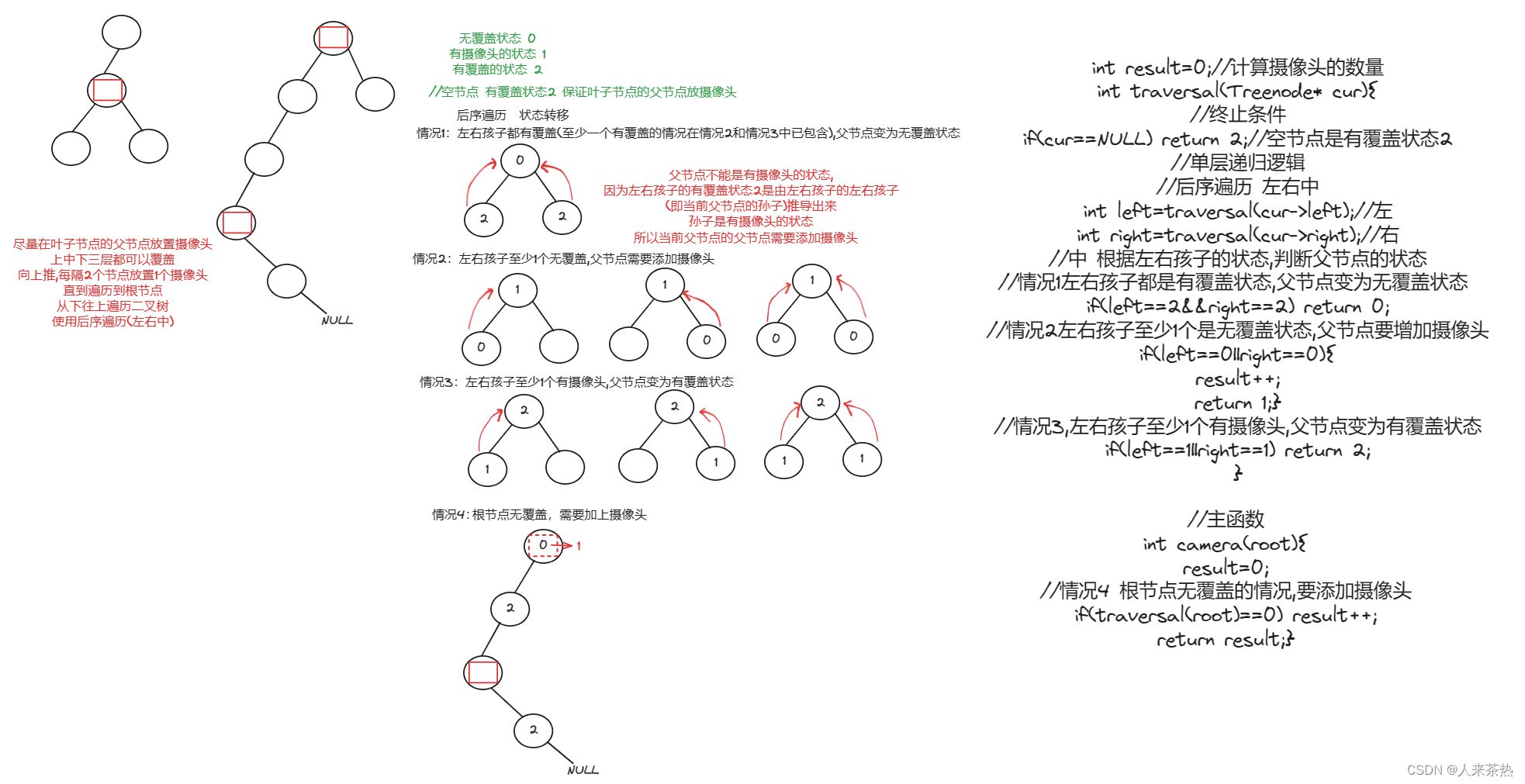
1）添加节点在叶子节点的父节点添加，这样可以使用少量的摄像头，每隔两个节点添加摄像头

2）遍历顺序 后序遍历

3）3种状态的转移  无覆盖状态0 有摄像头状态1 有覆盖状态2 

4）空节点是有覆盖状态   

5）根节点是无覆盖状态时 要添加一个摄像头

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int result = 0;int traversal(TreeNode* cur){//终止条件  空节点是有覆盖状态2if(cur==NULL) return 2;//单层递归逻辑//后序遍历  左右中//左int left = traversal(cur->left);//右int right = traversal(cur->right);//中//情况1 左右孩子均为有覆盖状态2 父节点需为无覆盖状态0if(left==2 && right==2) return 0;//情况2 左右孩子至少一个无覆盖状态0 父节点需要添加摄像头if(left==0 || right==0){result++;return 1;}//情况3 左右孩子至少一个有摄像头1 父节点需为有覆盖状态if(left==1 || right==1) return 2;return -1;}int minCameraCover(TreeNode* root) {//情况4 根节点无覆盖状态 需添加摄像头if(traversal(root)==0) result++;return result;}
};

• 时间复杂度: O(n)，需要遍历二叉树上的每个节点
• 空间复杂度: O(n)