使用MATLAB拟合正态分布的主要步骤是:
- 输入样本数据
使用变量x保存样本数据,例如:
x = [1.2, 3.4, 2.1, 0.5, 4.3];
- 调用正态分布的最大似然估计函数
使用normfit函数来完成正态分布的参数的最大似然估计:
[mu_hat,sigma_hat] = normfit(x);
normfit函数会返回正态分布位置参数μ和标准差σ的最大似然估计值。
- 验证拟合结果
-
打印出估计得到的μ和σ值,观察是否与经验分布参数相符合
-
绘制样本数据的直方图与用μ,σ参数的正态概率密度函数曲线进行对比
-
计算K-S检验统计量,判断两者是否来自同一分布
例如:
f = @(x) normpdf(x,mu_hat,sigma_hat);
kstest(x,f)
- 使用拟合的正态分布
利用μ_hat和sigma_hat参数的正态分布来描述样本数据,或对新数据进行预测分析。
以上是使用MATLAB中内置函数normfit来拟合正态分布的主要步骤。normfit函数实现了最大似然估计原理,能快速和方便地对数据进行正态分布拟合。
数据如下:
adata =
7.05176091320878
3.0004827744495
13.6419303185884
13.4683302117893
9.68042864376785
13.5939039575086
10.734813692365
11.1631605395378
10.4517788680842
11.7598087554898
10.4066497748014
21.1493409112537
5.33333987922144
2.58280366924122
5.43727542132147
5.62662617504158
8.26556281410071
9.32612048689821
9.12586575989368
12.1653377428775
11.5570648153731
13.0049159387533
17.113023597164
14.8922502069352
4.86697558158093
0.684181934866633
13.6077258678069
2.65744526505923
10.2670276457475
10.1419179433503
18.9086723126715
9.72314298391181
7.97070774154201
10.943238690305
10.9832194075754
10.2801808376672
7.5656779596802
5.10962647925348
11.2660014431909
4.62852305351228
5.87126262371132
15.3248635402599
8.3243872198806
9.43871311177454
13.5992893155889
8.7995559775373
14.1174628484124
8.61973611373072
14.0512074570519
12.5173383397257
9.14793966943578
6.53721076655791
5.82756679464949
8.9197247494076
8.24743457759143
8.3653027408147
13.9341809408222
8.80921142396251
14.5747156430838
7.87351952997172
13.8902629120346
7.9109980600258
10.7063111785693
13.8829512942188
8.34411090010308
8.24691792718039
18.0135624434491
13.8039739981963
8.27198462508888
12.5957629494543
8.55969479538411
12.8235400773977
15.6633962737463
3.58193732561175
14.1154122760081
15.8318711226479
10.1898852930993
16.9850268404737
10.6215500568047
5.05152126134948
1.22602288466157
8.66637173094507
12.8541732102562
11.269630932938
11.6544415611725
7.69165766544824
10.5760072056179
3.44533708026445
6.95964000545893
6.72482761499897
12.0789155525345
9.94335976361118
5.37788252685104
9.96190033560734
7.24075784947316
7.33320338559534
13.4565976846605
10.4536777449075
11.593451384664
13.5358795609387
10.7210307759482
12.2034180882299
12.7318571044477
14.6824346401424
11.9034423491134
15.648930745778
10.0904339372384
9.80852235911918
16.8053386170998
7.96115314893029
9.98858015942272
13.6794683192256
10.599234930531
15.6197337827079
14.1364861582788
11.1662811550832
6.88920584675359
12.2667843901572
4.46951536207859
10.9778987023596
13.2337552126708
10.852166793668
13.518708656934
18.1555050056562
13.6957297947557
11.0676697863833
12.5666460256871
11.7019414225012
4.74110598605247
8.33435512120226
14.8987512991413
9.82566317781467
12.3296931097919
5.97399970152266
10.2580669692444
12.4011677967431
4.55394018054173
11.3903705278403
9.27262712616267
6.24186093623403
9.84986724472331
2.4147820255102
1.4880929272693
5.29230667714017
6.0378711180633
5.30787069093038
3.09828884188523
11.15291235866
3.62326511893277
10.4408753968935
13.1482667054319
9.99109285474466
10.3724350402352
8.48737177364097
4.06929555576399
9.82472565856682
13.8433008467285
16.9529797304534
8.2791750302956
3.49070905412088
10.6653899698403
11.5050636418029
9.09219814117507
5.40435084152484
18.0973303981755
0.561905956166035
7.96011181680024
4.71349763675959
7.45548700135983
11.2714056762388
10.5521918977981
7.1570597007551
13.1080141068792
12.4895756966881
12.5895235380642
8.29747327335859
14.1943230421458
12.6428283454687
20.0350898927404
14.2538385561641
14.6276866133096
10.2119153093025
4.84645598823883
8.51511501000947
6.96883233400473
7.74412433189029
12.2205542400074
7.77288774419854
6.41954745807026
8.36268911346372
9.35645293304623
11.6373377218218
6.18945601152009
11.2692698892984
10.3120803239123
15.2975417966409
9.14731805431366
9.46208542177829
5.31457672831882
4.45894926721904
代码如下:
clc;close all;clear all;warning off;%清除变量
format long g;
adata= normrnd(10,4,200,1)
[muhat,sigmahat] = normfit(adata);
x0=[1,1];
y=adata;
[parmhat1,ML]=fminsearch(@(x) mynpdffun(y,x),x0);
disp('最大似然估计得到的正态分布分布参数');
parmhat1
%% 画概率图
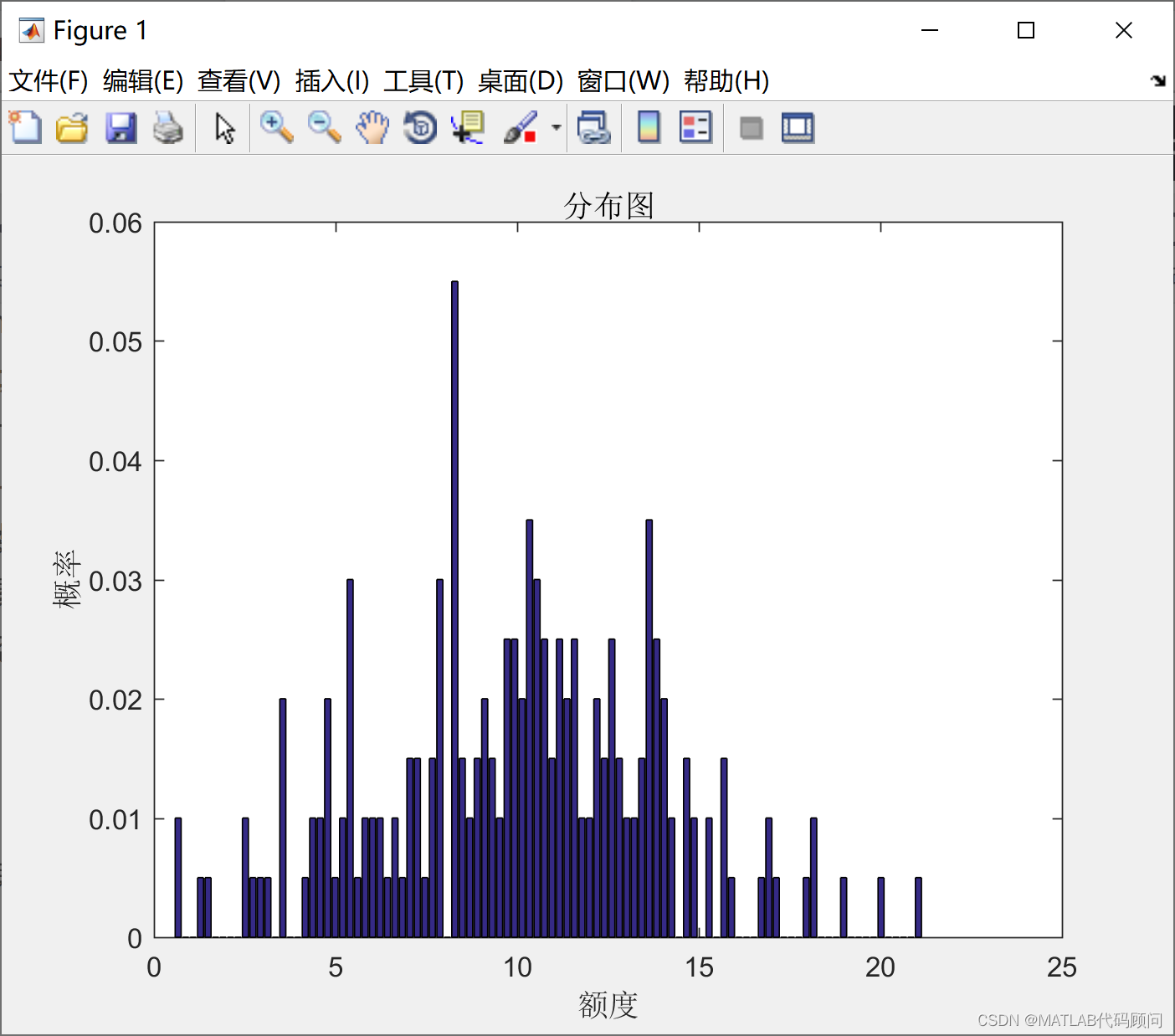
[counts,centers]=hist(y,100);
figure;
bar(centers,counts/sum(counts)); %画出概率密度分布图
xlabel('额度','fontname','宋体');
ylabel('概率','fontname','宋体');
title('分布图','fontname','宋体');
a1=normcdf(sort(y),parmhat1(1),parmhat1(2));
[counts,centers]=hist(y,100);
a0=counts/sum(counts);
g=cumsum(a0);
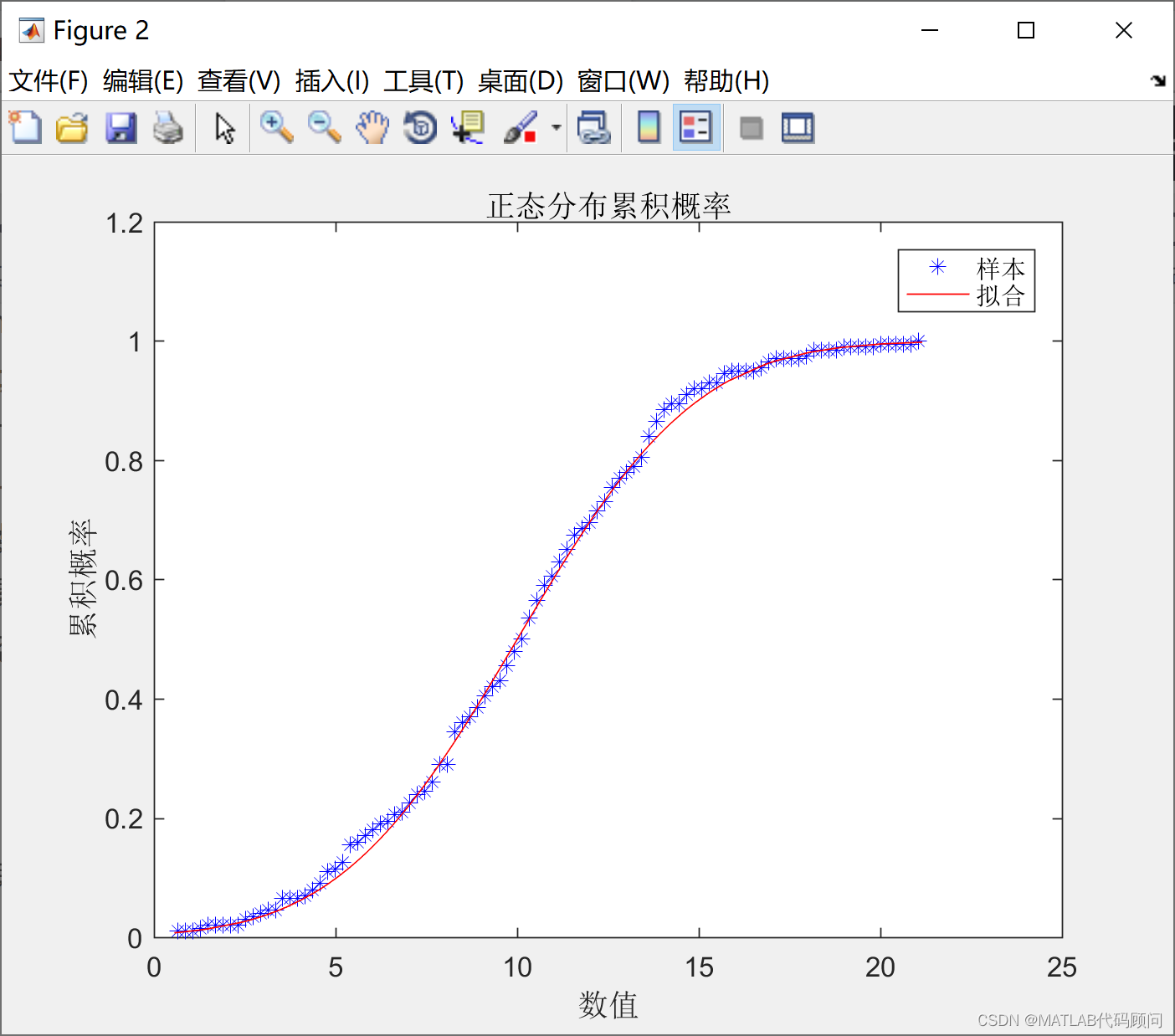
figure;
plot(centers,g,'b*'); %画出概率密度分布图
hold on;
plot(sort(y),a1,'r');
legend({'样本','拟合'},'fontname','宋体');
xlabel('数值','fontname','宋体');
ylabel('累积概率','fontname','宋体');
title('正态分布累积概率','fontname','宋体');
程序结果如下:
最大似然估计得到的正态分布分布参数
parmhat1 =
10.004444300048 3.87873606559659