重写Sylar基于协程的服务器（2、配置模块的设计）

重写Sylar基于协程的服务器（2、配置模块的设计）

重写Sylar基于协程的服务器系列：

重写Sylar基于协程的服务器（0、搭建开发环境以及项目框架 || 下载编译简化版Sylar）

重写Sylar基于协程的服务器（1、日志模块的架构）

重写Sylar基于协程的服务器（2、配置模块的设计）

重写Sylar基于协程的服务器（3、协程模块的设计）

重写Sylar基于协程的服务器（4、协程调度模块的设计）

重写Sylar基于协程的服务器（5、IO协程调度模块的设计）

配置模块存在的必要性

一个服务器软件可能会运行在不同的机器上，机器的配置、网络环境、实际需求等都是千变万化，在服务器软件中，为了适应这些变化，可能就是调整几个变量的值。开发人员不可能每次外在因素的改变就重新编译软件再发布，这明显是不现实的。于是配置模块就在这时发挥它的关键作用，利用好配置模块就不需要再次编译，让配置模块自己加载参数，动态调节就行了。

配置模块的设计与实现

配置模块序列化和反序列化效果（支持std::各种容器

YAML 的基本语法如下：

  1. 大小写敏感。

  2. 利用缩进表示层级关系，缩进只能使用空格，空格的数量不重要。

  3. '#'表示注释。

  4. 数据类型：对象，键值对的集合，即K-V对。数组，一组按次序排列的值。纯量（scalars），单个的、不可再分的值，包括字符串、布尔值、整数、浮点数、Null、时间、日期。

测试配置文件定义了一个key为space，value也是一个map类型的节点，该map有两个kv对，它们的key分别是vec、num，value分别是数组类型和纯量类型。如下

test_config.yml:

space:vec: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]num: 7

测试代码：

void test_logConfig(){// 创建配置变量lunar::ConfigVar<std::vector<int>>::ptr vec = lunar::ConfigVarMgr::GetInstance()->lookUp("space.vec", std::vector<int>(), "vec test");lunar::ConfigVar<int>::ptr num = lunar::ConfigVarMgr::GetInstance()->lookUp("space.num", int(), "num test");// 解析配置文件lunar::ConfigVarMgr::GetInstance()->loadFromFile("test_config.yml");// 反序列化配置 && 输出到控制台LUNAR_LOG_INFO(g_logger) << vec->toString();LUNAR_LOG_INFO(g_logger) << num->toString();
}

解析结果：

[root@localhost build]# ../bin/test_config 
2024-01-31 21:02:02     2433    unknow  4294967295      [INFO]  [system]        /root/workspace/lunar/tests/test_config.cc:53       - 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
2024-01-31 21:02:02     2433    unknow  4294967295      [INFO]  [system]        /root/workspace/lunar/tests/test_config.cc:54       7

配置模块类的设计

在Yaml提供的数据类型的基础上，我们的配置文件还需要支持对象类型，所以我们需要通过模板，以泛型编程的方式实现对复杂数据类型的解析，除此之外，我们还要，对各个配置变量进行集中管理，综上所述，类的设计如下：

  1. LexicalCast，对象转换类模板（仿函数），使用C++的模板二次封装Boost库的boost::lexical_cast模板函数，实现基础类型和字符串类型间相互转换。然后对LexicalCast类模板进行偏特化，让其支持C++标准库的容器的序列化与反序列化。所以，我们实现的LexicalCast类模板默认支持基础类型和C++容器，想要支持自定义类型的序列化和反序列化，用户需要自己实现全特化LexicalCast。

  2. ConfigVarBase，配置变量基类，抽象出配置参数共有属性和方法比如变量名、对变量的描述、互斥锁、toString()、fromString()等，方便ConfigVarManager类使用多态对配置变量进行统一的管理。

  3. ConfigVar，配置变量类模板，继承ConfigVarBase类，含有m_value成员变量，利用LexicalCast类模板，实现toString方法将配置变量序列化成Yaml String，实现fromString方法将Yaml String反序列化成配置变量。此外，还支持变更通知，在set方法中调用变更回调，通知引用配置变量的地方更新变量。

  4. ConfigVarManager，配置变量管理类，利用std::map容器管理所有ConfigVar变量，std::map以配置变量名作为key，以配置变量基类智能指针作为value，支持配置变量的查询，用户在查询一条配置变量时，会提供该变量的变量名、默认值、变量描述，如果配置变量不存在，ConfigVarManager还会自动通过new 运算符利用默认值创建一个类型相同的配置变量，然后将<变量名，自动创建的配置变量>插到std::map中并返回给用户，因此ConfigVarManage还有自学习的能力。此外，提供了loadFromYaml函数支持对Yaml文件的解析，通过递归的方式解析Yaml文件中的每个map node节点，因为Yaml文件的map类型就是<key, value>对，这里key，value在配置文件中的含义和成员变量std::map中元素的含义是一致的,所以，取解析到的每个map node节点的key，去查该key是否存在于std::map成员中，如果存在，就调用相应配置变量基类的fronString函数，将map node的value作为参数，反序列化成一个配置变量。

ConfigVarManager的伪代码如下：

伪代码

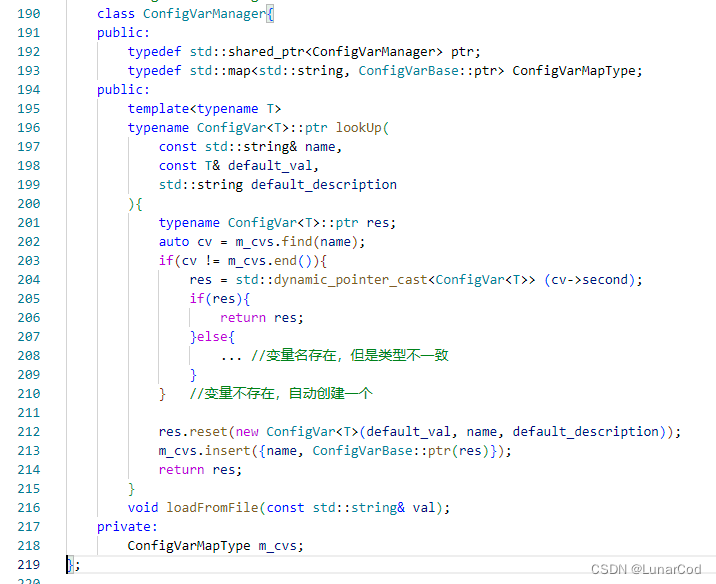
yaml配置文件解析的核心代码如下：

    // 递归枚举每一个类型为map的节点。static void __ListAllYamlNode(std::string prefix,const YAML::Node& node,std::vector<std::pair<std::string, YAML::Node>>& output){output.push_back(std::make_pair(prefix, node));if(node.IsMap()){for(auto it = node.begin(); it != node.end(); it++){__ListAllYamlNode((prefix.empty() ? prefix :prefix + ".") + it->first.Scalar(), it->second, output);}}}void ConfigVarManager::loadFromFile(const std::string& val){std::vector<std::pair<std::string, YAML::Node>> nodes;YAML::Node root = YAML::LoadFile(val);__ListAllYamlNode("", root, nodes);for(auto it = nodes.begin(); it != nodes.end(); it++){ConfigVarBase::ptr var = lookUpConfigVarBaseByName(it->first);if(var != nullptr){ // 有配置变量就解析该节点std::stringstream ss("");ss << it->second;var->fromString(ss.str());// for debug//LUNAR_LOG_DEBUG(LUNAR_LOG_NAME("system")) << var->toString();}}}

关于yaml-cpp的使用可以参考官方文档：https://github.com/jbeder/yaml-cpp/wiki/Tutorial。

感兴趣的同学，可以阅读一下本文实现的源码：https://github.com/LunarStore/lunar

本章完结

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/449808.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【24美赛思路已出】2024年美赛A~F题解题思路已出 | 无偿自提

【24美赛思路已出】2024年美赛A~F题解题思路已出 | 无偿自提

A题&#xff1a;资源可用性和性别比例 问题一&#xff1a; 涉及当灯鱼种群的性别比例发生变化时&#xff0c;对更大的生态系统产生的影响。为了分析这个问题&#xff0c;可以采用以下的数学建模思路&#xff1a;建立灯鱼种群模型&#xff1a; 首先&#xff0c;建立一个灯鱼种群…
阅读更多...
python爬虫4

python爬虫4

#1.练习 # &#xff08;1&#xff09; 获取网页的源码 # &#xff08;2&#xff09; 解析 解析的服务器响应的文件 etree.HTML # (3) 打印 import urllib.request urlhttps://www.baidu.com/ headers {User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit…
阅读更多...
CAD-autolisp（四）——编译

CAD-autolisp（四）——编译

目录 一、编译1.1 界面操作1.2 生成的应用程序&#xff08;二选一&#xff09; 二、后续学习 一、编译 编译&#xff1a;lsp后缀名为原文件&#xff0c;后缀名为fas、vlx为编译后文件&#xff0c;其会把sld、dcl、lsp等文件都编译进一个应用程序文件中加载&#xff1a;cad命令…
阅读更多...
【已更新】2024美赛C题代码教学思路数据处理数学建模分析Momentum in Tennis

【已更新】2024美赛C题代码教学思路数据处理数学建模分析Momentum in Tennis

问题一完整的代码已给出&#xff0c;预计2号晚上或者3号凌晨全部给出。 代码逻辑如下&#xff1a; C题第一问要求我们开发一个模型&#xff0c;捕捉得分时的比赛流程&#xff0c;并将其应用于一场或多场比赛。你的模型应该确定哪名球员在比赛的特定时间表现得更好&#xff0c;…
阅读更多...
DoubleEnsemble：基于样本重加权和特征选择的金融数据分析方法

DoubleEnsemble：基于样本重加权和特征选择的金融数据分析方法

现代机器学习模型&#xff08;如深度神经网络和梯度提升决策树&#xff09;由于其提取复杂非线性模式的优越能力&#xff0c;在金融市场预测中越来越受欢迎。然而&#xff0c;由于金融数据集的信噪比非常低&#xff0c;并且是非平稳的&#xff0c;复杂的模型往往很容易过拟合。…
阅读更多...
Zoho Projects与Jira：中国市场的理想替代品之争？

Zoho Projects与Jira：中国市场的理想替代品之争？

在软件开发生命周期中&#xff0c;项目管理一直是一个非常重要的环节。为了更好地协作、追踪项目的进程和管理任务&#xff0c;许多公司选择了Jira这款著名的项目管理工具&#xff0c;它是个非常强大的工具&#xff0c;但是作为一款纯国外产品&#xff0c;他可能不适合中国市场…
阅读更多...
【Nginx】nginx入门

【Nginx】nginx入门

文章目录 一、Web服务器二、Nginx三、Nginx的作用Web服务器正向代理反向代理 四、CentOS上安装Nginx(以CentOS 7.9为例) 一、Web服务器 Web 服务器&#xff0c;一般是指“网站服务器”&#xff0c;是指驻留于互联网上某种类型计算机的程序。Web 服务器可以向 Web 浏览器等客户…
阅读更多...
Http请求Cookie失效问题

Http请求Cookie失效问题

Http请求Cookie失效问题记录 一、问题现象 在开发功能的过程中&#xff0c;业务依赖cookie进行取之&#xff0c;项目进行交互时会对前端http请求携带的cookies进行解析操作&#xff0c;但在自测调试对过程中出现账户的授权失效的报错问题。 二、问题排查 用arthas进行代码方…
阅读更多...
【数据结构】双向链表 超详细 （含：何时用一级指针或二级指针；指针域的指针是否要释放）

【数据结构】双向链表 超详细 （含：何时用一级指针或二级指针；指针域的指针是否要释放）

目录 一、简介 二. 双链表的实现 1.准备工作及其注意事项 1.1 先创建三个文件 1.2 注意事项&#xff1a;帮助高效记忆 1.3 关于什么时候 用 一级指针接收&#xff0c;什么时候用 二级指针接收&#xff1f; 1.4 释放节点时&#xff0c;要将节点地址 置为NULL&#xff0…
阅读更多...
WPS Office18.7软件日常更新

WPS Office18.7软件日常更新

【应用名称】&#xff1a;WPS Office 【适用平台】&#xff1a;#Android 【软件标签】&#xff1a;#WPS 【应用版本】&#xff1a;18.6.1➡18.7 【应用大小】&#xff1a;160MB 【软件说明】&#xff1a;软件日常更新。WPS Office是使用人数最多的移动办公软件。独有手机阅读模…
阅读更多...
Blender教程（基础）-面的法向-12

Blender教程（基础）-面的法向-12

一、准备 新建如下图所示立方体演示面的法向 默认法向方向 二、显示法向 再菜单栏右上角、找到网络编辑模式&#xff0c;最下面的显示发法线打勾&#xff0c;如下图所示&#xff0c;出现的浅蓝色线条就是代表法向方向。 调整大小显示 三、正面 再显示叠加层菜单下找到面…
阅读更多...
day38 斐波那契数 爬楼梯 使用最小花费爬楼梯

day38 斐波那契数 爬楼梯 使用最小花费爬楼梯

题目1&#xff1a;509 斐波那契数 题目链接&#xff1a;509 斐波那契数 题意 斐波那契数列由0和1开始 后面的每一项数字都是前面两项数字之和 计算F(n) 动态规划 动规五部曲&#xff1a; 1&#xff09;dp数组及下标i的含义 dp[i] : 第i个斐波那契数值 i: 第i个斐…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023