算法介绍

核化线性降维是一种使用核方法（Kernel Methods）来进行降维的技术。在传统的线性降维方法中，例如主成分分析（PCA）和线性判别分析（LDA），数据被映射到一个低维线性子空间中。而核化线性降维则通过使用核技巧，将数据映射到一个非线性的低维空间中。

核技巧的核心思想是通过一个非线性映射将原始数据转换到一个高维的特征空间，然后在该特征空间中应用线性降维方法。这种映射可以使用核函数来实现，例如径向基函数核（RBF核）或多项式核。

下面我们以核主成分分析（KPCA）为例子：

假定我们将高维特征空间中把数据投影到由$\mathbf{W}$确定的超平面上，即PCA欲求解：

$$\left(\sum _{i=1}^m{z}_i{z}_i^T\right)\mathbf{W}=\lambda \mathbf{W}\text{\hspace{1em}(1)}$$

其中$z_i$是样本点$x_i$在高维特征空间中的像，可知：

$$\begin{array}{rl}\mathbf{W}& =\frac{1}{\lambda }\left(\sum _{i=1}^m{z}_i{z}_i^T\right)\mathbf{W}=\sum _{i=1}^m{z}_i\frac{z_i^T\mathbf{W}}{\lambda }\\ & =\sum _{i=1}^m{z}_i{\alpha }_i\end{array}\text{\hspace{1em}(2)}$$

其中${\alpha }_i=\frac{1}{\lambda }{z}_i^T\mathbf{W}$(权重)。假设$z_i$是通过原始空间中的样本点$x_i$通过映射$\varphi$产生，即$z_i=\varphi (x_i),i=1,2,...,m$。若能被$\varphi$显式的表达出来，通过它将样本映射到高维特征空间，再从高维特征空间中使用PCA，可将式（1）变化为：

$$(\sum _{i=1}^m\varphi (x_i)\varphi (x_i{)}^T)\mathbf{W}=\lambda \mathbf{W}\text{\hspace{1em}(3)}$$

式（2）变化为：

$$\mathbf{W}=\sum _{i=1}^m\varphi (x_i){\alpha }_i\text{\hspace{1em}(4)}$$

一般情况下我们不知道$\varphi$的 形式，故引入核函数：

$$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)\text{\hspace{1em}(5)}$$

将式（4）和式（5）带入式（3）中有：

已知$z_i=\varphi (x_i)$，类比 X = { x 1 , x 2 , . . . , x m } \mathbf{X}=\{x_1,x_2,...,x_m\} X={x1​,x2​,...,xm​}，可以构造出 Z = { z 1 , z 2 , . . . , z m } \mathbf{Z}=\{z_1,z_2,...,z_m\} Z={z1​,z2​,...,zm​}。
$$\begin{array}{rl}(\sum _{i=1}^m\varphi (x_i)\varphi (x_i{)}^T)w_j& ={\lambda }_j{w}_j\\ \left(\sum _{i=1}^m{z}_i{z}_i^T\right)w_j& ={\lambda }_j{w}_j\\ \mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}{w}_j& ={\lambda }_j{w}_j\\ \mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}\sum _{i=1}^m\varphi (x_i){\alpha }_i^j& ={\lambda }_j\sum _{i=1}^m\varphi (x_i){\alpha }_i^j\\ \mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}\sum _{i=1}^m{z}_i{\alpha }_i^j& ={\lambda }_j\sum _{i=1}^m{z}_i{\alpha }_i^j\\ \mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}\mathbf{Z}{\alpha }^j& ={\lambda }_j\mathbf{Z}{\alpha }^j\\ \mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}\mathbf{Z}{\alpha }^j& =\mathbf{Z}{\lambda }_j{\alpha }^j\\ {\mathbf{Z}}^{\mathbf{T}}\mathbf{Z}{\alpha }^j& ={\lambda }_j{\alpha }^j\end{array}\text{\hspace{1em}(6)}$$
其中${\mathbf{\alpha }}^j=\left({\alpha }_1^j;{\alpha }_2^j;\dots ;{\alpha }_m^j\right)\in {\mathbb{R}}^{m\times 1}$

令$\mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}=\mathbf{K}$，那么上式可化为：

$$\mathbf{K}{\alpha }^j={\lambda }_j{\alpha }^j\text{\hspace{1em}(7)}$$

其中矩阵$\mathbf{K}$的第$i$行第$j$列的元素${\mathbf{K}}_{ij}=z_i^T{z}_j=\varphi (x_i{)}^T\varphi (x_j)=\kappa (x_i,x_j)$。

显然式（7）是一个特征值分解问题，取$\mathbf{K}$最大的$d^{\prime }$个特征值所对应的特征向量即可。

对新样本$x=(x_1,x_2,...,x_m)$（向量），其向高维特征空间的投影后的第$j(j=1,2,...,d^{\prime })$维坐标是：

$$\begin{array}{rl}{z}^j& =w_j^T\varphi (x)\\ & =\sum _{i=1}^m{\alpha }_i^j\varphi (x_i{)}^T\varphi (x)\\ & =\sum _{i=1}^m{\alpha }_i^j\kappa (x_i,x)\end{array}\text{\hspace{1em}(8)}$$

算法过程与PCA算法类似。

实验分析

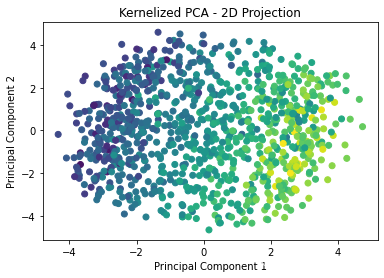
数据集如下图所示：

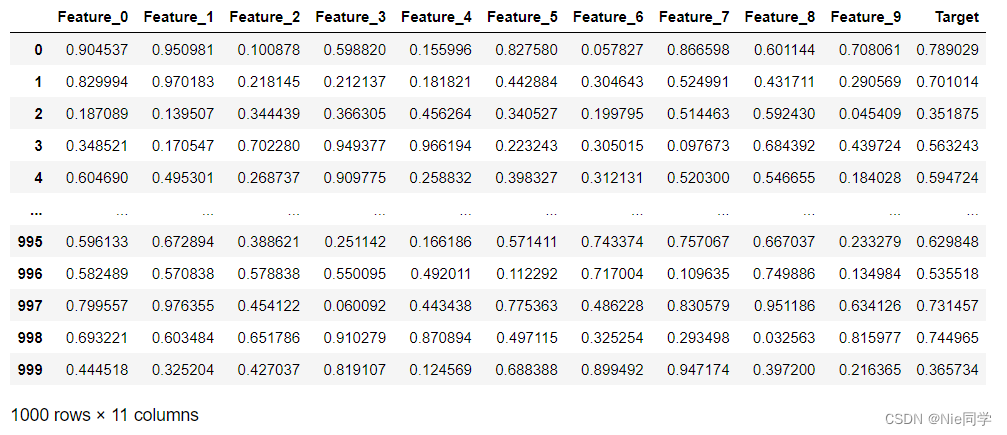
读入数据集：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 读取数据集
data = pd.read_csv('data/correlated_dataset.csv')# 提取特征和目标
X = data.drop('Target', axis=1).values
y = data['Target'].values

定义核函数：

# 核函数（径向基函数）
def rbf_kernel(x, y, gamma=1.0):return np.exp(-gamma * np.linalg.norm(x - y)**2)

计算以及中心化核矩阵：

# 计算核矩阵
def compute_kernel_matrix(X, gamma=1.0):n_samples = X.shape[0]K = np.zeros((n_samples, n_samples))for i in range(n_samples):for j in range(n_samples):K[i, j] = rbf_kernel(X[i], X[j], gamma)return K# 中心化核矩阵
def center_kernel_matrix(K):n_samples = K.shape[0]one_n = np.ones((n_samples, n_samples)) / n_samplesK_centered = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)return K_centered

计算特征值与特征向量：

# 计算特征值和特征向量
def compute_eigenvectors(K_centered, n_components):eigvals, eigvecs = np.linalg.eigh(K_centered)# 选择前n_components个最大特征值对应的特征向量idx = np.argsort(eigvals)[::-1][:n_components]return eigvecs[:, idx]

执行KPCA并绘制降维可视化结果：

# 数据中心化
X_centered = X - np.mean(X, axis=0)# 计算核矩阵
K = compute_kernel_matrix(X_centered)# 中心化核矩阵
K_centered = center_kernel_matrix(K)# 选择降维后的维度
n_components = 6# 计算特征向量
eigenvectors = compute_eigenvectors(K_centered, n_components)# 降维
X_pca = K_centered.dot(eigenvectors)# 可视化降维结果
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.title('Kernelized PCA - 2D Projection')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()