🔥博客主页： A_SHOWY
🎥系列专栏：力扣刷题总结录 数据结构 云计算 数字图像处理 力扣每日一题_
【1】三角形类型Ⅱ
100222. 三角形类型 II
https://leetcode.cn/problems/type-of-triangle-ii/
简单题，直接过了
class Solution {
public:string triangleType(vector<int>& nums) {if(nums[0] + nums[1] <= nums[2] ||nums[0] + nums[2] <= nums[1] || nums[2] + nums[1] <= nums[0]) return "none";else{if(nums[0] == nums[1] && nums[0] == nums[2]) {return "equilateral";}else if(nums[0] == nums[1] ||nums[2] == nums[1] ||nums[0] == nums[2]) {return "isosceles";}else {return "scalene";}}}
};【2】人员站位的方案数
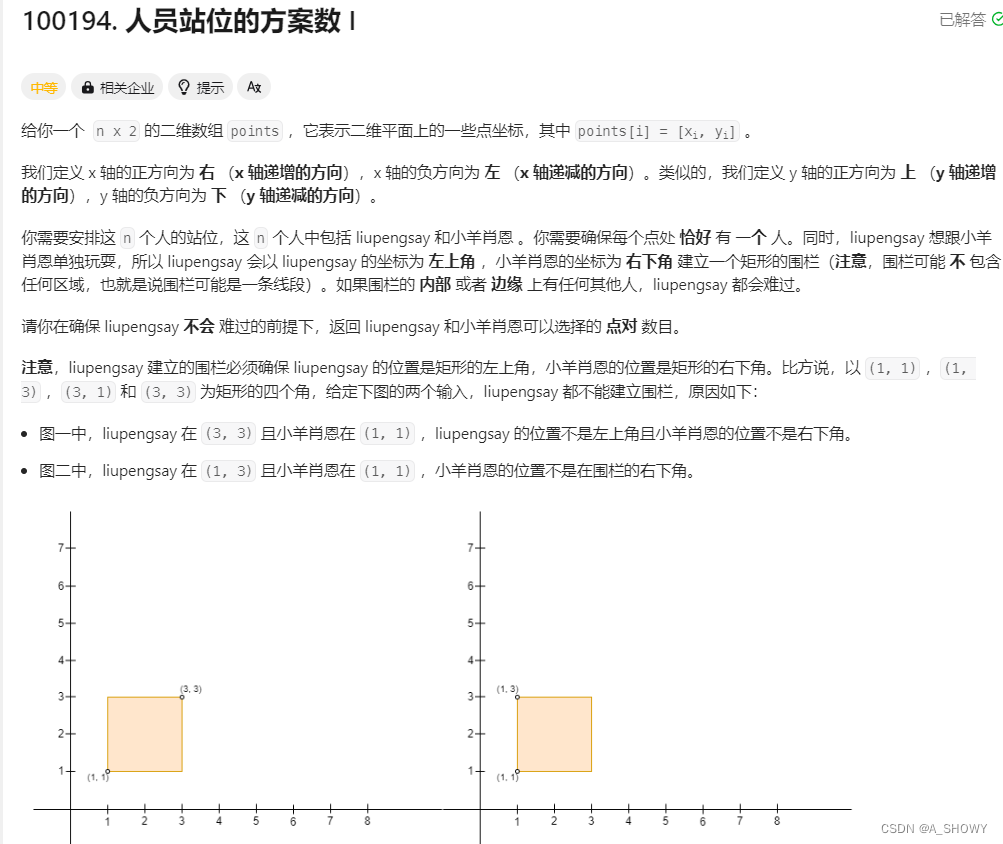
100194. 人员站位的方案数 Ihttps://leetcode.cn/problems/find-the-number-of-ways-to-place-people-i/
是一个二维数组的题目，用到一个小技巧，判断这个矩形里面有没有数，可以按照行坐标排序从小到大，再对相同行坐标的从大到小排序，降低维度了。然后进行枚举
判断范围内有没有点，技巧是先把这个points排序，比如按照横坐标从小到大，那么后续的枚举只需要考虑纵坐标即可。如果横坐标相同，从上到下枚举。
这样我们只需要考虑下一个点的纵坐标是否比我们当前定义的最大值要大，保证大才能满足不包含点。
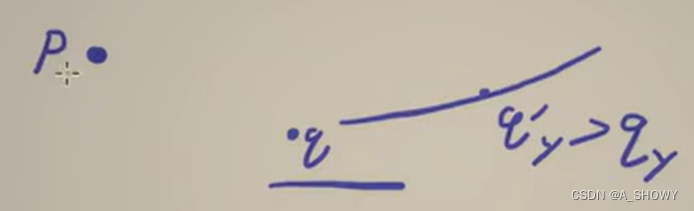
class Solution {
public:int numberOfPairs(vector<vector<int>>& points) {ranges::sort(points,[](const auto &p,const auto &q){return p[0] != q[0] ? p[0] < q[0] : p[1] > q[1];});int ans = 0;int n = points.size();for(int i = 0; i < n ; i++){// 记录第一个的yint y0 = points[i][1];// 记录比第一个的y小的，初始值设置为最小int max_y = INT_MIN;for(int j = i + 1; j < n; j++){int y = points[j][1];if(y <= y0 && y > max_y) {max_y = y;ans++;}}}return ans;}
};【3】最大子数组和
100183. 最大好子数组和https://leetcode.cn/problems/maximum-good-subarray-sum/
这个题目太可惜了，其实如果暴力思路不算难的，比赛的时候我先是，用了一个o（n的三次方的方法超时），然后优化了一下前缀和o（n方）还是超时！我人就麻了，最后几个用例一直通不过，今天看了题解动态的维护前缀和，太巧妙了
方法一：前缀和+模拟双重循环
class Solution {
public:long long maximumSubarraySum(vector<int>& nums, int k) {int n = nums.size();long long ans = INT_MIN;vector<long long> preSum(n + 1, 0);for (int i = 0; i < n; ++i) {preSum[i + 1] = preSum[i] + nums[i];}for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {int diff = abs(nums[i] - nums[j]);if (diff == k) {ans = max(ans, preSum[j + 1] - preSum[i]);}}}if(ans != INT_MIN)return ans;else return 0;}
};（超时，4个长用例过不去）
方法二：动态维护前缀和
- 为了方便描述把nums数组描述为a。子数组a[i 。。。j]的元素和为s[j + 1] - s[ i ]（因为s这个数组首项为0。我们的总体思路是枚举j，找到最小的s[ i ]满足| a[ i ] - a[ j ] | = k。定义哈希表sum_s，键为a[i] 值为相同a[i] 下的s[i] 的最小值。
- 核心就是遍历右边，左边找合适的存到哈希表，并且动态维护这个值的最小前缀和。
class Solution {
public:long long maximumSubarraySum(vector<int>& nums, int k) {long long ans = LLONG_MIN;long long sum = 0;unordered_map<int , long long> min_s;for(int x : nums){auto it = min_s.find(x - k);if(it != min_s.end()){ans = max(ans,sum + x - it->second);}it = min_s.find(x + k);if(it != min_s.end()){ans = max(ans,sum + x - it -> second);}// 找最小的那个满足条件的左边的值，遍历所有的当右边的值it = min_s.find(x);if(it == min_s.end() || sum < it -> second){min_s[x] = sum;}sum += x;}return ans == LLONG_MIN ? 0 : ans;}
};
