场景
上一章学习了代价函数,在机器学习中,代价模型是用于衡量模型预测值与真实值之间的差异的函数。它是优化算法的核心,目标是通过调整模型的参数来最小化代价模型的值,从而使模型的预测结果更接近真实值。常见的代价模型是均方误差(Mean Squared Error,MSE),它衡量了模型预测值与真实值之间的平方差的平均值。上一章曾经简单得用它预测过房价,MSE可以表示为:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
其中, J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 是代价模型, h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i)) 是模型对第 i i i 个样本的预测值, y ( i ) y^{(i)} y(i) 是第 i i i 个样本的真实值, m m m 是训练样本数量。
梯度下降算法是一种优化算法,用于最小化代价模型。它通过迭代的方式,沿着代价函数的负梯度方向更新模型的参数,以逐步接近最优解。在每次迭代中,梯度下降算法计算代价函数对于每个参数的偏导数(即梯度),然后按照一定的学习率更新参数。
具体来说,在线性回归中,梯度下降算法的更新规则可以表示为:
θ 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \theta_0 := \theta_0 - \alpha \frac{\partial J(\theta_0, \theta_1)}{\partial \theta_0} θ0:=θ0−α∂θ0∂J(θ0,θ1)
θ 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \theta_1 := \theta_1 - \alpha \frac{\partial J(\theta_0, \theta_1)}{\partial \theta_1} θ1:=θ1−α∂θ1∂J(θ0,θ1)
其中, α \alpha α 是学习率,控制参数更新的步长。
想象
你可以想象你在黄山上,你要到达上山得最低点,每一次你都会根据你自己现在得位置选择向哪里行动,例如:你现在得位置在这里

现在往下走,你可以往下迈一小步,也可以迈一大步。

你往下走了,这无可非议,当你走到这里得时候,
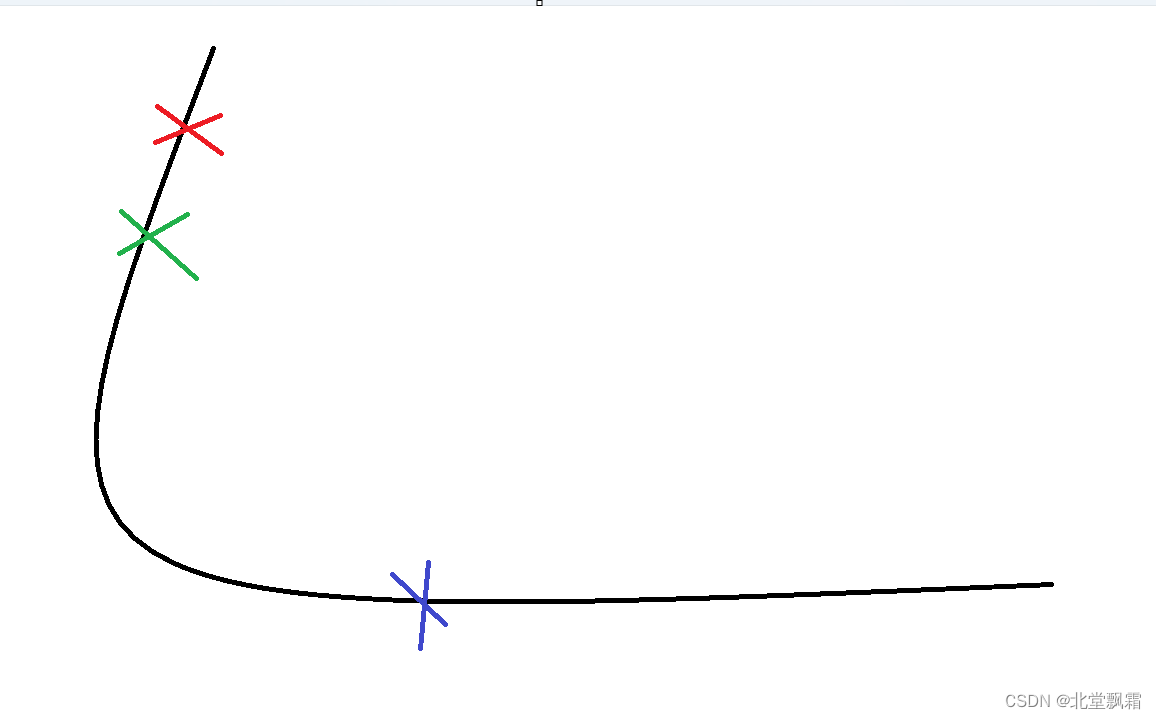
你认为已经在最下面了,已经找不到哪里才是更下了,这时候变不再走了。
这个过程可以描述为:假设你在一个山谷中寻找最低点,你的目标是找到山谷的最低处。
首先,你选择一个起始点,可以是山谷的任意位置。然后,你观察当前位置的海拔高度,这可以看作是目标函数的值。
接下来,你想找到一个下山的方向,即找到一个使海拔高度下降最快的方向。这个方向可以通过计算当前位置的梯度来确定。梯度是一个向量,指示了在当前位置函数值增长最快的方向。
你会朝着梯度的反方向移动一小步,这样你就能够下山。这个步长可以通过学习率来控制,学习率决定了你每次迈出的步子有多大。
然后,你到达了新的位置,你再次观察海拔高度,并计算新位置的梯度。你会继续朝着梯度的反方向移动,不断重复这个过程,直到达到停止条件。
停止条件可以是达到最大迭代次数、函数值变化小于某个阈值或者梯度的范数(长度)小于某个阈值等。这样,你就能够找到山谷的最低点,也就是目标函数的最小值点。
总结起来,梯度下降算法可以被看作是在山谷中寻找最低点的过程。通过计算函数的梯度,朝着梯度的反方向移动一小步,不断重复这个过程,直到达到停止条件,从而找到目标函数的最小值点。
结束
这都是一些梯度下降算法的概念,其实结合起来比较简单了,首先上一章的代价函数是找一个最接近y的值,这一章梯度算法实际上就是,当然,你可以理解为,我初始化我的两个变量 Y = A + BX
A,B为(0,0),随后你选择步长为0.01,迭代一千次,带入公式反复计算
for j in range(parameters):term = np.multiply(error, X[:,j])temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term)) theta = temp---代价函数 TODO---return theta, cost
θ 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \theta_0 := \theta_0 - \alpha \frac{\partial J(\theta_0, \theta_1)}{\partial \theta_0} θ0:=θ0−α∂θ0∂J(θ0,θ1)
θ 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \theta_1 := \theta_1 - \alpha \frac{\partial J(\theta_0, \theta_1)}{\partial \theta_1} θ1:=θ1−α∂θ1∂J(θ0,θ1)
类比:每一个下山的脚步就是步长alpha ,alpha 越大,下降越快,暂时可以这么理解。