何为剪枝,就是减少搜索树的大小。
它有什么作用呢?
1.改变搜索顺序。
2.最优化剪枝。
3.可行性剪枝。

首先,单纯的广搜是无法实现的,因为它存在来回跳的情况来拖时间。
于是我们可以用DFS,那我们如何剪枝呢?
1.已经超时了还没到------舍弃
2.沿最快的路径(忽视障碍物)仍无法在规定时间到----舍弃
3.我们用x,y计算出两者的距离(不考虑障碍物),我们考虑反悔的时间,它是反悔后到的地方时间+偶数(有来必有回),就算有障碍物,要到目标肯定是两者的距离+返回时间,于是我们可以用这奇偶性与T判断,不同就删。
4.在此,我们可以确定,我们可以先BFS求最小+奇偶性判断即可。
让我们看另外一道:

下面是分析:
1.我们可以先sort,从小到大排,遇到正确的就退出。
2.参考组合的题,我们可以固定同一个木棒上的组成从大到小。
3.我们应该先放大的,并且从左开始(因为从小开始的话枚举了很多多会被最长的判断掉,比较严谨的可以看看上次写的数独问题)
4.结尾木棒如果错,则不是它的问题(我们要替代只能用跟小的组合,显然不划算)
5.开头木棒如果错,则是上一根木棒的问题(因为这木棒迟早要用,如果它错了,其他的木棒也不会对)
6.一个木棒不行,那么和他长度一样的也不可以。
因此,我们可以用上述规则剪枝。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[100],sum;
int b[100];
bool cmp(int a,int b){return a>b;
}//nxt剩下的棍子,len;changdu;chan:shenxia changdu
int q[1000][100];
int dfs(int nxt,int len,int chan,int pos){if(nxt==0&&chan==0) return 1;if(chan==0){chan=len;nxt--;pos=0;}for(int i=pos+1;i<=n;i++){if(b[i]!=0) continue;if(a[i]>chan) continue;if(q[chan][i]==-1) continue;b[i]=1;if(dfs(nxt,len,chan-a[i],i)==1) return 1;q[chan][i]==-1;b[i]=0;if(chan==len||chan==a[i]) return 0;while(a[i+1]==a[i]) i++;}return 0;
}
int main(){cin>>n;int y;for(int i=1;i<=n;i++){scanf("%d",&a[i]);sum+=a[i];}sort(a+1,a+n+1,cmp);for(int i=1;i<=3000;i++){if(sum%i!=0) continue;y=i;int u=sum/i;if(dfs(u-1,i,i,0)==1) break;}cout<<y;
}再来一道:
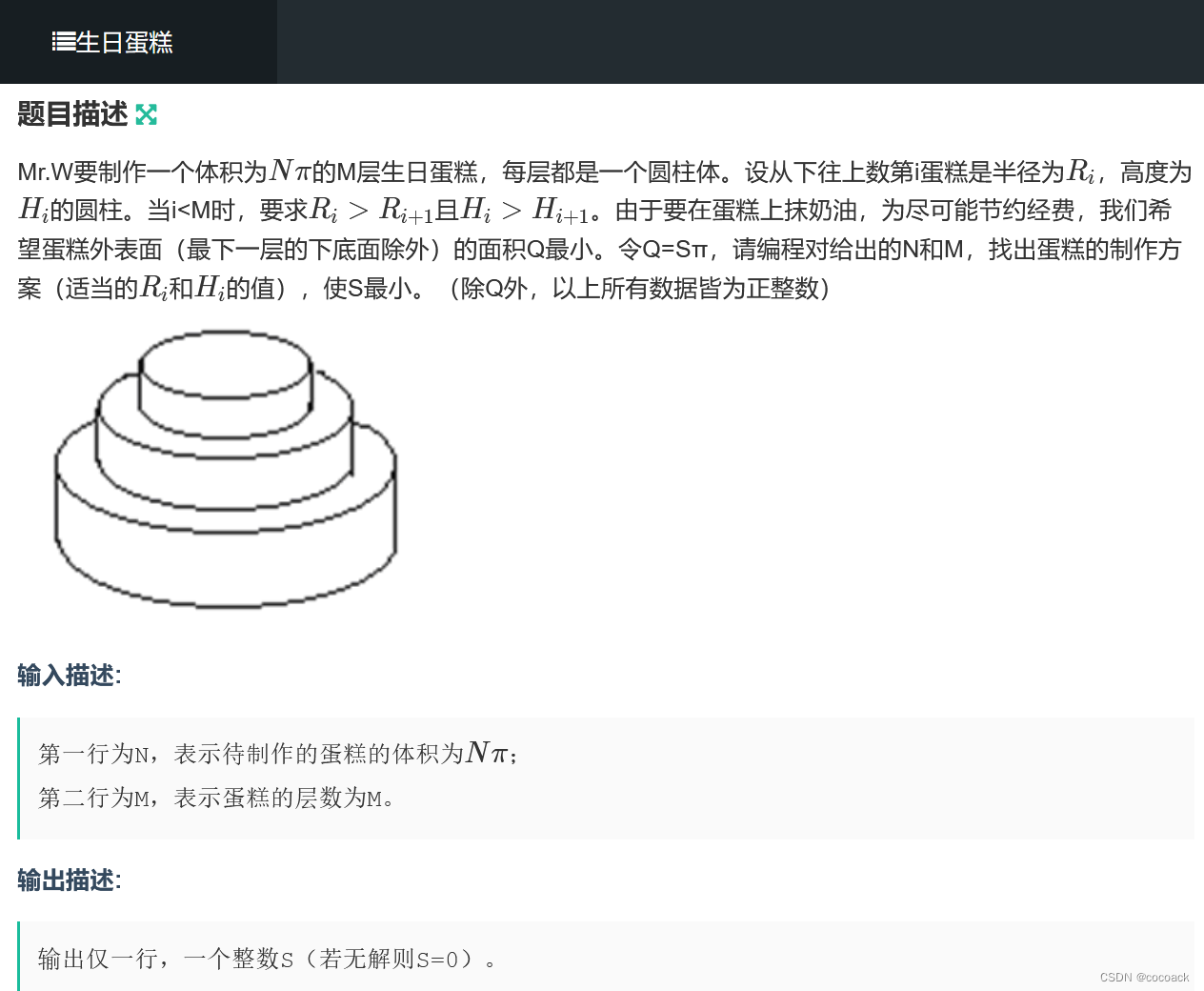
下面是分析:

下面再对几个剪枝分析一下:
从m层dep层:
对于每一层的R 另h=1---->
同理:
注意:枚举r,h时要从大到小
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,_s[23],_v[23],min1=1000000;
void dfs(int r,int h,int c,int v,int s){if(c==m){if(v==n) min1=min(min1,s);return ;}if(v+_v[c]>n) return;if(s+_s[c]>min1) return;if(2*(n-v)/r+s>min1) return;for(int i=min(r-1,(int)sqrt(n-v));i>=m-c;i--){if(c==0) s=i*i;for(int j=min(h-1,(n-v)/(i*i));j>=m-c;j--){dfs(i,j,c+1,v+i*i*j,s+2*i*j);}}
}
int main(){cin>>n>>m;for(int i=m;i>=0;i--) _s[i]=_s[i+1]+2*(m-i)*(m-i);for(int i=m;i>=0;i--) _v[i]=_v[i+1]+(m-i)*(m-i)*(m-i);dfs(n,n,0,0,0);if(min1==1000000) cout<<0;else cout<<min1;
}