🙊前言：本文章为瑞_系列专栏之《数据结构与算法》的B树篇。由于博主是从B站黑马程序员的《数据结构与算法》学习到的相关知识，所以本系列专栏主要针对该课程进行笔记总结和拓展，文中的部分原理及图解也是来源于黑马提供的资料。本文仅供大家交流、学习及研究使用，禁止用于商业用途，违者必究！

相关知识链接：二叉树
相关知识链接：二叉搜索树
相关知识链接：AVL树
相关知识链接：红黑树

1 什么是B树

1.1 B树的背景

  B树（B-Tree）结构是一种高效存储和查询数据的方法，它的历史可以追溯到1970年代早期。B树的发明人Rudolf Bayer和Edward M. McCreight分别发表了一篇论文介绍了B树。这篇论文是1972年发表于《ACM Transactions on Database Systems》中的，题目为"Organization and Maintenance of Large Ordered Indexes"。

  这篇论文提出了一种能够高效地维护大型有序索引的方法，这种方法的主要思想是将每个节点扩展成多个子节点，以减少查找所需的次数。B树结构非常适合应用于磁盘等大型存储器的高效操作，被广泛应用于关系数据库和文件系统中。

  B树结构有很多变种和升级版，例如B+树，B*树和SB树等。这些变种和升级版本都基于B树的核心思想，通过调整B树的参数和结构，提高了B树在不同场景下的性能表现。

  总的来说，B树结构是一个非常重要的数据结构，为高效存储和查询大量数据提供了可靠的方法。它的历史可以追溯到上个世纪70年代，而且在今天仍然被广泛应用于各种场景。

  瑞：本系列介绍过的自平衡的树如AVL树、红黑树的增删改查效率在内存中能达到对数级别，属于高效率的，但是并不适合做磁盘（IO）上的增删改查，而B树就比较适合，如MySQL底层是使用的B树结构升级版B+树。

  对树进行增删改查操作的效率主要取决于树的高度，树的高度越低，比较次数越少，反之亦然。如果是100W的数据，用AVL树存储，树的高度会达到20，因为log2(1000000)约等于20。最糟糕的情况下，要比较到叶子节点即20次才能找到数据，那在磁盘上要做20次读写，这是非常耗时的操作，导致效率低下。但是同样的100W数据，存储在B-树中（最小度数是500），树的高度约为3，平均效率有显著提升，所以在对于磁盘上的增删改查操作，B树更为受到欢迎。

  所以B树大个特点就是：树的高度能降到非常的低，具体见下文分析

1.2 B 的含义

  B-树的名称是由其发明者Rudolf Bayer提出的。Bayer和McCreight从未解释B代表什么，人们提出了许多可能的解释，比如Boeing、balanced、between、broad、bushy和Bayer等。但McCreight表示，越是思考B-trees中的B代表什么，就越能更好地理解B-trees

瑞：本文中出现的B-树和B树是同一个概念的不同称呼，并没有实质性的区别。通常，当我们提到B树时，可能会看到它被写作B-tree、B tree或者B_tree，这些都是指同一种数据结构。B树的变种如B+树和B*树，这些才是不同的概念。BTree又叫多路平衡搜索树。

1.3 B-树的度和阶

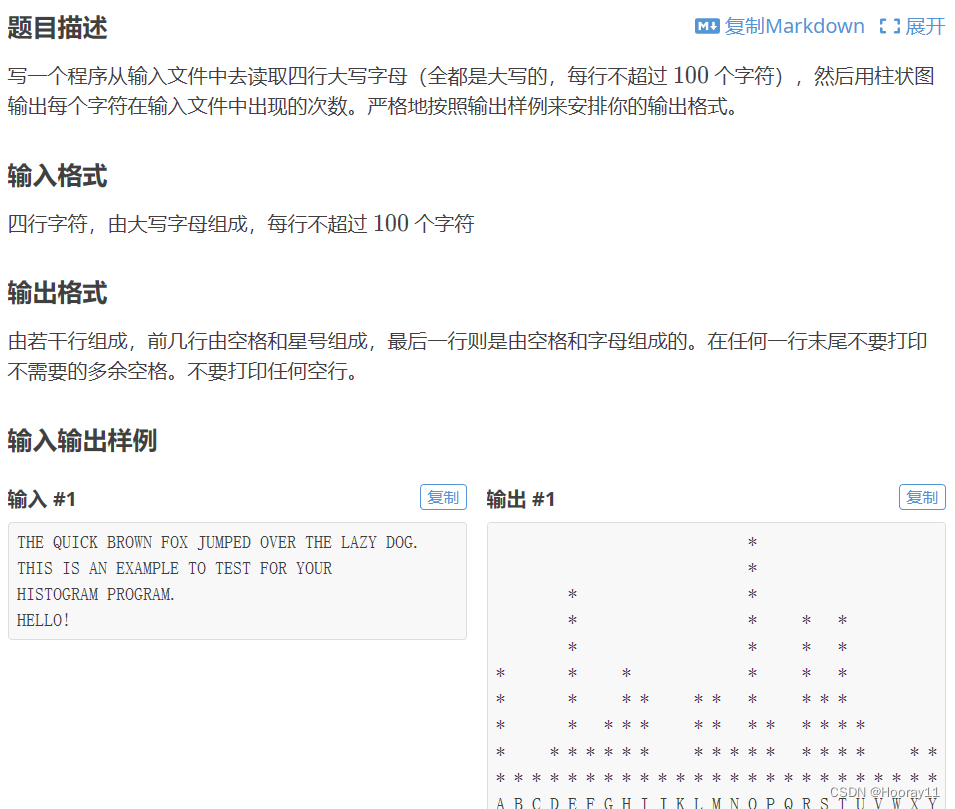
• 度（degree）：指树中节点孩子数
• 阶（order）：指所有节点孩子数最大值

  如上图：度：节点4、2都是有两个孩子，所以度数为2；节点1、3、5、7、9 10都是没有孩子，所以度数为0；节点6 8有3个孩子，所以度数为3。而阶是指上图中树的所有节点中孩子最多的那个值，就是节点6 8有3个孩子，所以上图中树的阶数为3。

1.4 B-树的特性

一颗m叉的BTree特性如下 ：

1. 树中每个节点最多包含 m 个孩子，其中 m 称为B-树的阶。
2. 除根节点与叶子节点外，其它每个节点至少有 ceil(m/2) 个孩子。
3. 若根节点不是叶子节点，则至少有两个孩子。
4. 所有的叶子节点都在同一层。
5. 每个非叶子节点由 n 个关键字 key 与 n+1 个指针组成，其中 ceil(m/2)-1 <= n <= m-1 。
6. 关键字按非降序排列，即节点中的第 i 个关键字大于等于第 i-1 个关键字。
7. 指针 P[ i ] 指向关键字值位于第 i 个关键字和第 i+1 哥关键字之间的子树。

瑞：
  根据第2条，中间节点的孩子数目是有下限的（阶数除以2，向上取整）。
  第5点中的n+1个指针就是n+1个孩子即孩子数目比该节点key的数目多1，如节点2有两个孩子（节点1、节点3）、节点6 8有3个孩子（节点5、节点7、节点9 10）
  最小度数要大于等于2（小于2意味着孩子只有一个，违反了B树的规则）B树中有最小度数的限制是为了保证B树的平衡特性
  最小度数 * 2 = 可能拥有的最多孩子的个数

  在B树中，每个节点都可以有多个子节点，这使得B树可以存储大量的键值，但也带来了一些问题。如果节点的子节点数量太少，那么就可能导致B树的高度过高，从而降低了B树的效率。此外，如果节点的子节点数量太多，那么就可能导致节点的搜索、插入和删除操作变得复杂和低效。
  最小度数的限制通过限制节点的子节点数量，来平衡这些问题。在B树中，每个节点的子节点数量都必须在一定的范围内，即t到2t之间（其中t为最小度数）

一棵 B-树具有以下性质：

  特性1️⃣：每个节点 x 具有

    1️⃣➖1️⃣ 属性 n，表示节点 x 中 key 的个数
    1️⃣➖2️⃣ 属性 leaf，表示节点是否是叶子节点
    1️⃣➖3️⃣ 节点 key 可以有多个，以升序存储

---

  特性2️⃣：每个非叶子节点中的孩子数是 n + 1、叶子节点没有孩子

---

  特性3️⃣：最小度数t（节点的孩子数称为度）和节点中键数量的关系如下：

Column 1	Column 2
最小度数t	键数量范围
2	1 ~ 3
3	2 ~ 5
4	3 ~ 7
…	…
n	(n-1) ~ (2n-1)

  其中，当节点中键数量达到其最大值时，即 3、5、7 … 2n-1，需要分裂

---

  特性4️⃣：叶子节点的深度都相同

瑞：即所有的叶子节点都在同一层

  B-树与 2-3 树、2-3-4 树的关系

  它们之间的关系：

1. 2-3树是最小度数为2的B树，其中每个节点可以包含2个或3个子节点。
2. 2-3-4树是最小度数为2的B树的一种特殊情况，其中每个节点可以包含2个、3个或4个子节点。
3. B树是一种更加一般化的平衡树，可以适应不同的应用场景，其节点可以包含任意数量的键值，节点的度数取决于最小度数t的设定。

1.5 B-树演变过程示例

  以5叉BTree为例（度为5）为例，演示B树的演变过程

  key的数量：可以根据公式推导ceil(m/2)-1<=n<=m-1。因为m为5，所以得2<=n<=4，即当n>4时，中间节点分裂到父节点，两边节点分裂。

  BTree可视化网站，点击进入https://www.cs.usfca.edu/~galles/visualization/BTree.html

  瑞：该网站是一个旧金山大学计算机科学系的可视化项目网站，专门用于展示和解释B树（B-tree）数据结构及其操作的可视化模型。

  下面就通过使用该网站对插入CNGAHEKQMFWLTZDPRXYS数据进行演示

  演变过程如下：

  进入网页后，选择Max. Degree = 5选项。本例模拟的是度数为5的情况下插入CNGAHEKQMFWLTZDPRXYS数据，后续网址和下半部分的配置不会再进行截取（均不会更改）

  1️⃣ 依次插入前4个字母CNGA后，B树演变为下图，此时B树为 4 个关键字 key（ACGN） 与 n+1 = 5 个指针组成

  2️⃣ 插入H，此时 n>4，中间元素G字母向上分裂到新的节点，分裂动图如下所示（后续分裂均是同理，过程可以到网站内自己感受，后续不再放置动图）

  此时B树各个key和指针的关系如下图所示（每一个节点指针比key的数量多1，后续不再展示带指针图）

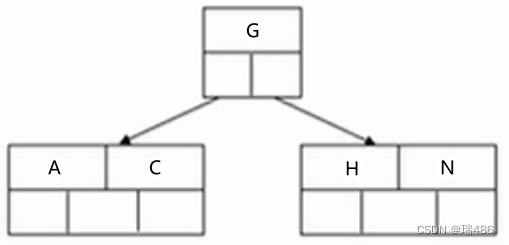
  3️⃣ 插入E、K、Q不需要分裂

  4️⃣ 插入M，中间元素M字母向上分裂到父节点G

  5️⃣ 插入F、W、L、T不需要分裂

  6️⃣ 插入Z，中间元素T向上分裂到父节点中

  7️⃣ 插入D，中间元素D向上分裂到父节点中，然后插入P、R、X、Y不需要分裂

  8️⃣ 最后插入S，NPQR节点n>5，中间节点Q向上分裂，但分裂后父节点DGMT的n>5，中间节点M向上分裂

  最终如下B树演化结果如下：

---

2 B-树的Java实现

1️⃣➖1️⃣ 内部节点类Node中含有属性：

• 关键字
• 孩子们
• 有效关键字个数
• 是否是叶子节点
• 最小度数 (最小孩子数)

瑞：由于本例关键字使用基本数组int[]存储，所以需要有效关键字个数属性对关键字个数进行记录，如果关键字使用集合（如List）则可以通过size方法获取到有效关键字个数

1️⃣➖2️⃣ 内部节点类Node中含有方法：

• 多路查找get(int key)
• 向指定索引处插入key(int key, int index)
• 向指定索引处插入child(Node child, int index)
• （后续更新）

2.1 B树节点类Node

  实际 keys 应当改为 entries 以便同时保存 key 和 value，本文主要是为了学习B树的思想，所以做简化实现

    static class Node {/*** 关键字*/int[] keys;/*** 孩子们*/Node[] children;/*** 有效关键字个数*/int keyNumber;/*** 是否是叶子节点*/boolean leaf = true;/*** 最小度数 (最小孩子数)，它决定了节点中key 的最小、最大数目，分别是 t-1 和 2t-1*/int t;/*** 构造方法（给最小度数赋值** @param t 最小度数（t>=2）*/public Node(int t) {this.t = t;this.children = new Node[2 * t];this.keys = new int[2 * t - 1];}public Node(int[] keys) {this.keys = keys;}/*** 打印有效Key，为了方便调试和测试，非必须*/@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}}

（后续内容明天更新）

---

本文是博主的粗浅理解，可能存在一些错误或不完善之处，如有遗漏或错误欢迎各位补充，谢谢

  如果觉得这篇文章对您有所帮助的话，请动动小手点波关注💗，你的点赞👍收藏⭐️转发🔗评论📝都是对博主最好的支持~