最近刷了一些关于基础数学问题的题目,大致是关于组合数、分解质因数还有一些思维题,题目来自洛谷的【数学1】基础数学问题 - 题单 - 洛谷,很多思路还是之前没有见过的,都是简单到一般难度的题目(橙、题、绿题),特别做个整理。
目录
组合数问题
编号
组合数问题
分解质因数
Hankson 的趣味题
细胞分裂
思维题
找筷子
进制转换
又是毕业季II
组合数问题
编号
编号 - 洛谷
这一题的意思就是有若干个位置,每个位置的数字范围都是 1~M[i],每个位置放置的数字都不相同,有多少排列数。
首先升序排序,因为选择更少的一定是先排,前面范围小的可以选择的,后面范围大的也一定可以选择,而且前面排列的也一定是后面拍的其中一个选择,那么对于位置x,此时的选择就有M[i]-x+1,总的排列数量就是(M[1]-1+1)*(M[2]-2+1)*...*(M[n]-n+1),显然若其中任意一个数为0,也就是到这个位置,没有选择了,那么就是无法满足。
记得随时取模。
#include<stdio.h>
#include<algorithm>
using namespace std;
#define ll long long
#define MOD 1000000007int cmp(int x, int y) {return x < y;
}int a[100];
int main()
{int n; scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", a+i);}sort(a + 1, a + n + 1, cmp); // 升序排序首先需要计算出所有的组合数ll ans = 1;for (int i = 1; i <= n; i++) {if (a[i] < i) {printf("0\n");return 0;}ans = ans * (a[i]-i+1) % MOD;}printf("%lld\n", ans);return 0;
}组合数问题
[NOIP2016 提高组] 组合数问题 - 洛谷
这一题略复杂,需要计算对于所有0<i≤n,0<j≤min(i,m),有多少对(i,j)满足k|C(i,j),其中X|Y定义为Y mod X = 0。
对于排列数C(n,m),存在C(n,m)=C(n-1,m-1)+C(n-1,m),也就是在n个东西里面选m个东西,等于除掉任意一个东西x,选x并且在剩下n-1个选m-1的情况,加上在n-1个里面选m个东西,(学过排列组合应该能get?),也可以从代数角度证明等式。这个在图形中就表现为杨辉三角,这也是这一题计算任意C(i,j)的关键所在。
预处理出杨辉三角后存在数组中,此时问题就变成了在一个杨辉三角中画一个矩形,计算矩形中有多少个满足的点,就比如下面计算样例1的i=3,j=3有多少满足2的倍数。
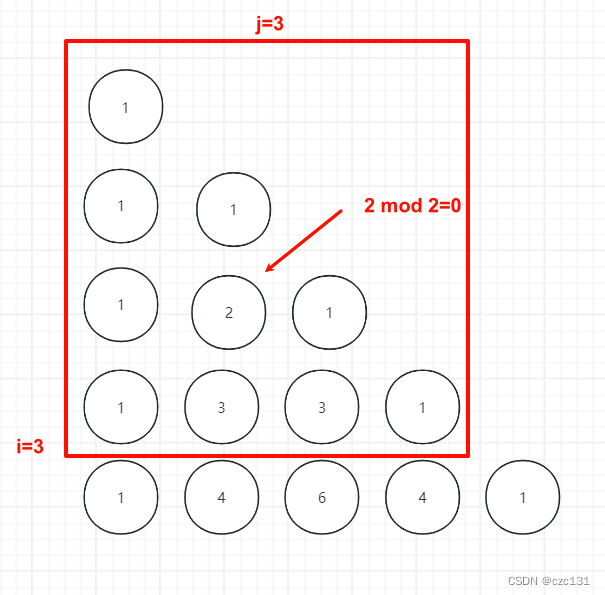
因为有多个询问,那么问题就转为了对于任意i和j,怎么快速计算矩形内满足的数量,读题可以发现, k是恒定的,所以可以预处理出所有(i,j)对应的结果。
定义sum[i][j]为i行到j的前缀和,f[i][j]为到i行到j列(不包括大于j列的)满足mod k=0的,也就是答案数组,那么f[i][j]=f[i-1][j]+sum[i][j]。
#include<stdio.h>
#include<algorithm>
using namespace std;
int tran[2024][2024];//记录杨辉三角
int f[2024][2024];//状态转移 //f[n][m]=f[n-1][m-1]+f[n-1][m]
int t,m,n,k;
int main()
{scanf("%d%d", &t,&k);int maxi = 2010;for (int i = 0; i < maxi; i++)tran[i][0] = 1;int j;for (int i = 1; i <= maxi; i++) {int sum_tmp = 0;//当前行的和for (j = 1; j <= i; j++) {//printf("(%d,%d)%d+%d,", i,j,tran[i - 1][j - 1], tran[i - 1][j]);tran[i][j] = (tran[i - 1][j - 1] + tran[i - 1][j])%k;// 因为后面反正也是要看是不是k的倍数的//printf("%d,", tran[i][j]);if (tran[i][j] == 0) {sum_tmp++;}f[i][j] = f[i - 1][j] + sum_tmp; // 计算数量//printf("(i=%d,j=%d)%d ",i,j, f[i][j]);}f[i][j] = f[i][j - 1];//这是为了下面一行的转移//printf("\n");}for (int epoch = 1; epoch <= t; epoch++) {scanf("%d%d", &n, &m);m = min(m, n);//printf("n=%d m=%d\n", n, m);printf("%d\n", f[n][m]);}return 0;
}分解质因数
Hankson 的趣味题
[NOIP2009 提高组] Hankson 的趣味题 - 洛谷
这一题要一个数x满足和a0的公约数是a1,和b0的最小公倍数是b1,求满足的x数量。
《趣味题》确实是很有趣味,不过前提是能做出来,一开始看到这种题目也是傻眼,完全无从下手。容易得出的是x=k1*a1=b1/k2(a1是公约数,b1是公倍数),因此k1*k2=b0/a0。
此时还需要知道的就是在什么时候k1和k2是合法的,可以证明若x=k1*a1,a0=k2*a1,此时gcd(k1,k2)=1,因为如果k1和k2还有公约数t,那么此时x和a0的最大公约数就应该是t*a1而不是a1,同理对于b的也是类似,因此可以得到判断条件,也就是系数之间的最大公约数都是1。枚举k1并计算出k2判断是否合法,统计出数量。
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
int gcd(int x, int y) {return y == 0 ? x : gcd(y, x%y); // 一句话搞定 这个相当于要是x>y那么就换个位置
}bool check(int x, int y) {if (gcd(x, y) == 1)return 1;return 0;
}int main()
{int t, a0, a1, b0, b1;scanf("%d", &t);int cnt;while (t--) {scanf("%d%d%d%d", &a0, &a1, &b0, &b1);// 开始枚举cnt = 0;int mul_k = b1 / a1;//printf("mul_k=%d\n", mul_k);//printf("%d\n", int(sqrt(mul_k)));int x;// a1是公约数,b1是公倍数for (int now = 1; now<= sqrt(mul_k); now++) { // x=k1*a1=b1/k2 这里枚举的是k1(防止迭代变量变化,这里使用now作为迭代变量)int k = now;if (mul_k%k)continue;// 判断k时的情况x = k * a1; // 算出xif (x%a1 == 0 && b1 % x == 0) { // 满足倍数和约数if (check(a0 / a1, k) && check(b1 / b0, mul_k / k)) {cnt++;}}if (k*k == mul_k) continue;//重复的不用再算一次// 判断mul_k/k时的情况k = mul_k / k;x = k * a1; // 算出xif (x%a1==0 || b1 % x==0) { // 满足倍数和约数if (check(a0 / a1, k) && check(b1 / b0, mul_k / k)) {cnt++;}}}printf("%d\n", cnt);}return 0;
}细胞分裂
[NOIP2009 普及组] 细胞分裂 - 洛谷
这一题需要计算的是一个数(细胞数)及其幂次是否可以为一个数(试管数)的倍数,涉及三个知识点。
- 一个大于2的数都可以分解为若干质数的乘积。
- 一个数是另一个数的倍数满足这个数的质数分解列表包含另一个数的质数分解列表。
- 幂次不改变质数列表的元素,只改变次数,假设m的分解包含t个x,那么m^n包含t*n哥x。
那么这题的思路就很简单了,就是先分解试管数量,再逐个分解细胞数,一个个计算结果找出最小的。
#include<stdio.h>
#include<math.h>
#include<algorithm>
#define N 30000
using namespace std;
struct PipeNode {int num;int idx; // 当前质因数idx有num个
}pipeNode[N+20];
struct Flags {int num; int x0; // 标记当前所属的初值(也就是每种细菌),每次分解质因数都要标记是属于哪种的,如果不匹配就是前面的,那么桶就不需要重复初始化
}flag[N+20]; // 下标就是质因数的数值
int n,m1,m2; // 细菌总数
int a[N+20];
int primes[N+1],prime_cnt;
int pipeCnt;// 试管质因数数量
bool check_prime(int x) {if (x % 2 == 0)return 0;for (int i = 3; i <= sqrt(x); i++) {if (x%i == 0)return 0;}return 1;
}int main()
{scanf("%d", &n);scanf("%d%d", &m1, &m2);for (int i = 1; i <= n; i++)scanf("%d", a + i);// 质因数打表primes[++prime_cnt] = 2;for (int i = 3; i <= N + 10; i++) {if (check_prime(i))primes[++prime_cnt] = i;}// 首先给试管做质因数分解if (m1 == 1) {printf("0\n");//一个就是初始数量,肯定可以满足return 0;}else {for (int i = 1; i <= prime_cnt; i++) {// 枚举质因数if (m1%primes[i] == 0) { // 如果可以分解pipeNode[++pipeCnt].idx = primes[i];pipeNode[pipeCnt].num = 0;while (m1%primes[i] == 0) {pipeNode[pipeCnt].num++;m1 /= primes[i];}}if (m1 == 1)break;//分解结束}}for (int i = 1; i <= pipeCnt; i++)pipeNode[i].num *= m2;// 质因数*倍数// 开始检查每种细菌int ans = 0x3f3f3f3f;//存储需要再过的最短时间for (int index = 1; index <= n; index++) {int x0 = a[index];//printf("a[index]=%d\n", a[index]);// 分解x0并装进桶里int x0_copy = x0;for (int i = 1; i <= prime_cnt; i++) {if (x0_copy%primes[i] == 0) {flag[primes[i]].x0 = x0;flag[primes[i]].num = 0;while (x0_copy%primes[i] == 0) {flag[primes[i]].num++;x0_copy /= primes[i];}}if (x0_copy == 1)break;}// 检查当前细菌是否可以达到菌均分int res = -1; // 找最大值,存在不符合要求的就是-1for (int i = 1; i <= pipeCnt; i++){ // 检查所有菌int num = pipeNode[i].num;int idx = pipeNode[i].idx;if (flag[idx].x0 != x0) {//x0当前没有质因数分解到idx(试管的某个质因数)res = -1;break;}int flag_num = flag[idx].num; // 菌初始值// 计算需要多长时间int det = max(0,num - flag_num);if (det) {res = max(res,(det - 1) / flag_num + 1);}else {res = max(res,0);}if (res > ans)break;//没必要算了}if (res != -1) {ans = min(ans, res);}if (ans == 0)break;//不用算了}if (ans == 0x3f3f3f3f) {printf("-1\n");}else {printf("%d\n", ans+1); // 初始时间为1}return 0;
}思维题
找筷子
找筷子 - 洛谷
这一题需要找到若干个数中,唯一的数量为奇数的那个数字,思路感觉比较巧妙,利用了异或的思路,因为一个数异或偶数次后为0,因此把全部数字取异或后就可以得到个数为奇数的那个数字。
一个数异或两次就是0可以查一下异或的定义,两次为0,那么异或偶数次都是0。
#include<stdio.h>
int main()
{int a=0,n,x;scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &x);a ^= x;// 取异或}printf("%d\n", a);return 0;
}
进制转换
[NOIP2000 提高组] 进制转换 - 洛谷
这一题涉及到了负进制的概念,比较新颖,一开始确实是没想到十进制数字转为负数进制的方法,后来查了一下,转为负进制也是使用短除法。
类似转为二进制一直除以2,最后从余数逆向连起来得到结果,对于负二进制,也是除以-2,但是直接用C语言的'%'符号计算是会得到负余数的,比如除数为3,转为-2进制,(-3)÷(-2)=1...-1(1余-1),此时为了让余数为非负,把余数的一个被除数放到商,也就是(-3)÷(-2)=2...1,此时2*(-2)+1=-3,然后继续2÷(-2)=-1...0...一直到最后商为1或者为0,那么可以结束(这里一时忘记当时怎么想的了,0结束好理解,1结束应该是因为再除也是一样的结果?)。
去掉前导0不要忘记。
#include<stdio.h>
int a,b;
int res[100000], cnt;
int main()
{scanf("%d%d", &a, &b);int a_copy = a;while (a != 1 && a != 0) {int div = a / b;int mod = a % b;//printf("div=%d mod=%d\n", div, mod);if (mod < 0) {mod -= b;div++;}res[++cnt] = mod;a = div;}if(a) res[++cnt] = a; // 最后一位是1保存下来,0就不要了printf("%d=", a_copy);for (int i = cnt; i >=1; i--) {if(res[i]<=9)printf("%d", res[i]);else printf("%c", 'A' + res[i] - 10);}printf("(base%d)", b);return 0;
}又是毕业季II
又是毕业季II - 洛谷
这一题要计算从n个数中任意取m(1≤m≤n)个数,分别对应的最大公约数。
这一题的思路有点巧妙,当然不是我想到的...
m越大,最大公约数越小,也就是选的越多,那么最大公约数一定越小(如果m个对应了更大的最大公约数,那么m-1个也能满足取得这个最大公约数,那么就矛盾了)。首先计算出每个数的所有因子(不是质因子),并给这些因子计数,然后从后往前看(后也就是公因数可能的最大值,也就是max(a[1~n]),也就是m=1对应的最大公约数),要是某个数字作为因子的个数恰好为m个,那么就是任选m个数字对应的最大公因数(这m个数就是对应此时最大公约数的选择方案,可以细品一下)
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
#define N 1000000
int n;
int flag[N + 10];
int main()
{scanf("%d", &n);int x;int maxx = -1;for (int i = 1; i <= n; i++) {scanf("%d", &x);maxx = max(x, maxx);// 分解所有质因数,存入flagfor (int j = 1; j < sqrt(x); j++) {if (x%j == 0) {flag[j]++;flag[x / j]++;}}int sqrt_x = sqrt(x); // 特判if (pow(sqrt_x,2) == x) {flag[sqrt_x]++;}}for (int i = 1; i <= n; i++) {while (flag[maxx] < i)maxx--;printf("%d\n", maxx); // 打印当前位置}return 0;
}这个题单其实还有一些没写,确实有点超出理解水平了,先记录到这里。