39. 组合总和
题目链接:组合总和
题目描述:
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
解题思路:
本题和昨天得组合题目只有略微不同,就是数字可以重复,因此我们每此递归就要改变原先的index值,从当前数字开始递归,这样就可以保证有重复数字,而怎么保证组合不同呢,就要靠将数组排序,从低到高得选择数字就可以保证不重复组合,每次至少一个不同,并可根据和大于target来剪支。
代码实现:
class Solution {List<List<Integer>> res = new ArrayList<>();int sum = 0;List<Integer> path = new ArrayList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates);backtracking(candidates,target,0);return res;}public void backtracking(int[] candidates, int target, int index) {if (sum == target) {res.add(new ArrayList(path));return;}for (int i = index; i < candidates.length; i++) {if (sum + candidates[i] > target) {break;}path.add(candidates[i]);sum += candidates[i];backtracking(candidates, target, i);sum -= candidates[i];path.remove(path.size() - 1);}}
}
40. 组合总和 II
题目链接:组合总和 II
题目描述:
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
解题思路:
跟上一题得区别在于给出得candidates中有重复元素,关键在于理解去重部分是在同一层数组中去重,而在一条路径下不去重,也就是for去重,递归不去重,因此去重操作应该在for循环内。
代码实现:
class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList<>();int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);backtraversal(candidates, target, 0);return res;}public void backtraversal(int[] candidates, int target, int index) {if (sum == target) {res.add(new ArrayList(path));return;}for (int i = index; i < candidates.length; i++) {if (i > index && candidates[i] == candidates[i - 1]) {continue;}if (sum + candidates[i] > target) {break;}sum += candidates[i];path.add(candidates[i]);backtraversal(candidates, target, i + 1);path.remove(path.size() - 1);sum -= candidates[i];}}
}
131. 分割回文串
题目链接:分割回文串
题目描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
解题思路:
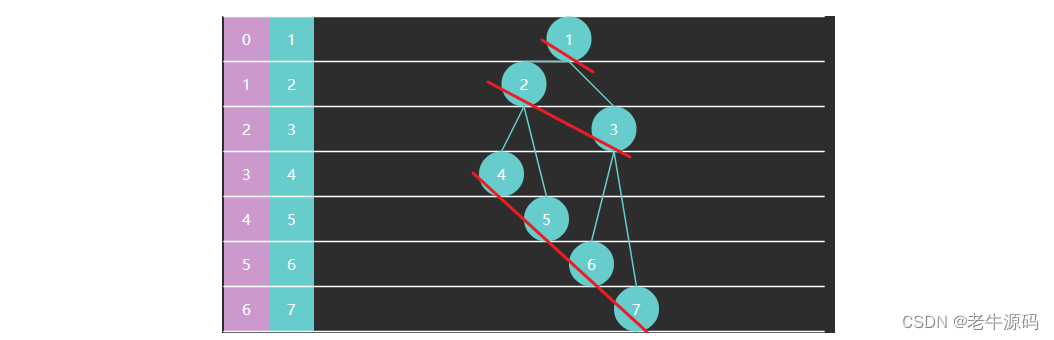
本题的整个思路如图按照这个进行同层遍历和递归遍历即可,难度不大,关键点在于判断是否是回文串,最简单得方法就是采用双指针,一前一后依次比对得判断相等否。还有一种方法是利用动态规划: 具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。所以根据这个可以定义一个预处理二维布尔数组来对s中的子串进行预处理
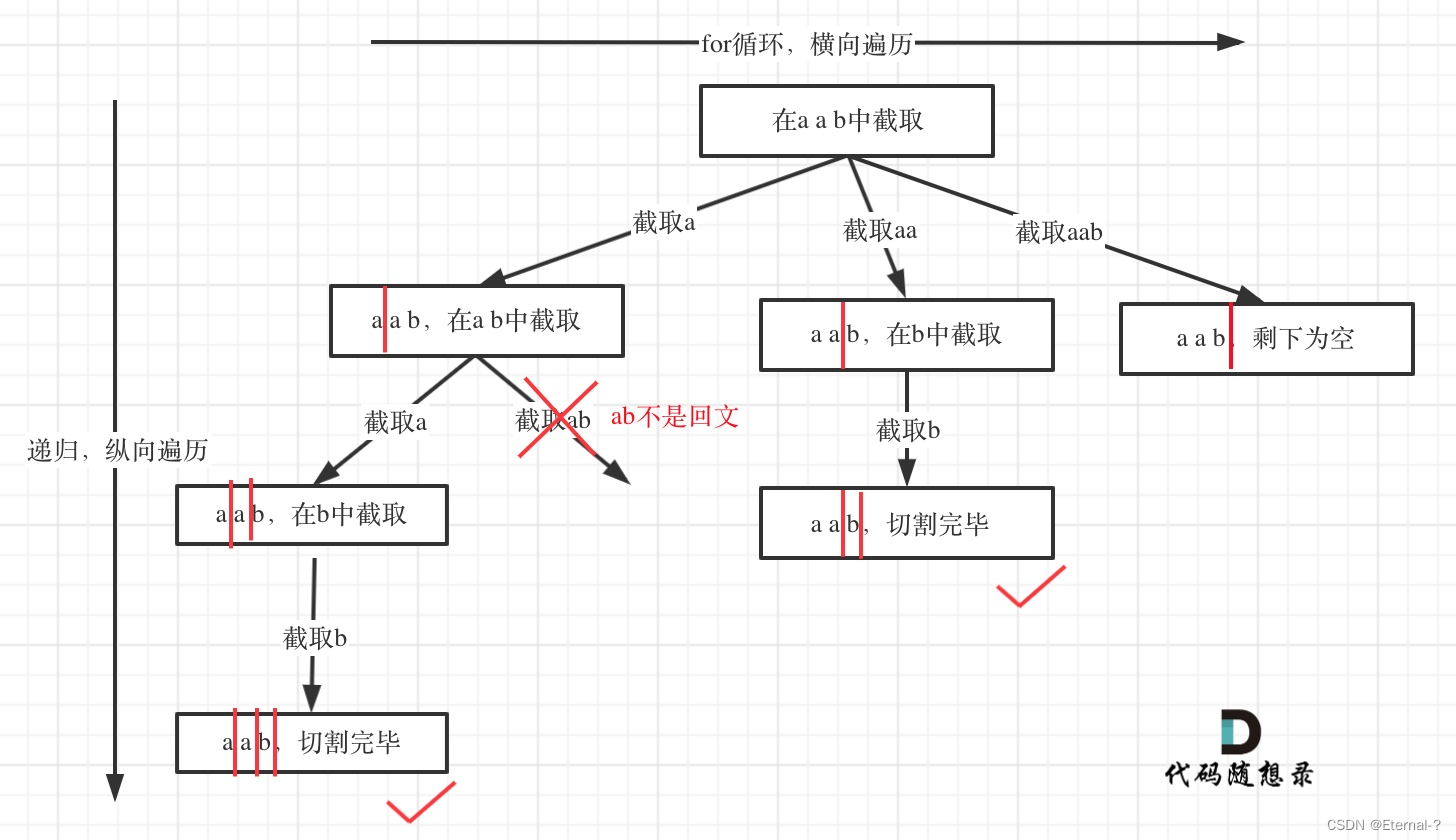
代码实现:
class Solution {List<List<String>> res = new ArrayList<>();Deque<String> deque = new LinkedList<>();public List<List<String>> partition(String s) {backtraversal(s, 0);return res;}public void backtraversal(String s, int index) {if (index == s.length()) {res.add(new ArrayList(deque));return;}for (int i = index; i < s.length(); i++) {if (isPalindrome(s, index, i)) {String str = s.substring(index, i + 1);deque.addLast(str);} else {continue;}backtraversal(s, i + 1);deque.removeLast();}}private boolean isPalindrome(String s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;}
}
动态规划判断回文字符串
class Solution {List<List<String>> res = new ArrayList<>();Deque<String> deque = new LinkedList<>();boolean[][] f;public List<List<String>> partition(String s) {f = new boolean[s.length()][s.length()];for (int i = s.length()-1; i >=0; i--) {for (int j = i; j < s.length(); j++) {if(i==j){f[i][j]=true;}else if(j - i == 1&&s.charAt(i)==s.charAt(j)){f[i][j]=true;}else if (s.charAt(i) == s.charAt(j) &&f[i + 1][j - 1]) {f[i][j] = true;} else {f[i][j] = false;}}}backtraversal(s, 0);return res;}public void backtraversal(String s, int index) {if (index == s.length()) {res.add(new ArrayList(deque));return;}for (int i = index; i < s.length(); i++) {if (f[index][i]) {String str = s.substring(index, i + 1);deque.addLast(str);} else {continue;}backtraversal(s, i + 1);deque.removeLast();}}
}