笔记---贪心---排序不等式，绝对值不等式-编程知识

笔记---贪心---排序不等式，绝对值不等式

排序不等式 AcWing.913.排队打水

有 $n$ 个人排队到 $1$ 个水龙头处打水，第 $i$ 个人装满水桶所需的时间是 $t_{i}$ ，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式
第一行包含整数 $n$ 。

第二行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 个人装满水桶所花费的时间 $t_{i}$ 。

输出格式
输出一个整数，表示最小的等待时间之和。

数据范围
$1≤n≤10^{5},$
$1≤t_{i}≤10^{4}$

输入样例：

7
3 6 1 4 2 5 7

输出样例：

显然，所有人等待的总时间就是 $t_{1} * (n - 1) + t_{2} * (n - 2) + ... + t_{n-1} * 1$

那么从小到大排序进行排队可以得到最短的时间

#include<iostream>
#include<algorithm>
using namespace std;const int N = 100010;int n;
int t[N];int main() {cin >> n;for (int i = 0; i < n; i++)cin >> t[i];sort(t, t + n);long long res = 0;for (int i = 0; i < n; i++)res += t[i] * (n - i - 1);//公式cout << res;return 0;
}

绝对值不等式 AcWing.104.货仓选址

在一条数轴上有 $N$ 家商店，它们的坐标分别为 $A_{1}∼A_{N}$ 。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式
第一行输入整数 $N$ 。

第二行 $N$ 个整数 $A_{1}∼A_{N}$ 。

输出格式
输出一个整数，表示距离之和的最小值。

数据范围
$1 \leq N \leq 100000,$
$0≤A_{i}≤40000$

输入样例：

4
6 2 9 1

输出样例：

设 $x$ 是货仓的坐标， $x_{i}$ 是商店的坐标
根据题意，我们要求 $f(x) = |x_{1} - x| + |x_{2} - x| + |x_{3} - x| + ...... + |x_{n} - x|$ 的最小值
之后将其分组：
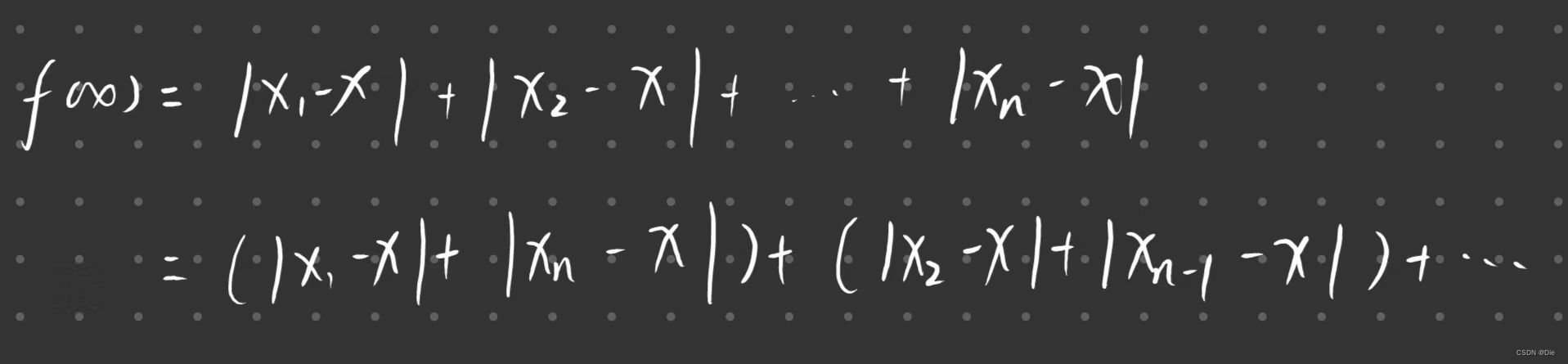
在这里插入图片描述

其中 $x_{1} - x| + |x_{n} - x|$ 代表的就是货仓到达两个商店的距离，这个距离可能有以下情况：

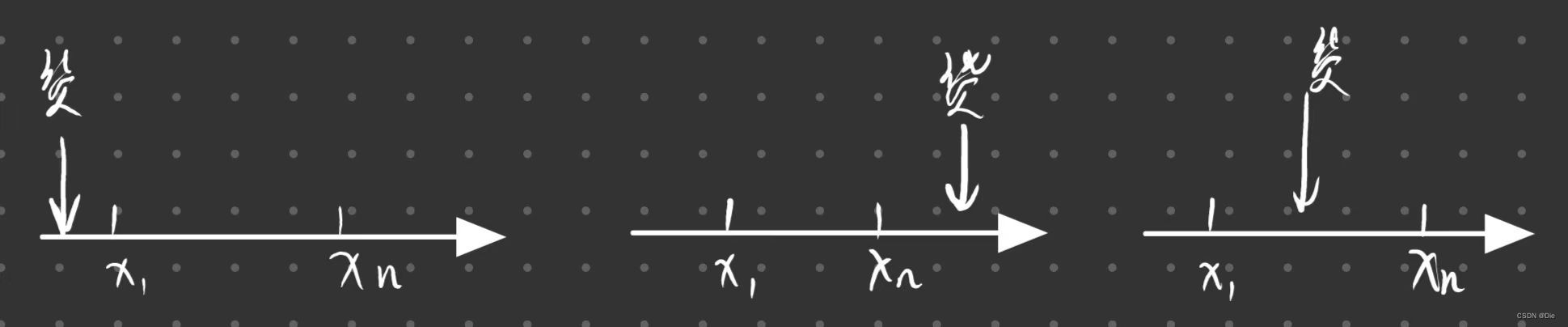
在这里插入图片描述

很明显，只有第三种情况才是距离最小的情况，这时的距离可以表示为： $x_{n} - x_{1}|$

所以这个式子可以写成 $f(x) >= x_{n} - x_{1} + x_{n-1} - x_{2} + ......$
那么接下来的问题就是证明等号能否成立

要整个式子满足等号，那么就应该让每一组式子满足等号
想让第一组式子等号满足( $x_{n} - x| + |x_{1} - x| = x_{n} - x_{1}$ )的条件是货仓落在 $x_{n}$ 和 $x_{1}$ 之间，同理得所有组式子也同样要满足这个要求，则当所有条件都满足时，就可以让整个式子取得等号

如果为奇数的情况下，可以使货仓偏向一边

详细证明：AcWing算法基础课贪心（二）00:30:00

代码：

#include<iostream>
#include<algorithm>using namespace std;const int N = 100010;int n;
int a[N];int main() {cin >> n;for (int i = 0; i < n; i++)cin >> a[i];sort(a,a+n);int res = 0;for (int i = 0; i < n; i++)res += abs(a[i] - a[n/2]);//枚举并减中位数，即算出总距离cout << res;return 0;
}