14 归并排序和其他排序-编程知识

1.归并排序
2.计数排序

1. 归并排序

基本思想

建立在归并操作上的一种排序算法,采用分治法的一个典型应用。将已有序的子序列合并，得到完全有序的序列，将两个有序表合成一个称为二路归并。
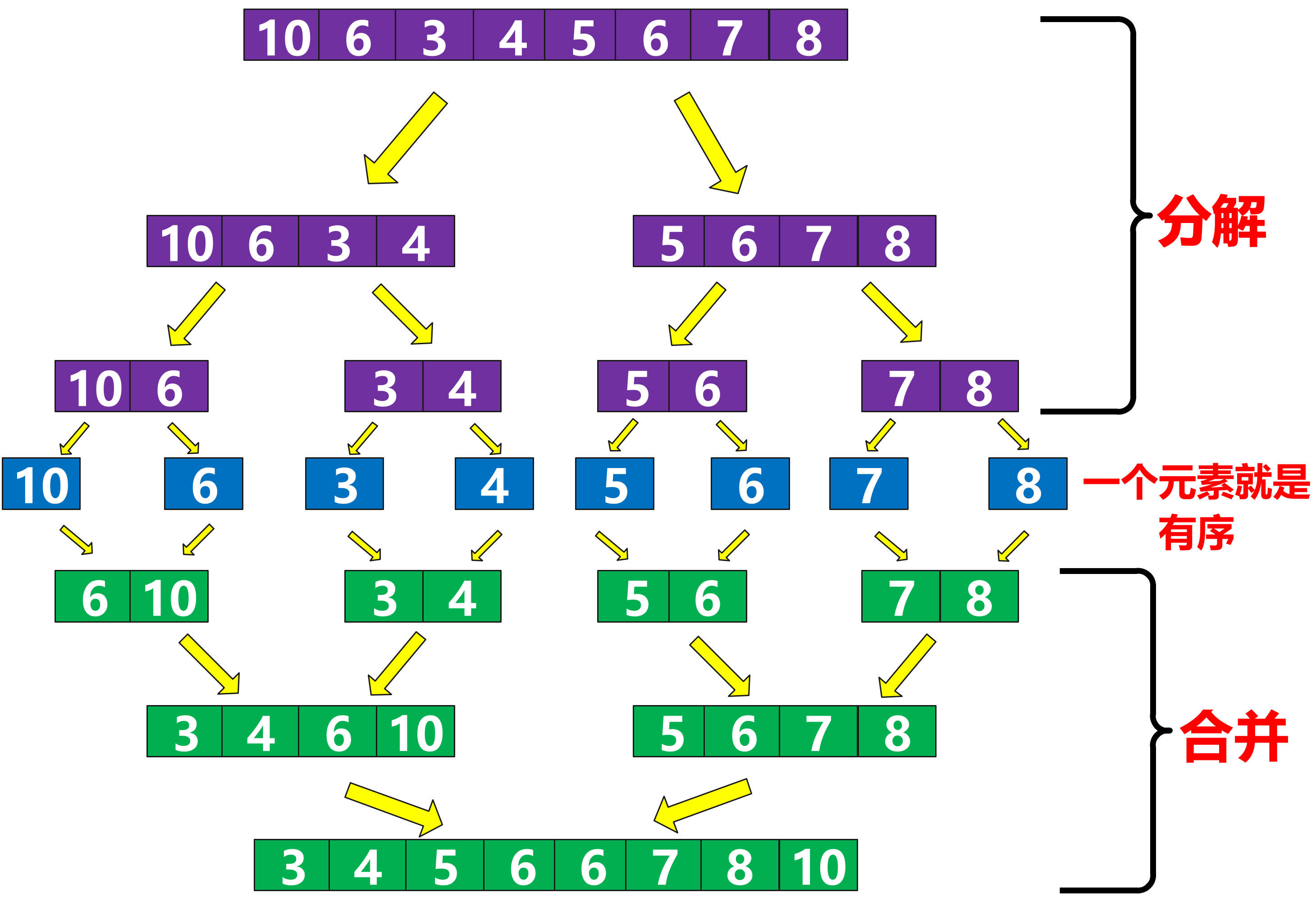
在这里插入图片描述

原数组无序，以中间分割为两个数组，仍然无序，继续分割每个区间，直到两个数时，可以使它有序，然后利用两个数组的合并，将小的尾插，不断的就可以排序之前分割的完整序列。采用的类似后序的方法，想要让原数组有序，只需要让它的左右区间有序，再对原数组做有序处理

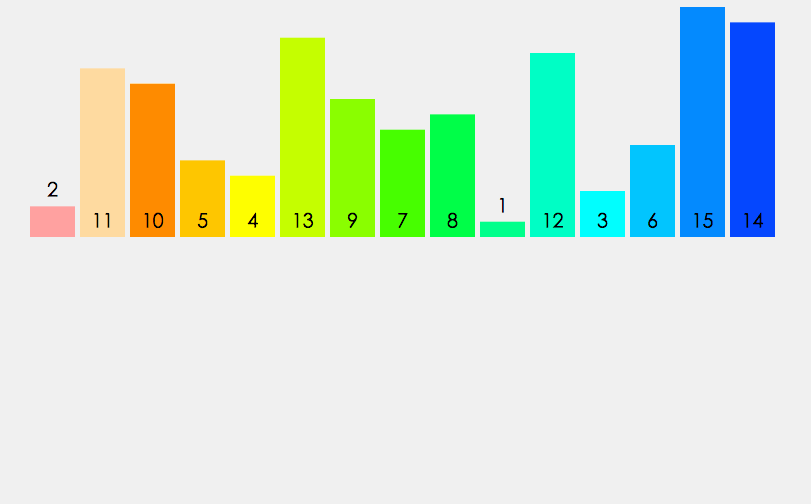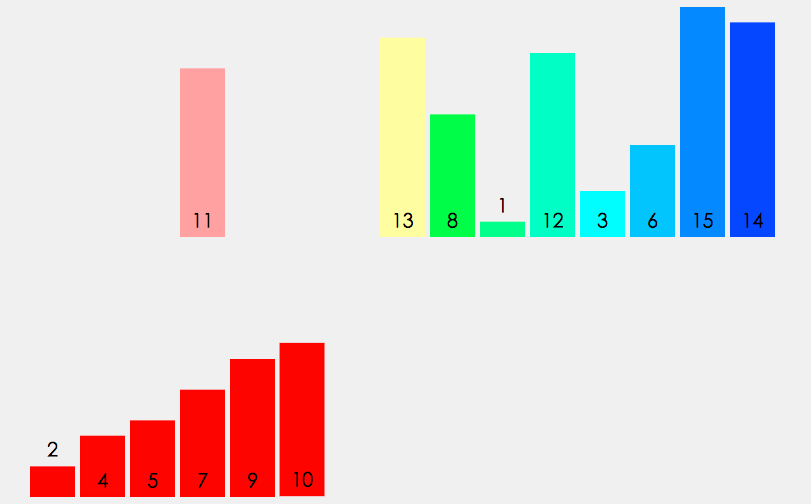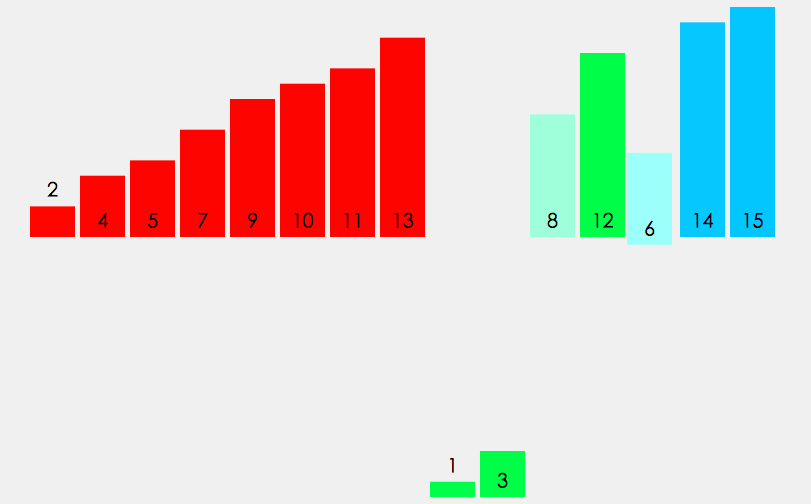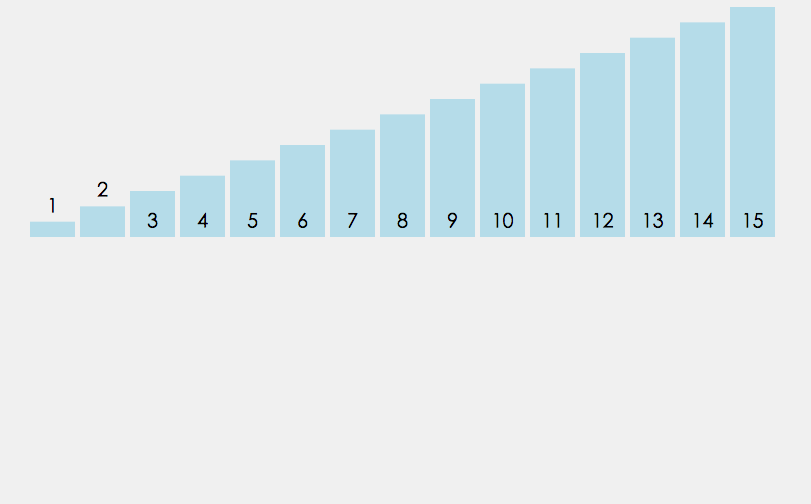
在这里插入图片描述

因为需要对每组数据排序，需要申请一段和原数组一样的空间，在原数组直接排序会覆盖需要的数据。申请空间的部分需要和递归部分分开写。取中间变量对原数组分割的左右区间做递归，用四个变量记录两个左右区间的范围，当两端区间都存在的时候合并两个区间，最后拷贝回原数组，区间不存在返回

递归

void _MergeSort(int ary[],int begin, int end, int temp[])
{//终止条件,不存在大于区间if (begin == end){return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]//递归循环_MergeSort(ary, begin, mid, temp);_MergeSort(ary, mid+1, end, temp);//定义边界int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;//下标int i = begin;while (begin1 <= end1 && begin2 <= end2){if (ary[begin1] <= ary[begin2]){temp[i++] = ary[begin1++];}else{temp[i++] = ary[begin2++];}}//没放完的while (begin1 <= end1){temp[i++] = ary[begin1++];}while (begin2 <= end2){temp[i++] = ary[begin2++];}//拷贝回去,加1memcpy(ary+begin, temp+begin, sizeof(int) * (end - begin + 1) );
}
//归并排序
void MergeSort(int ary[], int len)
{int* temp = (int*)malloc(sizeof(int) * len);_MergeSort(ary, 0, len -1 , temp);
}

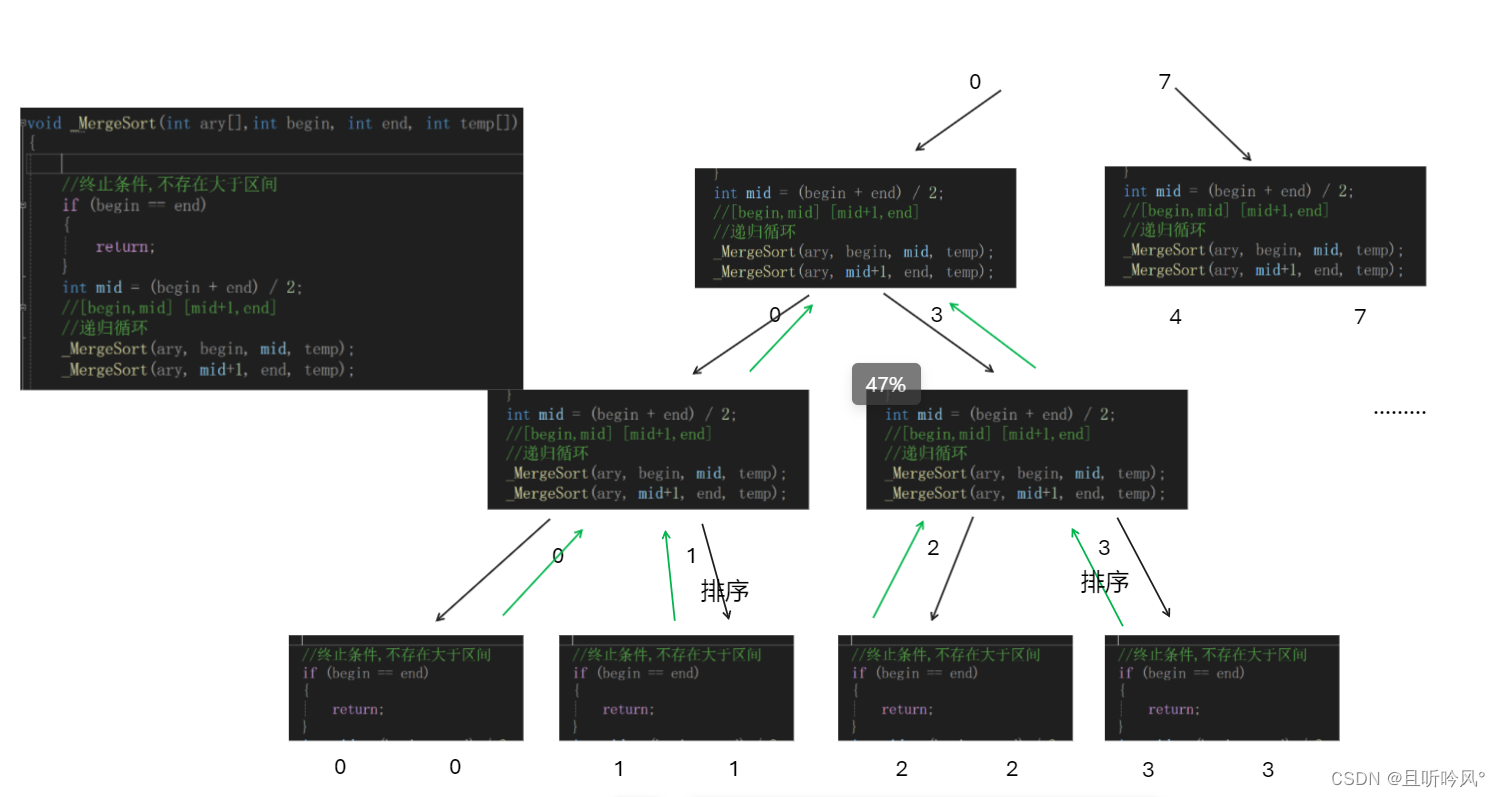
左边区间递归情况
在这里插入图片描述
循环
循环需要以gap作为变量，控制每组的数量。每个for循环对这gap的分组进行排序，模仿递归从最后一层往回走的过程。先把左右分组排好序，再合并排序。不能使用栈的原因是，栈排好后数据会销毁，合并的时候不知道合并的两个区间是什么

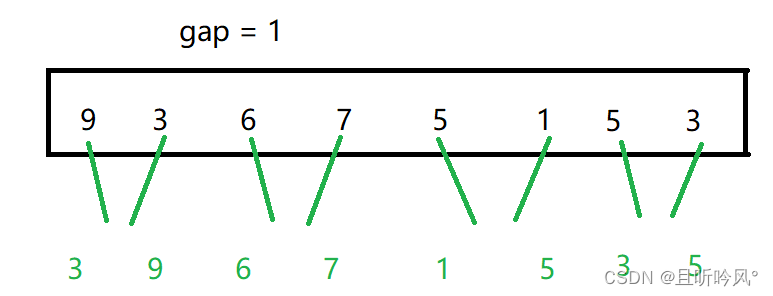
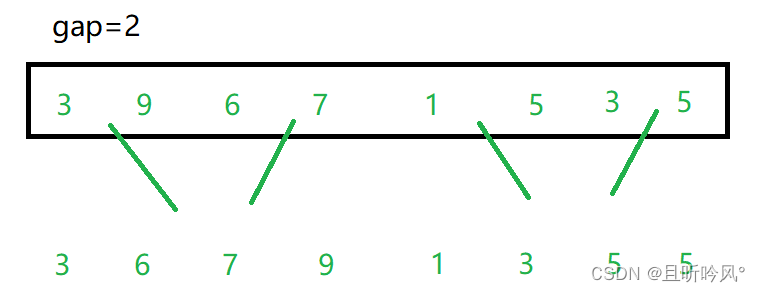
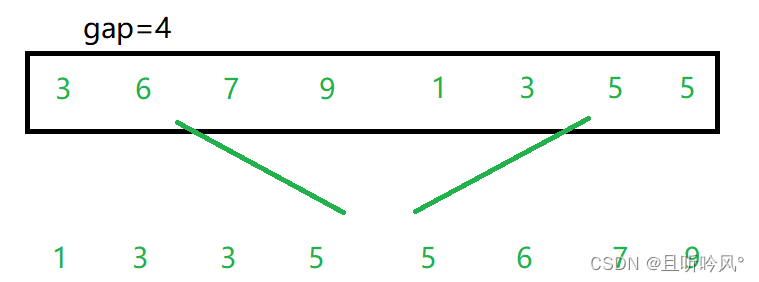
在这里插入图片描述

其中，需要关注的是分组的越界情况。可能有3个越界
1.end1,begin2,end2全部越界
2.begin2,end2越界
3.end2越界

//归并排序 循环
void Mergesort(int ary[], int len)
{int* temp = (int*)malloc(sizeof(int) * len);//gap归的数量int gap = 1;while (gap < len){//下标int j = 0;for (int i = 0; i < len; i += 2 * gap){//每组合并int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//打印左右区间//printf("[%d,%d],[%d,%d]\r\n", begin1, end1, begin2, end2);//对于超过数组范围的区间调整//end1,begin2超过直接break//edn2超过修改end2if (end1 >= len || begin2 >= len){break;}if (end2 >= len){end2 = len - 1;}while (begin1 <= end1 && begin2 <= end2){if (ary[begin1] <= ary[begin2]){temp[j++] = ary[begin1++];}else{temp[j++] = ary[begin2++];}}//没放完的while (begin1 <= end1){temp[j++] = ary[begin1++];}while (begin2 <= end2){temp[j++] = ary[begin2++];}//归并一组,拷贝一组memcpy(ary + i, temp + i, sizeof(int) * (end2 - i + 1));}//整体拷贝回去//memcpy(ary, temp, sizeof(int) * len);gap = gap * 2;//printf("\r\n");}}

优化
归并法假如有很大的数据量，分割成比较小的组里，如果再继续分下去，就没有必要，浪费效率。所以对于比较小的组可以直接采用另一种排序的方法来排序。叫小区间优化，如果指定数量用另一种排序效率高于归并，就说明优化是有效的

void _MergeSort(int ary[],int begin, int end, int temp[])
{//终止条件,不存在大于区间if (begin == end){return;}//只剩10个,可以用其他排序提升效率//小区间优化if ((end - begin + 1) < 10){Sort(ary + begin, end - begin + 1);return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]//递归循环_MergeSort(ary, begin, mid, temp);_MergeSort(ary, mid+1, end, temp);//定义边界int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;//下标int i = begin;while (begin1 <= end1 && begin2 <= end2){if (ary[begin1] <= ary[begin2]){temp[i++] = ary[begin1++];}else{temp[i++] = ary[begin2++];}}//没放完的while (begin1 <= end1){temp[i++] = ary[begin1++];}while (begin2 <= end2){temp[i++] = ary[begin2++];}//拷贝回去,加1memcpy(ary+begin, temp+begin, sizeof(int) * (end - begin + 1) );
}

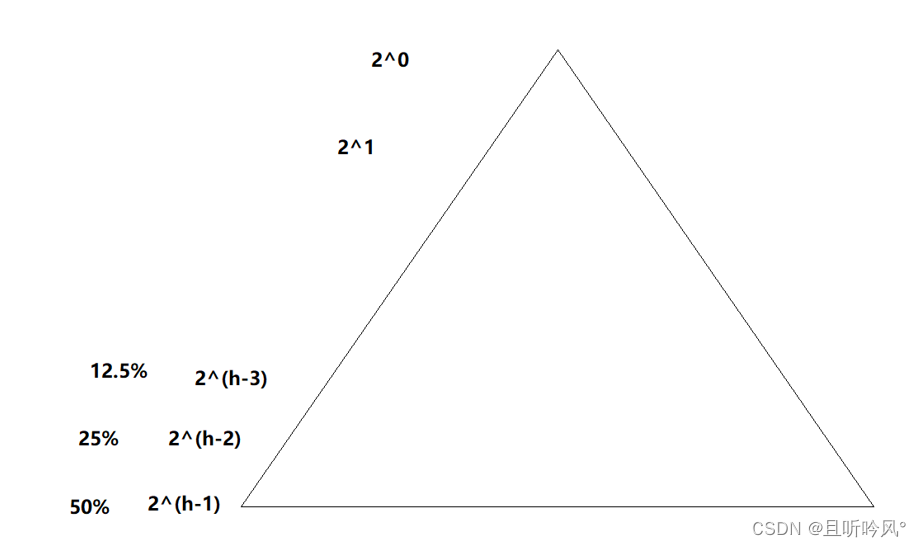
在这里插入图片描述
上面是递归数量的展开图，倒数三层就占了总共87.5%的调用层次，所以小区间优化针对最下面的递归层次减少是有必要的

特性
1.归并的缺点在于O(N)的空间复杂度,更多的是解决磁盘中的外排序问题
2.时间复杂度: O(N*logN)
3. 空间复杂度: O(N)
4.稳定性: 稳定

2. 非比较排序

基本思想
计数排序又称鸽巢原理，是对哈希直接定址法的变形应用。操作步骤：

1.统计相同元素出现次数
2.根据统计的结果序列回收到原来的序列中

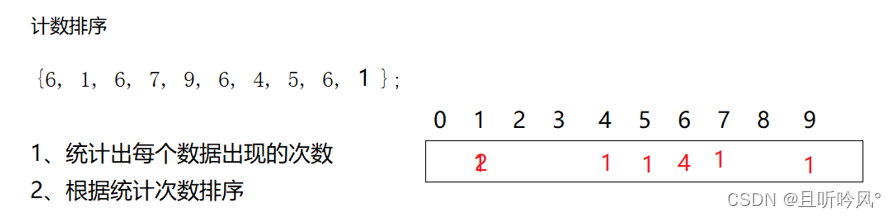
在这里插入图片描述

重新开一个数组，用这个数组来统计每个数出现的次数，比如上面的1出现了两次，就在下标1的位置填入2。如果原序列不是从0开始，那记录次数的数组0下标就不是记录0的次数了，用相对映射，如果数据最小值是100，那第一个下标处就记录100出现的次数，依次递增

//计数排序
void CountSort(int ary[], int len)
{//遍历找到序列最大和最小值int max = ary[0];int min = ary[0];for (int i = 0; i < len; i++){if (ary[i] > max){max = ary[i];}if (ary[i] < min){min = ary[i];}}//申请空间int range = max - min + 1;//数据初始化0int* temp = (int*)calloc(sizeof(int), range);//记录次数for (int i = 0; i < len; i++){temp[ary[i] - min]++;}//遍历数组int j = 0;for (int i = 0; i < range; i++){while (temp[i]--){//写回原序列ary[j++] = i + min;}}
}