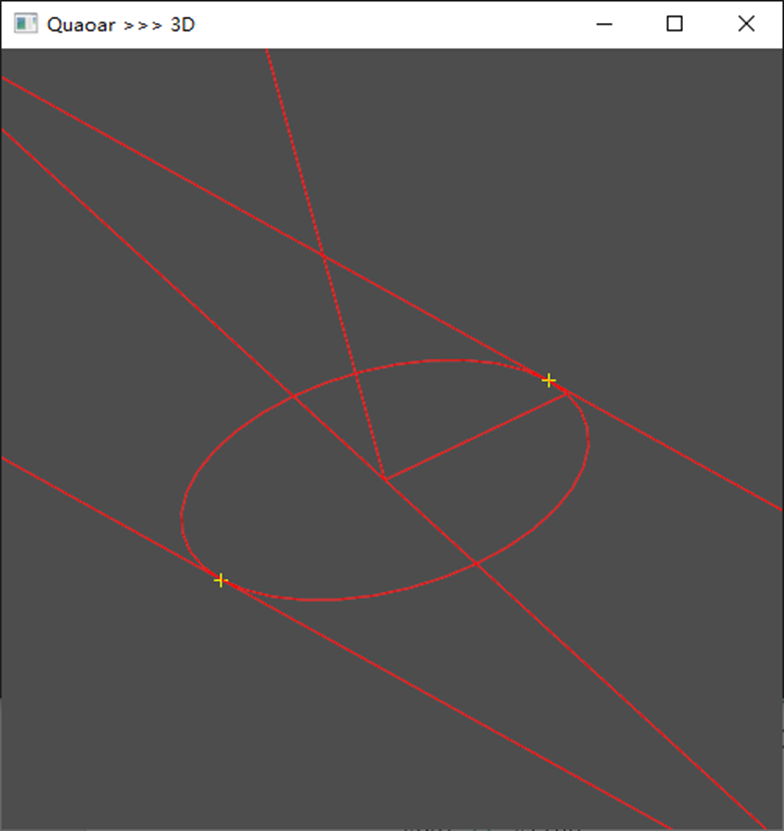
在几何学中,一个圆的切线被定义为与圆相切于一点的直线,而该点被称为切点。这意味着切线在切点处与圆仅有一个交点,并且在该点处,切线的方向与圆的半径垂直。
以下是关于圆的切线和切点的一些重要性质:
切线与半径的垂直性:在切点处,切线与通过该点的半径垂直。这是圆的切线最基本的性质,也是它得名的原因。
切点的唯一性:对于给定的圆和一条不在圆上的直线,它们最多只有一个切点。换句话说,一条直线不能与一个圆在多于一个点处相切。
切点在半径上的位置:切点到圆心的连线(即半径)与切线垂直。这是由切线与半径的垂直性直接得出的。
在解决与圆的切线相关的问题时,通常会用到这些性质。例如,要证明一条直线是圆的切线,可以通过证明该直线与圆在一点处相切,并且在该点处与半径垂直来实现。
此外,还有一些与圆的切线相关的定理和公式,如切线长定理等,这些都可以在解决几何问题时提供帮助。
下面,给出一个基于OCCT求解圆的切线与切点的例子:
#include <gp_Lin2d.hxx>
#include <GccEnt_QualifiedCirc.hxx>
#include <Geom2d_Circle.hxx>
#include <BRepBuilderAPI_MakeWire.hxx>
#include <BRepBuilderAPI_MakeVertex.hxx>
#include <gp_Ax2.hxx>
#include <BRepBuilderAPI_MakeEdge2d.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <GccEnt.hxx>
#include <gp_Circ.hxx>
#include"Viewer.h"
#include <GccAna_Lin2dTanObl.hxx>
#include <TColgp_Array1OfLin2d.hxx>
int main(int argc, char* argv[])
{gp_Dir Z(0.0, 0.0, 1.0);gp_Pnt center(0, 0, 0.0);gp_Pnt xr(0.5, 0, 0.0);gp_Pnt yr(0.0, 1.0, 0.0);gp_Pnt zr(0.0, 0.0, 7.0);gp_Ax2 wb(center, Z);gp_Circ wbcircle(wb, 0.125 / 2);TopoDS_Edge wbe = BRepBuilderAPI_MakeEdge(wbcircle);TopoDS_Edge xline = BRepBuilderAPI_MakeEdge(center, xr);TopoDS_Edge yline = BRepBuilderAPI_MakeEdge(center, yr);TopoDS_Edge zline = BRepBuilderAPI_MakeEdge(center, zr);//GccAna_Lin2dTanObl//首先创建一个二维空间的圆//gp::OX2d()为X轴,1.0为圆的半径,以X轴的原点作为圆心,创建一个二维圆gp_Circ2d c(gp::OX2d(), 1.0);TopoDS_Edge ec = BRepBuilderAPI_MakeEdge2d(c);//创建一条二维直线,与X轴重合gp_Lin2d theLine(gp::OX2d());TopoDS_Edge el = BRepBuilderAPI_MakeEdge2d(theLine);//声明两个数组,可以存储生成的切线tanLine和切点tanP,索引为1~2TColgp_Array1OfLin2d tanLine(1, 2);TColgp_Array1OfPnt2d tanP(1, 2);//solver用于生成一条直线,该直线与圆c相切,并且与theLine成10度的夹角Standard_Real ang = 10;GccAna_Lin2dTanObl solver(GccEnt::Unqualified(c), theLine, ang / 180 * 3.1415926); //注意:该构造函数中角度单位为弧度//计算成功时,solver.IsDone() 为True,solver.NbSolutions()返回结果的个数if (solver.IsDone() && solver.NbSolutions() > 0){for (Standard_Integer i = 1; i <= 2; i++){// solver.ThisSolution(i)返回计算得到的直线gp_Lin2d类型,i为结果的索引,范围1~2tanLine(i) = solver.ThisSolution(i);Standard_Real ParSol;Standard_Real ParArg;//solver.Tangency1()用于计算切点,tanP为切点solver.Tangency1(i, ParSol, ParArg, tanP(i));}}TopoDS_Vertex TVl = BRepBuilderAPI_MakeVertex(gp_Pnt(tanP(1).X(), tanP(1).Y(),0.0 ));TopoDS_Vertex TV2 = BRepBuilderAPI_MakeVertex(gp_Pnt(tanP(2).X(), tanP(2).Y(), 0.0));TopoDS_Edge TL1 = BRepBuilderAPI_MakeEdge2d(tanLine(1));TopoDS_Edge TL2 = BRepBuilderAPI_MakeEdge2d(tanLine(2));Viewer vout(50, 50, 500, 500);vout << xline;vout << yline;vout << zline;vout << ec;vout << el;vout << TVl;vout << TV2;vout << TL1;vout << TL2;vout.StartMessageLoop();return 0;
}