基于辛几何的分析方法是一种保护相空间几何结构的新型分析方法,主要用于求解动力学和控制系统中矩阵或Hamilton矩阵的特征值问题,用来解决在动力学和控制系统理论的2n×2n矩阵或哈密顿矩阵的特征值问题,已应用到结构损伤信号、奇异微分方程等系统中。辛几何谱分析SGSA是基于辛几何的一种分析方法,在非线性信号的降噪分析中具有独特优势。
辛几何模态分解SGMD是在辛几何分析的基础上一种新的信号分解方法,其利用辛几何相似变换求解Hamilton矩阵特征值,并利用相应的特征向量重建单分量——辛几何分量SGC,具有时间序列本质特征不变、抑制模态混淆等特点,可以在有效地重构单分量的过程中去除噪声,且无需定义任何主观参数。
本代码以能量消耗数据为例,采用辛几何模态分解SGMD对其进行分解,所用模块如下:
import numpy as np
import matplotlib.pyplot as plt
import scipy.linalg as lg
import pandas as pd部分代码如下:
if __name__ == '__main__':data_df = pd.read_excel('Energy Consumption.xlsx')columns_name = ['Energy Consumption']Data = pd.DataFrame(data_df, columns=columns_name)Data=np.array(Data).flatten()fs = 1sig=Datanfft = 50sgmd = SGMD(sig,fs,nfft=nfft,threshold_corr=0.8,threshold_nmse=0.001,mode='eig')SGCs = sgmd.sgmd()plt.rc('font',family='Times New Roman',size='12')# plt.figure()# plt.title('signals')# plt.subplot(4,1,1)# plt.plot(sig)# plt.xlim(0,len(sig))# plt.xlim([0,fs*t[-1]])# plt.subplot(4,1,2)# plt.plot(x1_t)# plt.xlim([0,fs*t[-1]])# plt.subplot(4,1,3)# plt.plot(x2_t)# plt.xlim([0,fs*t[-1]])# plt.subplot(4,1,4)# plt.plot(x3_t)# plt.xlim([0,fs*t[-1]])plt.figure()plt.title('SGCs From SGMD')for i in range(SGCs.shape[0]):plt.subplot(int(SGCs.shape[0]),1,i+1)plt.plot(SGCs[i])plt.title('SGC' + str(i))plt.xlabel('time')plt.ylabel('amplitude')plt.show()
df=pd.DataFrame(SGCs)
df.to_excel('SGC.xlsx')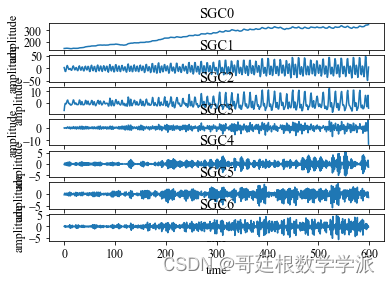
工学博士,担任《Mechanical System and Signal Processing》审稿专家,担任
《中国电机工程学报》优秀审稿专家,《控制与决策》,《系统工程与电子技术》,《电力系统保护与控制》,《宇航学报》等EI期刊审稿专家。
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。