- 难度: 困难
- 通过率: 29.6%
- 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。

以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
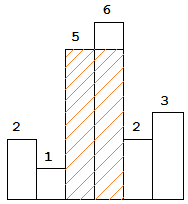
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3] 输出: 10
分析
对于每根柱子,尝试以该柱子的高度作为构成的矩阵的高,向两边扩张,直到遇到比当前柱子矮的。如此,就得到了宽度,进而得到面积。这种方法是时间复杂度为 。
如果柱子的按高度递增的顺序排列,对于每个柱子,以它作为矩形高度,矩形的宽度就是右边的柱子数量。因为右边的目标,肯定比该柱子要高。基于此想法,维护一个单调递增栈,在遇到一个比栈顶木板短的木板时,栈中的所有柱子就是递增排列的。只是这些柱子不一定是挨在一起的。因此需 基于下标得出矩形的宽度。
解法:单调栈
class Solution {public:int largestRectangleArea(vector<int> &heights) {stack<int> stk;int area = 0;stk.push(-1);for (int i = 0; i <= heights.size(); i++) {int curr = i < heights.size() ? heights[i] : 0;while (stk.top() != -1 && curr < heights[stk.top()]) {int height = heights[stk.top()];stk.pop();int width = i - stk.top() - 1;area = max(area, height * width);}stk.push(i);}return area;}
};
![[word] word表格表头怎么取消重复出现? #媒体#笔记#职场发展](https://img-blog.csdnimg.cn/img_convert/e904d5f845971483eca5c5db02c873eb.gif)