数据结构 - 线段树-编程知识

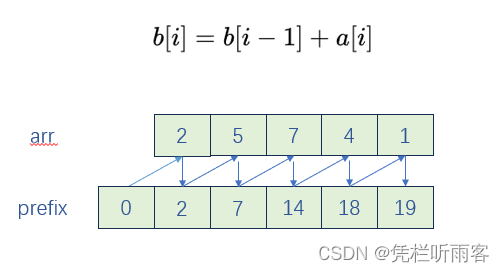
1. 预制值：

构建的数组为，nums：【2， 5， 1， 4， 3】
区间和问题，假设求区间 [1，3] 的和

2. 建树

2.1 构建线段树数组

int[] segT = new int[4*n]

（为什么数组大小是4*n？？？评论区欢迎留言）
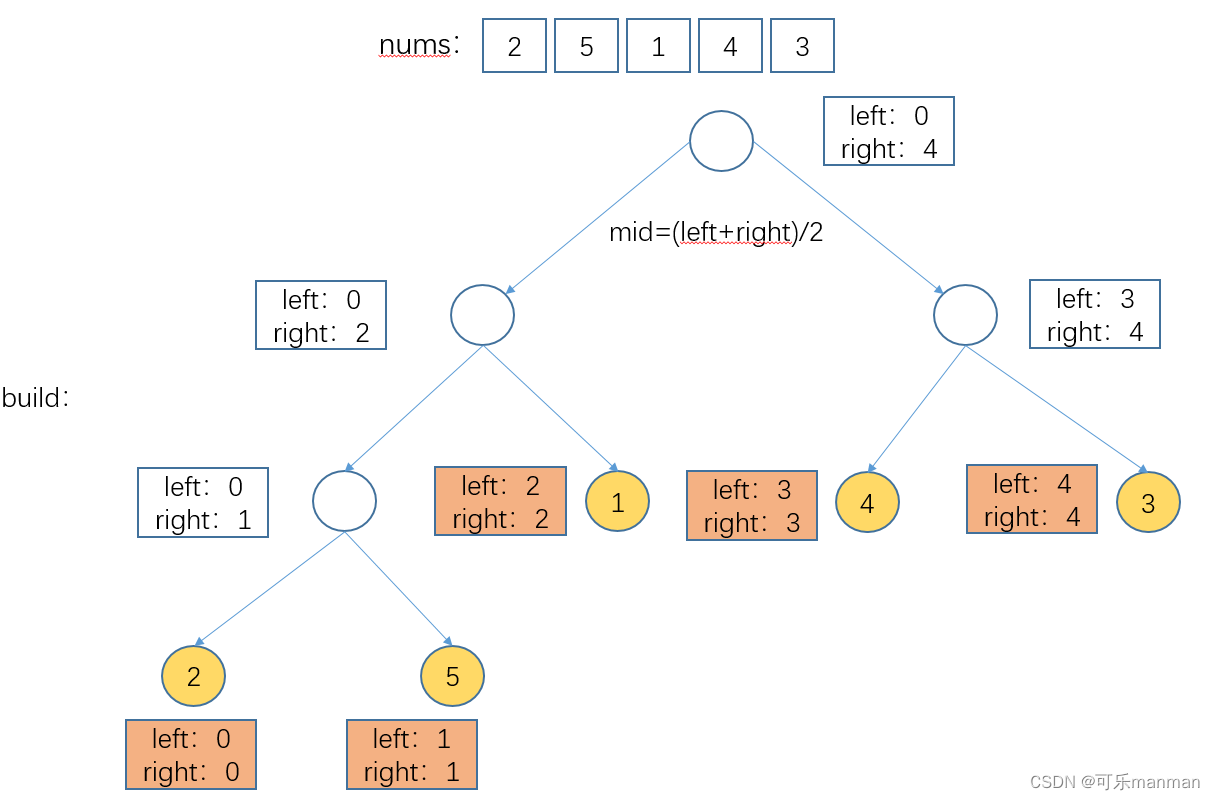
在这里插入图片描述

tips：长方格中的left、right，分别代表该节点所求得的区间和。例如，left：0，right：4。代表nums中索引0到4的和=2+5+1+4+3=15。

怎么构建线段树呢？
- 2.1.1 多次二分，一直切分每个大区间，知道left=right的时候，区间不可再切，此时填入nums[index]的值
- 2.1.2 得到不可再分区间，递归返回，根节点求和

核心代码

public void build(int index, int left, int right) {// 2.1.1的工作，递归条件，不可再分区间if (left == right) {segT[index] = nums[left];return;}// 2.1.1的工作，区间多次二分int mid = (right - left) / 2 + left;// 左子树根节点的索引int leftIndex = index * 2;// 右子树根节点的索引int rightIndex= index * 2 + 1;// 构建左、右子树build(leftIndex, left, mid);build(rightIndex, mid+1, right);// 2.1.2的工作，求根节点的和// tips：只有当left==right返回后，才会走这一步segT[index] = segT[leftIndex] + segT[rightIndex];}

3. 更新

逻辑其实和建树一样，在线段树中找到修改节点的对应索引，然后修改其值，然后再依次修改根节点的值即可。
在这里插入图片描述

核心代码

public void update(int index, int start, int end, int updateIndex, int value) {// 找到叶子节点，直接修改值（不可再分区间了）if (start == end) {nums[updateIndex] = value;segT[index] = value;return;} int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;// 修改的节点再左子树还是右子树if (updateIndex >= start && updateIndex <= mid) {update(leftIndex, start, mid, updateIndex, value);} else {update(rightIndex, mid + 1, end, updateIndex, value);}segT[index] = segT[leftIndex] + segT[rightIndex];}

4. 查询

查询的逻辑会稍微复杂一点，因为有三个因素：

4.1 查询的范围全落在左子树

在这里插入图片描述

4.2 查询的范围全落在右子树

在这里插入图片描述

4.3 查询的范围既在左子树、又在右子树

在这里插入图片描述

核心代码

public int querySum(int index, int start, int end, int left, int right) {// 查询的索引无效（不是线段树的有意义范围）if (left > end || right < start) {return 0;}// 查询的范围包含该子树的范围，直接返回即可（见下图【包含子树】）else if (left <= start && right >= end) {return st[index].sum;}// 求的左右子树的索引int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;// 左、右子树求得的值int leftSum = querySum(leftIndex, start, mid, left, right);int rightSum = querySum(rightIndex, mid + 1, end, left, right);return leftSum + rightSum;}

在这里插入图片描述
图：包含子树

5. 线段树求区间问题模板（最大值、最小值、和）

public class SegmentTree {class Node {int left;int right;int max;int min;int sum;Node() {}Node (int left, int right) {this.left = left;this.right = right;this.max = Integer.MIN_VALUE;this.min = Integer.MAX_VALUE;this.sum = 0;}}int n;Node[] st;int[] nums;public void build(int index, int left, int right) {if (left == right) {st[index].sum = nums[left];st[index].max = nums[left];st[index].min = nums[left];return;}int mid = (right - left) / 2 + left;int leftIndex = index * 2;int rightIndex= index * 2 + 1;build(leftIndex, left, mid);build(rightIndex, mid+1, right);st[index].max = Math.max(st[leftIndex].max, st[rightIndex].max);st[index].min = Math.min(st[leftIndex].min, st[rightIndex].min);st[index].sum = st[leftIndex].sum + st[rightIndex].sum;}public void init(int N, int[] arr) {n = N;st = new Node[4 * n + 1];for (int i = 1; i <= 4 * n; i++) {st[i] = new Node();}nums = arr;}public int querySum(int left, int right) {return querySum(1, 0, n-1, left, right);}public int querySum(int index, int start, int end, int left, int right) {if (left > end || right < start) {return 0;} else if (left <= start && right >= end) {return st[index].sum;}int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;int leftSum = querySum(leftIndex, start, mid, left, right);int rightSum = querySum(rightIndex, mid + 1, end, left, right);return leftSum + rightSum;}public int queryMax(int left, int right) {return queryMax(1, 0, n-1, left, right);}public int queryMax(int index, int start, int end, int left, int right) {if (left > end || right < start) {return 0;} else if (left <= start && right >= end) {return st[index].sum;}int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;int leftMax = queryMax(leftIndex, start, mid, left, right);int rightMax = queryMax(rightIndex, mid + 1, end, left, right);return Math.max(leftMax, rightMax);}public int queryMin(int left, int right) {return queryMin(1, 0, n-1, left, right);}public int queryMin(int index, int start, int end, int left, int right) {if (left > end || right < start) {return Integer.MAX_VALUE;} else if (left <= start && right >= end) {return st[index].sum;}int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;int leftMin = queryMin(leftIndex, start, mid, left, right);int rightMin = queryMin(rightIndex, mid + 1, end, left, right);return Math.min(leftMin, rightMin);}public void update(int index, int start, int end, int updateIndex, int value) {if (start == end) {nums[updateIndex] = value;st[index].sum = value;st[index].max = value;st[index].min = value;return;} int mid = (start + end) / 2;int leftIndex = index * 2;int rightIndex = index * 2 + 1;if (updateIndex >= start && updateIndex <= mid) {update(leftIndex, start, mid, updateIndex, value);} else {update(rightIndex, mid + 1, end, updateIndex, value);}st[index].max = Math.max(st[leftIndex].max, st[index].max);st[index].min = Math.min(st[leftIndex].min, st[index].min);st[index].sum = st[leftIndex].sum + st[index].sum;}public void update(int index, int value) {nums[index] = value;update(1, 0, n - 1, index, value);}}